
|
|
ТЕМА 3. «Измерение связи между переменными, измеренными на различных шкалах»
3.1. Номинальная шкала. Измерение связи между дихотомическими переменными (таблица сопряженности 2x2). Для измерения связи между двумя дихотомическими переменными исходные данные представляются в виде таблицы сопряженности 2x2. Значениям дихотомической переменной можно присвоить произвольные числовые метки. Например, обозначать наличие некоторого свойства - единицей, а его отсутствие - нулем. Распределение двух таких переменных при условии, что они дихотомические, можно представить в виде таблицы сопряженности 2x2: Таблица 3.1. Таблица сопряженности 2x2
При измерении связи между номинальными переменными значения переменных не участвуют в расчетах. Различные меры связи в таких случаях базируются на частоте совместного появления определенной i- той категории (xi) одной переменной и определенной j- той категории (yi) другой переменной y. Для таблиц сопряженности 2x2 существуют специальные меры связей - коэффициент ассоциации и коэффициент контингенции. Коэффициент ассоциации (коэффициент Юла):
Коэффициент ассоциации обладает свойствами коэффициента корреляции, т.е. изменяется от -1 до + 1 . Если Q > 0, то связь положительна - с увеличением X признак Y увеличивается. Если Q < 0, то связь отрицательная. Коэффициент ассоциации равен нулю, если признаки независимы. Он равен единице, в случае полной связи признаков. Для проверки статистической значимости коэффициента ассоциации применяется t – критерий Стьюдента:
Коэффициент ассоциации считается статистически значимым, если tрасч. > tтабл.. Коэффициент контингенции:
Коэффициент контингенции также обладает свойствами коэффициента корреляции, т.е. изменяется в интервале от -1 до + 1. Он всегда меньше коэффициента ассоциации. Считается, что коэффициент контингенции является более достоверной мерой связи между дихотомическими переменными. Связь между двумя дихотомическими переменными признается подтвержденной, если Для оценки силы связи между переменными для таблиц сопряженности 2х2 также применяют τ - коэффициент Гудмена и Краскала:
Этот показатель является коэффициентом детерминации между X и Y, он изменяется в интервале от 0 до 1 . Пример 3.1. На основании выборочных данных о результатах исследования удовлетворенности заработной платой работников частных фирм и госпредприятий определить значения коэффициента ассоциации, коэффициента контингенции и коэффициента Гудмена и Краскала. Таблица 3.2. Таблица сопряженности между переменными « место работы респондента» и «удовлетворенность заработной платой»
Решение:
Вывод: Анализируя полученные результаты, можно отметить, что для данной выборки удовлетворенность работников заработной платой не зависит от места их работы, так как значения коэффициентов ассоциации и контингенции близки к 0. Коэффициент Гудмена и Краскала подтверждает этот вывод, показывая, что общая сопряженность рассматриваемых переменных только на 1,8% определяется местом работы респондентов. 3.2. Измерение связи между политомичными переменными (таблица сопряженности m x p ). Если переменные, измеренные на номинальной шкале, имеют более двух градаций, то они называются политомичными. Измерение связи между такого рода переменными осуществляется с помощью специальных показателей – коэффициентов взаимной сопряженности. К коэффициентам взаимной сопряженности относятся коэффициенты К.Пирсона, А.Чупрова, Г.Крамера. Коэффициенты взаимной сопряженности основаны на критерии хи – квадрат Пирсона. Эти меры связи принимают значения в интервале от 0 до +1. Равенство нулю любого из этих показателей означает отсутствие связи, т.е. полную независимость, а равенство единице - полную связь между переменными. Если переменная X имеет m – градаций, а переменная Y имеет p – градаций, то таблица сопряженности переменных X и Y размером m x p будет иметь следующий вид: Таблица 3.3. Таблица сопряженности между политомичными переменными размером m x p
Такая таблица используется для расчета различных коэффициентов взаимной сопряженности:
В представленных выше формулах
Считается, что коэффициент взаимной сопряженности Чупрова более строго оценивает тесноту связи, чем показатель Пирсона, так как коэффициент Пирсона не достигает максимального значения +1 даже при полной связи переменных, он лишь стремиться к этому значению при увеличении числа градаций переменных. Коэффициент взаимной сопряженности Чупрова характеризует долю фактической сопряженности переменных в их полной сопряженности, а квадрат этого показателя имеет смысл коэффициента детерминации. Коэффициент взаимной сопряженности Крамера рассчитывается только для неквадратных таблиц сопряженности и учитывает минимальную из величин: или число строк, или число столбцов таблицы сопряженности. Пример 3.2. Имеются данные о распределении студентов четырех факультетов экономического вуза, оценивавших степень сложности математических дисциплин, изучаемых в вузе: Таблица 3.4. Таблица сопряженности между переменными « место учебы респондента (факультет)» и «оценка степени сложности математических дисциплин, изучаемых в вузе».
Определить коэффициенты взаимной сопряженности Пирсона и Чупрова. Решение:
Вывод: Связь между оценкой студентами степени сложности математических дисциплин и местом их обучения (факультетом) слабая, т.е. такая оценка практически не зависит от факультета, на котором учатся студенты. Cуществуют модификации коэффициентов Пирсона и Чупрова, основанные на
Модифицированный коэффициент сопряженности Чупрова вычисляется следующим образом:
где k1 – число строк в таблице; k2 – число граф в таблице; n – число наблюдений. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (3.1)
(3.1) , где (3.2)
, где (3.2) (3.3)
(3.3) (3.4)
(3.4) > 0,5 или
> 0,5 или  > 0,3.
> 0,3. , (3.5)
, (3.5)
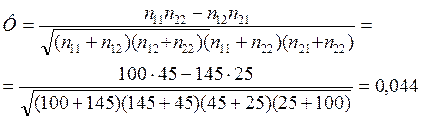

 …
…
…
…
…
…
…
…
…
…



 - коэффициент взаимной сопряженности Пирсона (3.6)
- коэффициент взаимной сопряженности Пирсона (3.6)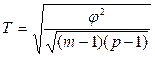 - коэффициент взаимной сопряженности Чупрова (3.7)
- коэффициент взаимной сопряженности Чупрова (3.7) - коэффициент взаимной сопряженности Крамера (3.8)
- коэффициент взаимной сопряженности Крамера (3.8)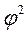 - показатель взаимной сопряженности, который вычисляется следующим образом:
- показатель взаимной сопряженности, который вычисляется следующим образом: или
или  (3.9)
(3.9)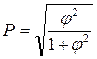 ;
; 






 -критерии Пирсона. Модифицированный коэффициент взаимной сопряженности Пирсона вычисляется по формуле:
-критерии Пирсона. Модифицированный коэффициент взаимной сопряженности Пирсона вычисляется по формуле: (3.10) , где
(3.10) , где  (3.11)
(3.11) , (3.12)
, (3.12)