
|
|
Определение оптических погрешностей линз (аберраций)Определение главного фокусного расстояния оптических систем.
Задание 1. Изучить по нижеследующему тексту способ нахождения фокусного расстояния собирающей оптической системы.
Главное фокусное расстояние собирающей линзы можно определить по формуле:
Оптическая сила тонкой линзы определяется формулой:
где F - фокусное расстояние линзы, f - расстояние от оптического центра до изображения, d-расстояние от оптического центра до предмета, R1 и R2 - радиусы кривизны линзы, n - показатель преломления линзы.
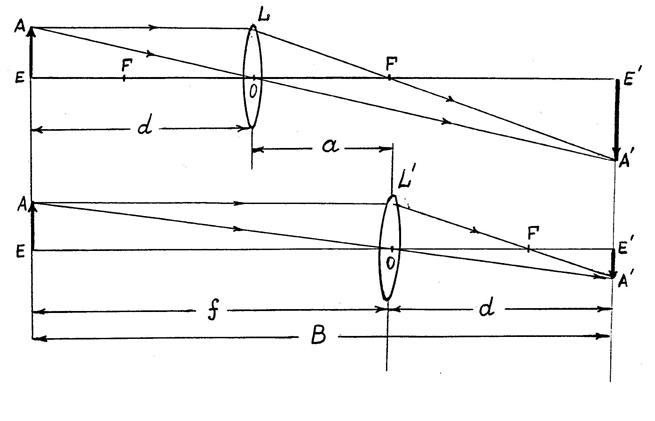
В формулах (1) и (2) F, F, d, R1 и R2 считаются положительными, если они отложены от линзы по ходу луча, к отрицательными - при обратном их направлении. Фокусное расстояние F линзы можно определить по формуле (1), зная d и F. Но на практике d и F определить трудно, так как оптический центр линзы L, в общем случае не совпадает с центром системы. Можно поступить следующим образом, Из формулы (1) видно, что величины d и F можно менять местами, причем эта формула не изменит свой вид. Практически это означает, что если на месте изображения установить предмет, то его изображение получится на том месте, где раньше стоял предмет. Это можно трактовать и так: если, получив, например, резкое обратное и увеличенное изображение предмета A'E' на экране (рис.1), измерить d и F, а затем, не трогая предмет и экран, передвинуть линзу L в L' так, чтобы расстояние между L' и A'E' равнялось d.. Тогда на экране мы увидим резкое, обратное и уменьшенное изображение предмета A'E' , которое будет находиться от L' как раз на расстоянии d.
Рис. 1 Таким образом, с помощью линзы можно получить два изображения: увеличенное, находящееся на расстоянии F от центра линзы, и уменьшенное - на расстоянии d, причем величины d и F связаны формулой (1). Обозначим величину, на которую сместился при этом центр линзы О, через a. Эту величину можно измерить перемещением любой точки линзы О, т.к. во время ее перемещения положение оптического центра внутри линзы не меняется. Последнее обстоятельство позволяет преодолеть указанную выше трудность, заменив измерение перемещения оптического центра О измерением перемещения какого-либо указателя на штативе этой линзы. Из рис. 1 видно, что B=f+d; a=f-d.Складывая или вычитая эти выражения,получим:
Принимая во внимание формулу (1), имеем:
•Задание 2. Определение фокусного расстояния собирающей линзы.
Установить на оптической скамье осветитель, экран и между ними изучаемую собирающую линзу. Выбрать базу В такую, чтобы на экране получались четкие изображения предмета (буквы "Т") при двух положениях линзы : один раз - увеличенное, другой раз -уменьшенное. При выбранной фиксированной базе перемещением линзы добиться резкого изображения предмета на экране. С помощью линейки замерить положение линзы относительно экрана или источника. Перемещать линзу при заданной базе до получения нового изображения предмета на экране. Снова измерить расстояние- от линзы до экрана или источника. По полученным измерениям а (рис. I} и по формуле (3) вычислить Р. Повторить вышеизложенное упражнение для одной линзы и одного значения Б не менее 3-х раз. Повторить упражнение для второй собирающей линзы. Результаты измерений усреднить, рассчитать фокусные расстояния обеих линз, оценить доверительные интервалы найденных значений F.
Задание 3. Определение фокусного расстояния системы двух собирающих линз. Составить систему из линз, фокусные расстояния которых были определены в задании 2. Определить фокусное расстояние системы способом, использованным в задании 2. Рассчитать F по формуле (3). Рассчитать оптическую силу системы.
Рассчитать Фс по формуле:
где Ф1 - оптическая сила первой линзы, Ф2 - оптическая сила второй линзы,
Рассчитать погрешности в определении Фс, сравнить значения, полученные с помощью формул (4) и (5). Сделать заключение о применимости формулы (5) для расчета оптической силы системы линз.
Задание 4. Определение фокусного расстояния рассеивающей линзы.
Рассеивающая линза не дает действительного изображения, поэтому определить ее фокусное расстояние методом, описанным в задании 2, нельзя. Сочетают рассеивающую линзу с фокусным расстоянием F2 с собирающей линзой с фокусным расстоянием F1 так, чтобы образованная ими система давала действительное изображение. Определить фокусное расстояние этой системы Fс, пересчитать фокусные расстояния Fс и F1 в оптические силы и по формуле (5) рассчитать оптическую силу и фокусное расстояние рассеивающей линзы.
Определение оптических погрешностей линз (аберраций) Задание 5. Изучить хроматическую аберрацию.
Показатель преломления n. вещества зависит от длины волны падающего света Погрешности линз, обусловленные зависимостью их главного фокусного расстояния от длины волны, называются хроматическими аберрациями. Устранение хроматической аберрации осуществляется комбинированием линз, благодаря чему различные цветные изображения совмещаются, давая в фокальной плоскости изображение, не имеющее радужной окраски. Проделаем рассчет для простейшего случая - системы двух линз с оптическими силами
Если линзы сложены вплотную, то оптическая сила системы равна
Хроматическая аберрация будет отсутствовать, если оптическая сила системы
или
Принципиально невозможно рассчитать систему, ахроматическую для всех длин волн. Возможно совмещение лишь двух разноцветных изображений, соответствующих двум выбранным длинам волн. Для визуальных приборов (действующих совместно с глазом наблюдателя) в качестве таких волн выбираются
для стекла второй
Записав формулы (6) и (7) для n1 и n2 , соответствующих произвольной длине волны, например,
Разделим обе части последнего уравнения на
или
где Задание 6. Изучить сферическую аберрацию.
Пусть диафрагма BB с небольшим круглым отверстием в центре (рис. 2) выделяет узкий пучок параксиальных лучей, исходящих из точки А.Заменим ее диафрагмой DD с кольцевым отверстием. Краевые лучи сильнее отклоняются в линзе, чем параксиальные, и при прежнем положении источника А его изображение окажется на меньшем расстоянии от линзы, чем в первом случае.
Величина Вопросы для самоподготовки 1. Понятие о тонкой линзе. Формула тонкой линзы. Для каких лучей применима формула линз? 2. Главное фокусное расстояние. Фокальная плоскость. Понятие оптической силы, светосилы, относительного отверстия. 3. Формула для главного фокусного расстояния линзы. 4. Типы линз. Перечислить все виды собирающих и рассеивающих линз. 5. Ход лучей в линзах. Понятие о действительном и мнимом изображениях. 6. Явление хроматической и сферической аберрации. Начертить ход лучей. Устранение хроматической и сферической аберрации. Литература 1. Ландсберг Г.С. Оптика. 2. Савельев И.В. Курс общей физики, ч.З. 3. Зисман Г.А., Тодес О.М. Курс общей физики, ч.З. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
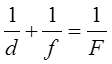 (1)
(1) (2)
(2)

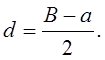
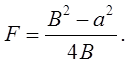 (3)
(3)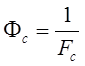 (4)
(4)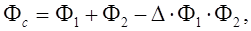 (5)
(5) - расстояние между центрами линз, образующих систему.
- расстояние между центрами линз, образующих систему.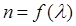 (дисперсия). Поскольку фокусное расстояние линзы зависит от показателя преломления (см, формулу (2)), то для каждого ив монохроматических лучей линза будет иметь свое фокусное расстояние. Но расстояния от оптического центра линзы до плоскости изображения и до предмета f и d связаны соотношением (1). Поэтому, если предмет, освещаемый белым светом, поместить на определенном расстоянии от линзы, то его резкое изображение будет находиться на различных расстояниях для различных монохроматических лучей. Передвигая экран, нельзя получить четкого изображения предмета. Оно будет всегда несколько размытым и окрашенным.
(дисперсия). Поскольку фокусное расстояние линзы зависит от показателя преломления (см, формулу (2)), то для каждого ив монохроматических лучей линза будет иметь свое фокусное расстояние. Но расстояния от оптического центра линзы до плоскости изображения и до предмета f и d связаны соотношением (1). Поэтому, если предмет, освещаемый белым светом, поместить на определенном расстоянии от линзы, то его резкое изображение будет находиться на различных расстояниях для различных монохроматических лучей. Передвигая экран, нельзя получить четкого изображения предмета. Оно будет всегда несколько размытым и окрашенным.
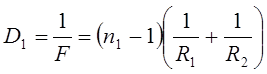
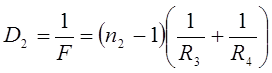 (7)
(7) (8)
(8)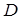 не зависит от длины волны, т.е.
не зависит от длины волны, т.е. 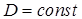 и
и  :
: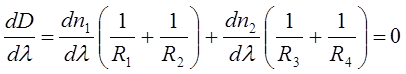
 (9)
(9)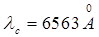 и
и  . Цвета, соответствующие этим волнам, - красный и зелено-голубой - являются дополнительными и при наложении дают ощущение белого цвета. Для стекла первой линзы можно записать
. Цвета, соответствующие этим волнам, - красный и зелено-голубой - являются дополнительными и при наложении дают ощущение белого цвета. Для стекла первой линзы можно записать ,
,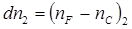
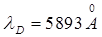 , и подставляя значения
, и подставляя значения 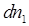 и
и 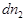 в (9), получим три уравнения:
в (9), получим три уравнения: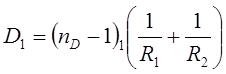 (10)
(10)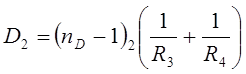 (11)
(11)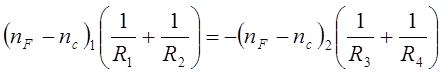 (12)
(12)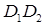 после преобразований получим:
после преобразований получим:
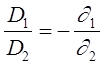 (13)
(13) и
и 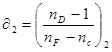 - коэффициенты дисперсии стекол линз. Формула (13) выражает условие ахроматизации двухпинзового объектива.Так как коэффициенты дисперсии имеют одинаковые знаки, то знак “–“ в формуле (13) показывает, что
- коэффициенты дисперсии стекол линз. Формула (13) выражает условие ахроматизации двухпинзового объектива.Так как коэффициенты дисперсии имеют одинаковые знаки, то знак “–“ в формуле (13) показывает, что 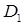 и
и  имеют разные знаки, т.е. ахроматизация может быть достигнута путем соединения собирающей линзы с рассеивающей. В данной работе изучается зависимость фокусного расстояния линзы отдлины волны падающего света. Для этого установить держатель для светофильтров. Из формулы (1) видно, что если оставлять постоянным расстояние , d то
имеют разные знаки, т.е. ахроматизация может быть достигнута путем соединения собирающей линзы с рассеивающей. В данной работе изучается зависимость фокусного расстояния линзы отдлины волны падающего света. Для этого установить держатель для светофильтров. Из формулы (1) видно, что если оставлять постоянным расстояние , d то 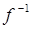 и
и 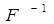 будут пропорциональны друг другу. Это обстоятельство позволяет упростить измерения и расчеты в данном задании. Так как нас интересует характер зависимости
будут пропорциональны друг другу. Это обстоятельство позволяет упростить измерения и расчеты в данном задании. Так как нас интересует характер зависимости  от
от 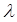 , то вместо
, то вместо  можно измерять пропорциональную ему величину
можно измерять пропорциональную ему величину 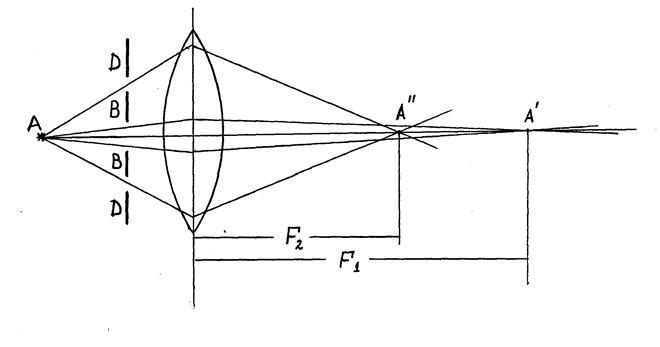 Рис. 2
Рис. 2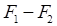 называется продольной сферической аберрацией. Она обусловлена тем, что различные кольцевые волны имеют различные фокусные расстояния и, следовательно, различные значения f при заданном d. Вследствие сферической аберрации изображение предмета получается размытым. Действительно, лучи от источника А, преломленные различными кольцевыми зонами линзы, пересекают главную оптическую ось в различных точках (точки А' и А" ) и, в каком бы месте ни поместили экран СC, точка А изобразится в виде размытого кружка. В одном из положений между А' и А" диаметр светового пятна будет наименьшим, что соответствует наиболее отчетливому изображению.Поставить большую собирающую линзу. Передвигая экран СС, добиться резкого изображения предмета. Установить диафрагму с кольцевым вырезом. Передвигая экран, снова получить наибольшее четкое изображение предмета. Повторить эксперимент для различных кольцевых диафрагм, измеряя соответствующие значения f. Построить график зависимости
называется продольной сферической аберрацией. Она обусловлена тем, что различные кольцевые волны имеют различные фокусные расстояния и, следовательно, различные значения f при заданном d. Вследствие сферической аберрации изображение предмета получается размытым. Действительно, лучи от источника А, преломленные различными кольцевыми зонами линзы, пересекают главную оптическую ось в различных точках (точки А' и А" ) и, в каком бы месте ни поместили экран СC, точка А изобразится в виде размытого кружка. В одном из положений между А' и А" диаметр светового пятна будет наименьшим, что соответствует наиболее отчетливому изображению.Поставить большую собирающую линзу. Передвигая экран СС, добиться резкого изображения предмета. Установить диафрагму с кольцевым вырезом. Передвигая экран, снова получить наибольшее четкое изображение предмета. Повторить эксперимент для различных кольцевых диафрагм, измеряя соответствующие значения f. Построить график зависимости 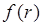 , где r - радиус диафрагмы. Графики строить только на миллиметровой бумаге. При обсуждении результатов работы обратить внимание на ход зависимостей
, где r - радиус диафрагмы. Графики строить только на миллиметровой бумаге. При обсуждении результатов работы обратить внимание на ход зависимостей  и
и