
|
|
Геометрическое распределениеЛЕКЦИЯ 8 Распределения вероятностей дискретных случайных величин. Биномиальное распределение. Распределение Пуассона. Геометрическое распределение. Производящая функция. 6. РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ Биномиальное распределение Пусть производится n независимых испытаний, в каждом из которых событие A может либо появится, либо не появится. Вероятность p появления события A во всех испытаниях постоянна и не изменяется от испытания к испытанию. Рассмотрим в качестве случайной величины X число появлений события A в этих испытаниях. Формула, позволяющая найти вероятность появления события A
Распределение вероятностей, определяемое формулой Бернулли, называется биномиальным. Этот закон назван "биномиальным" потому, что правую часть можно рассматривать как общий член разложения бинома Ньютона
Запишем биномиальный закон в виде таблицы
Найдем числовые характеристики этого распределения. По определению математического ожидания для ДСВ имеем
Запишем равенство, являющееся бином Ньютона
и продифференцируем его по p. В результате получим
Умножим левую и правую часть на p:
Учитывая, что p+q=1, имеем
Итак, математическое ожидание числа появлений событий в n независимых испытаниях равно произведению числа испытаний n на вероятность p появления события в каждом испытании. Дисперсию вычислим по формуле
Для этого найдем
Предварительно продифференцируем формулу бинома Ньютона два раза по p:
и умножим обе части равенства на p2:
находим
Следовательно,
Итак, дисперсия биномиального распределения равна
Данные результаты можно получить и из чисто качественных рассуждений. Общее число X появлений события A во всех испытаниях складываются из числа появлений события в отдельных испытаниях. Поэтому если X1 – число появлений события в первом испытании, X2 – во втором и т.д., то общее число появлений события A во всех испытаниях равно X=X1+X2+…+Xn. По свойству математического ожидания:
Каждое из слагаемых правой части равенства есть математическое ожидание числа событий в одном испытании, которое равно вероятности события. Таким образом,
По свойству дисперсии:
Так как
Воспользовавшись понятием начальных и центральных моментов, можно получить формулы для асимметрии и эксцесса:
Число m0 наступлений события называется наивероятнейшим, если вероятность наступления события данное число раз в этой серии испытаний наибольшая (максимум в многоугольнике распределения). Для биномиального распределения
Замечание. Данное неравенство можно доказать, используя рекуррентную формулу для биномиальных вероятностей:
Пример 6.1. Доля изделий высшего сорта на данном предприятии составляет 31%. Чему равно математического ожидание и дисперсия, также наивероятнейшее число изделий высшего сорта в случайно отобранной партии из 75 изделий? Решение. Поскольку p=0,31, q=0,69, n=75, то M[X] = np = 75×0,31 = 23,25; D[X] = npq = 75×0,31×0,69 = 16,04. Для нахождения наивероятнейшего числа m0, составим двойное неравенство
Отсюда следует, что m0 = 23. Распределение Пуассона Как было уже отмечено, биномиальное распределение приближается к нормальному при n®¥. Однако это не имеет места, если наряду с увеличением n одна из величин p или q стремится к нулю. В этом случае имеет место асимптотическая формула Пуассона, т.е. при n®¥, p®0
где l=np. Эта формула определяет закон распределения Пуассона, который имеет самостоятельное значение, а не только как частный случай биномиального распределения. В отличие от биномиального распределения здесь случайная величина k может принимать бесконечное множество значений: k=0,1,2,… Закон Пуассона описывает число событий k, происходящих за одинаковые промежутки времени при условии, что события происходят независимо друг от друга с постоянной средней интенсивностью, которая характеризуется параметром l. Многоугольник распределения Пуассона показан на рис. 6.2. Отметим, что при больших l рас Примерами ситуаций, в которых возникает распределение Пуассона, могут служить распределения: 1) числа определенных микробов в единице объема; 2) числа вылетевших электронов с накаленного катода за единицу времени; 3) числа a-частиц, испускаемых радиоактивным источником за определенных промежуток времени; 4) числа вызовов, поступающих на телефонную станцию за определенное время суток и т.д. Запишем закон Пуассона в виде таблицы
Проверим, что сумма всех вероятностей равна единице:
Найдем числовые характеристики этого распределения. По определению математического ожидания для ДСВ имеем
Отметим, что в последней сумме суммирование начинается с k=1, т.к. первый член суммы, соответствующий k=0, равен нулю. Для нахождения дисперсии найдем предварительно математического ожидание квадрата случайной:
Тогда
Таким образом, математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру этого распределения
В этом состоит отличительная особенность распределения Пуассона. Так, если на основании опытных данных было получено, что математическое ожидание и дисперсия некоторой величины близки между собой, то есть основания предполагать, что данная случайная величина распределена в соответствии с законом Пуассона. Воспользовавшись понятием начальных и центральных моментов, можно показать, что для распределения Пуассона коэффициент асимметрии и эксцесс равны:
Поскольку параметр l всегда положителен, то у распределения Пуассона всегда положительная асимметрия и эксцесс. Покажем теперь, что формулу Пуассона можно рассматривать как математическую модель простейшего потока событий. Потоком событий называют последовательность событий, которые наступают в случайные моменты времени. Поток называется простейшим, если он обладает свойствами стационарности, отсутствия последействия и ординарности. Интенсивностью потока l называют среднее число событий, которые появляются в единицу времени. Если постоянная интенсивности потока l известна, то вероятность появления k событий простейшего потока за время t определяется формулой Пуассона:
Эта формула отражает все свойства простейшего потока. Более того, любой простейший поток описывается формулой Пуассона, поэтому простейшие потоки часто называют пуассоновскими. Свойство стационарности состоит в том, что вероятность появления k событий в любом промежутке времени зависит только от числа k и от длительности t промежутка времени и не зависит от начала его отсчета. Другими словами, если поток обладает свойством стационарности, то вероятность появления k событий за промежуток времени t есть функция, зависящая только от k и от t. В случае простейшего потока из формулы Пуассона (6.10) следует, что вероятность k событий за время t, при заданной интенсивности является функцией только двух аргументов: k и t, что характеризует свойство стационарности. Свойство отсутствия последействия состоит в том, что вероятность появления k событий в любом промежутке времени зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка. Другими словами, предыстория потока не влияет на вероятности появления событий в ближайшем будущем. В случае простейшего потока в формуле Пуассона (6.10) не используется информация о появлении событий до начала рассматриваемого промежутка времени, что характеризует свойство отсутствия последействия. Свойство ординарности состоит в том, что появление двух или более событий за малый промежуток времени практически невозможно. Другими словами, вероятность появление более одного события за малый промежуток времени пренебрежимо мала по сравнению с вероятностью появления только одного события. Покажем, что формула Пуассона (6.10) отражает свойство ординарности. Положив k=0 и k=1, найдем соответственно вероятности не появления событий и появления одного события:
Следовательно, вероятность появления более одного события равна
Используя разложение функции
Сравнивая Pt(1) и Pt(k>1), заключаем, что при малых значениях t вероятность появления более одного события пренебрежимо мала по сравнению с вероятностью наступления одного события, что характеризует свойство ординарности. Пример 6.2. В наблюдениях Резерфорда и Гейгера радиоактивное вещество за промежуток времени 7,5 сек испускало в среднем 3,87 a-частицы. Найти вероятность того, что за 1 сек это вещество испустит хотя бы одну частицу. Решение. Как мы уже отмечали, распределение числа a-частиц, испускаемых радиоактивным источником за определенных промежуток времени описывается формулой Пуассона, т.е. образует простейший поток событий. Поскольку интенсивность испускания a-частиц за 1 сек равно
то формула Пуассона (6.10) примет вид
Таким образом, вероятность того, что за t=1 сек вещество испустит хотя бы одну частицу будет равно
Геометрическое распределение Пусть производится стрельба по заданной мишени до первого попадания, при этом вероятность p попадания в цель в каждом выстреле одна и та же и не зависит от результатов предыдущих выстрелов. Другими словами, в рассматриваемом опыте осуществляется схема Бернулли. В качестве случайной величины X будем рассматривать число произведенных выстрелов. Очевидно, что возможными значениями случайной величины X являются натуральные числа: x1=1, x2=2, … тогда вероятность того, что понадобится k выстрелов будет равна
Полагая в этой формуле k=1,2, … получим геометрическую прогрессию с первым членом p и множителем q:
По этой причине распределение, определяемое формулой (6.11) называется геометрическим. Используя формулу суммы бесконечно убывающей геометрической прогрессии, легко убедится, что
Найдем числовые характеристики геометрического распределения. По определению математического ожидания для ДСВ имеем
Дисперсию вычислим по формуле
Для этого найдем
Следовательно,
Итак, математическое ожидание и дисперсия геометрического распределения равна
6.4.* Производящая функция При решении задач, связанных с ДСВ, часто используются методы комбинаторики. Одним из наиболее развитых теоретических методов комбинаторного анализа является метод производящих функций, который является одним из самых сильных методов и в применениях. Кратко познакомимся с ним. Если случайная величина x принимает только целые неотрицательные значения, т.е.
то производящей функцией распределения вероятностей случайной величины x называется функция
где z – действительная или комплексная переменная. Отметим, что между множеством производящих функций jx(x) и множеством распределений {P(x=k)} существует взаимно однозначное соответствие. Пусть случайная величина x имеет биномиальное распределение
Тогда, используя формулу бинома Ньютона, получим
т.е. производящая функция биномиального распределения имеет вид
Добавление. Производящая функция распределения Пуассона
имеет вид
Производящая функция геометрического распределения
имеет вид
При помощи производящих функций удобно находить основные числовые характеристики ДСВ. Например, первый и второй начальный моменты связаны с производящей функцией следующими равенствами:
Метод производящих функций часто бывает удобен тем, что в некоторых случаях функцию распределения ДСВ очень трудно определить, тогда как производящую функцию порой легко найти. Например, рассмотрим схему последовательных независимых испытаний Бернулли, но внесем в нее одно изменение. Пусть вероятность осуществления события A от испытания к испытанию меняется. Это означает, что формула Бернулли для такой схемы становится неприменимой. Задача нахождения функции распределения в таком случае представляет значительные трудности. Однако для данной схемы легко находится производящая функция, а, следовательно, легко находятся и соответствующие числовые характеристики. Широкое применение производящих функций основано на том, что изучение сумм случайных величин можно заменить изучением произведений соответствующих производящих функций. Так, если x1, x2, …, xn независимы, то
Пусть pk=Pk(A) – вероятность "успеха" в k-м испытании в схеме Бернулли (соответственно, qk=1–pk – вероятность "неуспеха" в k-м испытании). Тогда, в соответствие с формулой (6.19), производящая функция будет иметь вид
Пользуясь данной производящей функцией, можем написать
Здесь учтено, что pk+qk=1. Теперь по формуле (6.1) найдем второй начальный момент. Для этого предварительно вычислим
Тогда
В частном случае p1=p2=…=pn=p (т.е. в случае биномиального распределения) из полученных формул следует, что Mx=np, Dx=npq.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . (6.1)
. (6.1) .
.
 .
. .
. .
. .
. (6.2)
(6.2) .
. .
.



 . (6.3)
. (6.3) .
. .
. .
. , а математическое ожидание случайной величины
, а математическое ожидание случайной величины 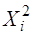 , которое может принимать только два значения, а именно 12 с вероятностью p и 02 с вероятностью q, то
, которое может принимать только два значения, а именно 12 с вероятностью p и 02 с вероятностью q, то  . Таким образом,
. Таким образом,  В результате, получаем
В результате, получаем .
.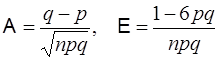 . (6.4)
. (6.4) Многоугольник биномиального распределения имеет следующий вид (см. рис. 6.1). Вероятность Pn(k) сначала возрастает при увеличении k, достигает наибольшего значения и далее начинает убывать. Биномиальное распределение асимметрично, за исключением случая p=0,5. Отметим, что при большом числе испытаний n биномиальное распределение весьма близко к нормальному. (Обоснование этого предложения связано с локальной теоремой Муавра-Лапласа.)
Многоугольник биномиального распределения имеет следующий вид (см. рис. 6.1). Вероятность Pn(k) сначала возрастает при увеличении k, достигает наибольшего значения и далее начинает убывать. Биномиальное распределение асимметрично, за исключением случая p=0,5. Отметим, что при большом числе испытаний n биномиальное распределение весьма близко к нормальному. (Обоснование этого предложения связано с локальной теоремой Муавра-Лапласа.) . (6.5)
. (6.5)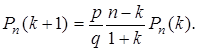 (6.6)
(6.6) .
. , (6.7)
, (6.7) пределение Пуассона приближается к нормальному. Поэтому распределение Пуассона применяется, как правило, в тех случаях, когда l имеет порядок единицы, при этом число испытаний n должно быть велико, а вероятность появления события p в каждом испытании мала. В связи с этим закон Пуассона часто называют еще законом распределения редких явлений.
пределение Пуассона приближается к нормальному. Поэтому распределение Пуассона применяется, как правило, в тех случаях, когда l имеет порядок единицы, при этом число испытаний n должно быть велико, а вероятность появления события p в каждом испытании мала. В связи с этим закон Пуассона часто называют еще законом распределения редких явлений.






 .
.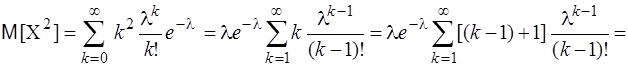


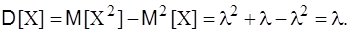
 . (6.8)
. (6.8) . (6.9)
. (6.9) . (6.10)
. (6.10)
 .
. в ряд Маклорена, после элементарных преобразований получим
в ряд Маклорена, после элементарных преобразований получим .
. ,
,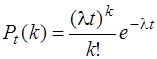
 .
. . (6.11)
. (6.11) .
. .
.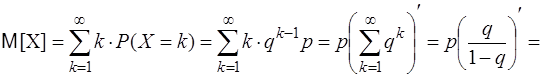
 .
.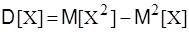 .
.

 .
. .
. . (6.12)
. (6.12) ,
, , (6.13)
, (6.13) .
. ,
, . (6.14)
. (6.14)
 . (6.15)
. (6.15)
 . (6.16)
. (6.16) , (6.17)
, (6.17) . (6.18)
. (6.18) . (6.19)
. (6.19) . (6.20)
. (6.20) .
. .
. и
и  .
.