
|
|
Дискретные двумерные случайные величины12 ЛЕКЦИЯ 11 Системы случайных величин. Функция распределения двумерной случайной величины. Числовые характеристики двумерной случайной величины. Коэффициент корреляции. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН 9.1. Функция распределения двумерной До сих пор мы рассматривали случайные величины, возможные значения которых определялись одним числом. Такие величины называются одномерными. Например, число очков, которое может выпасть при бросании игральной кости, является случайной величиной; расстояние от орудия до места падения снаряда – непрерывной одномерной случайной величиной. Кроме таких одномерных величин, часто приходится рассматривать одновременно системы из двух, трех и большего числа случайных величин. Например, координаты точки попадания при стрельбе характеризуются двумя случайными величинами: абсциссой и ординатой; осколок, образовавшийся при разрыве снаряда, характеризуется рядом случайных величин: весом, размерами, начальной скоростью, направлением полета и т.д. При рассмотрении вопросов, связанных с системами случайных величин, удобно пользоваться геометрической интерпретацией системы. Например, систему двух случайных величин {X1, X2} можно изобразить случайной точкой на плоскости с координатами X1 и X2. Часто вместо образа случайной точки для геометрической интерпретации пользуются образом случайного вектора
В дальнейшем мы будем в зависимости от удобства пользоваться как одной, так и другой интерпретацией. Изложение мы проводить в основном для случая двумерных величин. Общий n-мерный случай рассматривается совершенно аналогично. Функцией распределения F(x, y) двумерной случайной величины {X, Y} называется вероятность совместного выполнения двух неравенств: X<x, Y<y:
Рассмотрим свойства двумерной функции распределения, которые аналогичны свойствам функции распределения одномерной случайной величины. Так как F(x,y) – вероятность, то очевидно следующее свойство: Свойство 1. Функция распределения – величина неотрицательная, не превышающая единицы:
Свойство 2. Функция распределения есть неубывающая функция по каждому аргументу:
Эти неравенства следуют из свойств одномерных функций распределения, которые получаются из F(x,y) при фиксировании y и x соответственно. Свойство 3. Если хотя бы один из аргументов стремится к –¥, то функция распределения стремится к нулю:
Эти равенства следуют из того, что события {X1<–¥} и {X2<–¥} есть события невозможные. Свойство 4. Если оба аргумента стремятся к +¥, то функция распределения стремится к единице:
Это равенство следуют из того, что события {X1<+¥} и {X2<+¥} есть события достоверные. Свойство 5. Если один из аргументов обращается в +¥, то функция распределения F(x,y) становится функцией распределения, соответствующей другому аргументу:
Первое равенство следуют из того, что события {Y<+¥} есть событие достоверное, тогда F(x,+¥) определяет вероятность события {X<x}, т.е. представляет собой функцию распределения составляющей X. Аналогично обосновывается второе равенство. Зная функцию распределения F(x,y) можно найти вероятность попадания случайной величины {X, Y} в прямоугольник со сторонами R=(x1£X<x2, y1£Y<y2):
Дискретные двумерные случайные величины Двумерная случайная величина {X,Y} называется дискретной, если каждая из случайных величин X и Y является дискретной. Ясно, что если дискретная величина X может принимать только значения x1,…,xn, а случайная величина Y – значения y1,…,yn, то двумерный случайный вектор {X,Y} может принимать только пары значений (xi,yj). Обычно системы двух ДСВ описывается матрицей распределения, т.е. прямоугольной таблицей, в которой записаны все вероятности pij того, что двумерная ДСВ примет значение (xi,yj).
Сумма всех вероятностей pij , стоящих в матрице, равна единице как сумма вероятностей полной группы несовместных событий:
Зная матрицу распределения системы двух ДСВ легко найти законы распределения отдельных случайных величин, входящих в систему:
Пример 9.1. Двумерная дискретная величина {X,Y} задана законом распределения:
Найти законы распределения составляющих X и Y. Решение. Суммируя вероятности в i-й строке, находим P(X=xi)=pi, (i=1,2,3,4): P(X=2)=0,3+0,15+0,05=0,50, P(X=3)=0,15+0,10+0,05=0,30, P(X=4)=0,05+0,05+0,05=0,15, P(X=5)=0,05. Проверка: 0,5+0,3+0,15+0,05=1. Суммируя вероятности в k-м столбце, находим P(Y=yj)=qj, (j=1,2,3): P(Y=2)=0,3+0,15+0,05+0,05=0,55, P(Y=3)=0,15+0,10+0,05=0,30, P(Y=4)=0,05+0,05+0,05=0,15. Проверка: 0,55+0,3+0,15=1. Таким образом, законы распределения X и Y имеют вид: 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
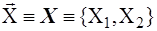 .
. . (9.1)
. (9.1)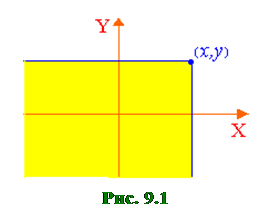 Двумерная функция распределения, по определению, представляет собой не что иное, как вероятность попадания точки с координатами {X, Y} в бесконечный квадрант с вершиной в точке (x,y), лежащий левее и ниже ее (см. рис. 9.1).
Двумерная функция распределения, по определению, представляет собой не что иное, как вероятность попадания точки с координатами {X, Y} в бесконечный квадрант с вершиной в точке (x,y), лежащий левее и ниже ее (см. рис. 9.1). .
. ,
, .
. .
. .
. ,
, .
.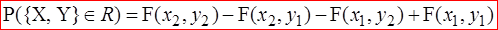 . (9.2)
. (9.2) Действительно, вероятность попадания в прямоугольник R равна вероятности попадания в квадрант (x2,y2) минус вероятность попадания в квадрант (x1,y2) минус вероятность попадания в квадрант (x2,y1) плюс вероятность попадания в квадрант (x1,y1) (так как мы дважды вычли вероятность попадания в этот квадрант).
Действительно, вероятность попадания в прямоугольник R равна вероятности попадания в квадрант (x2,y2) минус вероятность попадания в квадрант (x1,y2) минус вероятность попадания в квадрант (x2,y1) плюс вероятность попадания в квадрант (x1,y1) (так как мы дважды вычли вероятность попадания в этот квадрант). Y
X
Y
X
 .
.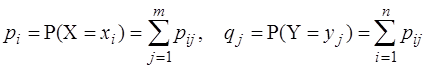 .
. Y
X
Y
X