Интегральный признак сходимости Коши
Сумма ряда
Определение суммы ряда.
Выражение вида

называем рядом;  -- n-ый член ряда (1). Сумма -- n-ый член ряда (1). Сумма  называется n-ой частичной суммой ряда (1). называется n-ой частичной суммой ряда (1).
Определение 1. Суммой ряда (1) называется предел частичных сумм, если  . Итак, сумма ряда (1) есть число . Итак, сумма ряда (1) есть число

т.е. такое число, что для любого  найдется натуральное найдется натуральное 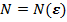 начиная с которого, т.е. для любого начиная с которого, т.е. для любого  выполняется неравенство выполняется неравенство

Если существует предел (2), то ряд (1) называется сходящимся. В противном случае, ряд (1) называется расходящимся.
Ряд  называется n-ым остатком ряда (1) и обозначается называется n-ым остатком ряда (1) и обозначается  . Таким образом, неравенство (3) эквиваленто следующему неравенству . Таким образом, неравенство (3) эквиваленто следующему неравенству

Задача о вычислении суммы ряда (1) с точностью 𝜺 сводится к поиску такого натурального числа n, что  . Тогда . Тогда  с точностью с точностью 
Примеры. а) 0+0+0+… - сходящийся ряд;
б) 𝜺 +𝜺 +𝜺 +… - расходящийся ряд, какое бы малое положительное число 𝜺 мы не взяли;
в) конечная сумма  превращается в сходящийся ряд, если положить превращается в сходящийся ряд, если положить  при при  ; при этом сумма данного ряда равна исходной сумме; ; при этом сумма данного ряда равна исходной сумме;
г) 1+1/2+1/4+1/8+… сходится к числу 2, ибо  имеет пределом 2 при n→ ∞ ; имеет пределом 2 при n→ ∞ ;
д)  . .
Критерий Коши для ряда.Ряд (1) сходится в том и только том случае, если для любого 𝜺 >0 найдется номер N такой, что для любых m≥ n≥ N имеет место неравенство

Предложение. Дописывание или отбрасывание конечного числа слагаемых ряда не влияет на его сходимость (но влияет на его сумму).
Необходимый признак сходимости.
Теорема. Если ряд (1) сходится то n-ый член стремится к 0 .
Доказательство.  . □ . □
Пример. Гармоническим рядом называется ряд

Для этого ряда  но этот ряд расходится, как показывает далее интегральный признак Коши. но этот ряд расходится, как показывает далее интегральный признак Коши.
Геометрическая прогрессия
- это ряд вида

Число q называется знаменателем геометрической прогрессии.
Теорема 2. Пусть  . Тогда геометрическая прогрессия сходится тогда и только тогда, когда |q|<1. В этом случае сумма геометрической прогрессии равна . Тогда геометрическая прогрессия сходится тогда и только тогда, когда |q|<1. В этом случае сумма геометрической прогрессии равна  . .
Утверждение следует из равенства  □ □
Арифметические операции с рядами.
Определим сумму двух рядов  и и  как ряд с n-ым слагаемым как ряд с n-ым слагаемым  . Произведение ряда (1) на число l - это ряд . Произведение ряда (1) на число l - это ряд  . .
Теорема. Если ряды  и и  сходятся соответственно к s и t, то сумма этих рядов сходится к числу s+t, а произведение ряда сходятся соответственно к s и t, то сумма этих рядов сходится к числу s+t, а произведение ряда  на число l сходится к на число l сходится к  . .
Доказательство вытекает из соответствующих свойств предела
Примеры. Найдем сумму ряда

Заметим, что  , и поэтому , и поэтому  , т.е. 1 - сумма ряда (1). , т.е. 1 - сумма ряда (1).
Найдем сумму ряда  . Для этого разложим n-ое слагаемое следующим образом: . Для этого разложим n-ое слагаемое следующим образом:

Тогда из результата предыдущего примера вытекает, что сумма нашего ряда равна

Теорема сравнения.
Лемма 1. Пусть дан ряд с неотрицательными слагаемыми. Тогда этот ряд сходится тогда и только тогда, когда его частичные суммы ограничены.
Доказательство. Если  -- ряд с неотрицательными слагаемыми, то -- ряд с неотрицательными слагаемыми, то  , частичные суммы ряда образуют возрастающую последовательность. Если она, к тому же еще и ограничена, то существование предела , частичные суммы ряда образуют возрастающую последовательность. Если она, к тому же еще и ограничена, то существование предела  , т.е. сходимость ряда , т.е. сходимость ряда  следует из теоремы о пределе монотонной ограниченной последовательности (см. главу «Введение в анализ» ). Обратное утверждение вытекает из ограниченности последовательности, имеющей предел. □ следует из теоремы о пределе монотонной ограниченной последовательности (см. главу «Введение в анализ» ). Обратное утверждение вытекает из ограниченности последовательности, имеющей предел. □
Теорема сравнения. Пусть  для любого натурального n начиная с некоторого номера. Если ряд для любого натурального n начиная с некоторого номера. Если ряд  сходится, то и ряд сходится, то и ряд  сходится. Если же ряд сходится. Если же ряд  расходится, то ряд расходится, то ряд  также расходится. также расходится.
Доказательство. Отбрасывая, если надо, первые несколько членов рядов  и и  , сводим доказательство к случаю, когда неравенство , сводим доказательство к случаю, когда неравенство  выполняется для всех выполняется для всех  Обозначим через Обозначим через  частичные суммы ряда частичные суммы ряда  , а через , а через  обозначим частичные суммы ряда обозначим частичные суммы ряда  . Тогда . Тогда  . Сходимость ряда . Сходимость ряда  влечет ограниченность сверху последовательности влечет ограниченность сверху последовательности  , что в свою очередь дает ограниченность последовательности , что в свою очередь дает ограниченность последовательности  . По лемме получаем сходимость ряда . По лемме получаем сходимость ряда  . Наоборот, если ряд . Наоборот, если ряд  расходится, то ряд расходится, то ряд  не может сходится, ибо в противном случае сходился бы и ряд не может сходится, ибо в противном случае сходился бы и ряд  , что противоречит доказанному выше. □ , что противоречит доказанному выше. □
Следствие. Пусть  для любого натурального n, начиная с некоторого номера, и существует отличный от 0 предел отношения для любого натурального n, начиная с некоторого номера, и существует отличный от 0 предел отношения  . Тогда ряды . Тогда ряды  и и  ведут себя одинаково в смысле сходимости (либо оба сходятся, либо оба расходятся). ведут себя одинаково в смысле сходимости (либо оба сходятся, либо оба расходятся).
Доказательство. Пусть  . По условию . По условию  . Предположим, что ряд . Предположим, что ряд  сходится. Выберем сходится. Выберем  . Тогда . Тогда  начиная с некоторого начиная с некоторого  . Отсюда вытекает неравенство . Отсюда вытекает неравенство  . Из сходимости ряда . Из сходимости ряда  следует сходимость ряда следует сходимость ряда  (см. «арифметические операции с рядами»). По теореме сравнения получаем тогда, что и ряд (см. «арифметические операции с рядами»). По теореме сравнения получаем тогда, что и ряд  сходится. Предположим теперь, что ряд сходится. Предположим теперь, что ряд  сходится. Так как сходится. Так как  (именно в этом месте нужно учесть, что (именно в этом месте нужно учесть, что  ), то мы можем в рассуждениях выше заменить ), то мы можем в рассуждениях выше заменить  на на  , а , а  на на  и и  на на  . Получаем сходимость ряда . Получаем сходимость ряда  . □ . □
Интегральный признак сходимости Коши
Теорема (интегральный признак сходимости Коши). Пусть  - монотонно убывающая, непрерывная и неотрицательная функция при - монотонно убывающая, непрерывная и неотрицательная функция при  . Положим . Положим  для натуральных n. Тогда ряд для натуральных n. Тогда ряд  и интеграл и интеграл  ведут себя одинаково в смысле сходимости. При этом имеет место следующая оценка остатка ряда ведут себя одинаково в смысле сходимости. При этом имеет место следующая оценка остатка ряда  : :

Доказательство по сути вытекает из рисунка. Имеем  (*). Если (*). Если  ряд ряд  сходится, то и ряд сходится, то и ряд  сходится по теореме сравнения. Отсюда следует, что интеграл сходится по теореме сравнения. Отсюда следует, что интеграл 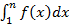 имеет предел при имеет предел при  . Из этого вытекает (с учетом монотонности функции . Из этого вытекает (с учетом монотонности функции  ), что существует предел ), что существует предел  . Это доказывает сходимость интеграла . Это доказывает сходимость интеграла  . Наоборот, если последний интеграл сходится и равен . Наоборот, если последний интеграл сходится и равен 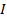 , то , то  для любого для любого  . Отсюда и из неравенств (*) следует ограниченность частичных сумм ряда. По лемме 1 из параграфа «теорема сравнения» вытекает сходимость ряда . Отсюда и из неравенств (*) следует ограниченность частичных сумм ряда. По лемме 1 из параграфа «теорема сравнения» вытекает сходимость ряда  . Оценка остатка ряда . Оценка остатка ряда  следует из неравенства (*): следует из неравенства (*):
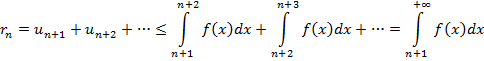
Следствие. Ряд  сходится тогда и только тогда, когда сходится тогда и только тогда, когда  . В частности, гармонический ряд расходится. . В частности, гармонический ряд расходится.
Доказательство. Применим теорему, беря в качестве функции  . Если . Если  , то , то

в силу того, что 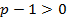 . Если . Если  , то , то

ибо  неограниченно возрастающая функция. В случае неограниченно возрастающая функция. В случае  из неравенства из неравенства  и уже доказанной расходимости гармонического ряда и уже доказанной расходимости гармонического ряда  вытекает расходимость ряда вытекает расходимость ряда  (применяем теорему сравнения). □ (применяем теорему сравнения). □
Пример. Ряд 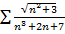 сходится, ибо сходится, ибо  . Так как ряд . Так как ряд  сходится (здесь сходится (здесь  ), то по следствию теоремы сравнения получаем сходимость исходного ряда. ), то по следствию теоремы сравнения получаем сходимость исходного ряда.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|



 -- n-ый член ряда (1). Сумма
-- n-ый член ряда (1). Сумма  называется n-ой частичной суммой ряда (1).
называется n-ой частичной суммой ряда (1). . Итак, сумма ряда (1) есть число
. Итак, сумма ряда (1) есть число
 найдется натуральное
найдется натуральное 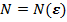 начиная с которого, т.е. для любого
начиная с которого, т.е. для любого  выполняется неравенство
выполняется неравенство
 называется n-ым остатком ряда (1) и обозначается
называется n-ым остатком ряда (1) и обозначается  . Таким образом, неравенство (3) эквиваленто следующему неравенству
. Таким образом, неравенство (3) эквиваленто следующему неравенству
 . Тогда
. Тогда  с точностью
с точностью 
 превращается в сходящийся ряд, если положить
превращается в сходящийся ряд, если положить  при
при  ; при этом сумма данного ряда равна исходной сумме;
; при этом сумма данного ряда равна исходной сумме; имеет пределом 2 при n→ ∞ ;
имеет пределом 2 при n→ ∞ ; .
.
 . □
. □ 
 но этот ряд расходится, как показывает далее интегральный признак Коши.
но этот ряд расходится, как показывает далее интегральный признак Коши.
 . Тогда геометрическая прогрессия сходится тогда и только тогда, когда |q|<1. В этом случае сумма геометрической прогрессии равна
. Тогда геометрическая прогрессия сходится тогда и только тогда, когда |q|<1. В этом случае сумма геометрической прогрессии равна  .
. □
□ и
и  как ряд с n-ым слагаемым
как ряд с n-ым слагаемым  . Произведение ряда (1) на число l - это ряд
. Произведение ряда (1) на число l - это ряд  .
. .
.
 , и поэтому
, и поэтому  , т.е. 1 - сумма ряда (1).
, т.е. 1 - сумма ряда (1). . Для этого разложим n-ое слагаемое следующим образом:
. Для этого разложим n-ое слагаемое следующим образом:

 -- ряд с неотрицательными слагаемыми, то
-- ряд с неотрицательными слагаемыми, то  , частичные суммы ряда образуют возрастающую последовательность. Если она, к тому же еще и ограничена, то существование предела
, частичные суммы ряда образуют возрастающую последовательность. Если она, к тому же еще и ограничена, то существование предела  , т.е. сходимость ряда
, т.е. сходимость ряда  для любого натурального n начиная с некоторого номера. Если ряд
для любого натурального n начиная с некоторого номера. Если ряд  сходится, то и ряд
сходится, то и ряд  сходится. Если же ряд
сходится. Если же ряд  расходится, то ряд
расходится, то ряд  выполняется для всех
выполняется для всех  Обозначим через
Обозначим через  обозначим частичные суммы ряда
обозначим частичные суммы ряда  . Тогда
. Тогда  . Сходимость ряда
. Сходимость ряда  , что в свою очередь дает ограниченность последовательности
, что в свою очередь дает ограниченность последовательности  . По лемме получаем сходимость ряда
. По лемме получаем сходимость ряда  для любого натурального n, начиная с некоторого номера, и существует отличный от 0 предел отношения
для любого натурального n, начиная с некоторого номера, и существует отличный от 0 предел отношения  . Тогда ряды
. Тогда ряды  и
и  ведут себя одинаково в смысле сходимости (либо оба сходятся, либо оба расходятся).
ведут себя одинаково в смысле сходимости (либо оба сходятся, либо оба расходятся). . По условию
. По условию  . Предположим, что ряд
. Предположим, что ряд  начиная с некоторого
начиная с некоторого  . Отсюда вытекает неравенство
. Отсюда вытекает неравенство  . Из сходимости ряда
. Из сходимости ряда  (см. «арифметические операции с рядами»). По теореме сравнения получаем тогда, что и ряд
(см. «арифметические операции с рядами»). По теореме сравнения получаем тогда, что и ряд  (именно в этом месте нужно учесть, что
(именно в этом месте нужно учесть, что  на
на  , а
, а  на
на  . Получаем сходимость ряда
. Получаем сходимость ряда  - монотонно убывающая, непрерывная и неотрицательная функция при
- монотонно убывающая, непрерывная и неотрицательная функция при  . Положим
. Положим  для натуральных n. Тогда ряд
для натуральных n. Тогда ряд  ведут себя одинаково в смысле сходимости. При этом имеет место следующая оценка остатка ряда
ведут себя одинаково в смысле сходимости. При этом имеет место следующая оценка остатка ряда 
 (*). Если
(*). Если  ряд
ряд  сходится по теореме сравнения. Отсюда следует, что интеграл
сходится по теореме сравнения. Отсюда следует, что интеграл 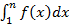 имеет предел при
имеет предел при  . Это доказывает сходимость интеграла
. Это доказывает сходимость интеграла  . Наоборот, если последний интеграл сходится и равен
. Наоборот, если последний интеграл сходится и равен 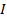 , то
, то  для любого
для любого  . Отсюда и из неравенств (*) следует ограниченность частичных сумм ряда. По лемме 1 из параграфа «теорема сравнения» вытекает сходимость ряда
. Отсюда и из неравенств (*) следует ограниченность частичных сумм ряда. По лемме 1 из параграфа «теорема сравнения» вытекает сходимость ряда 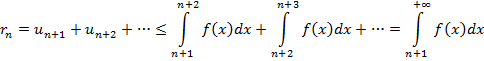
 сходится тогда и только тогда, когда
сходится тогда и только тогда, когда  . В частности, гармонический ряд расходится.
. В частности, гармонический ряд расходится. . Если
. Если 
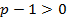 . Если
. Если  , то
, то
 неограниченно возрастающая функция. В случае
неограниченно возрастающая функция. В случае  из неравенства
из неравенства  и уже доказанной расходимости гармонического ряда
и уже доказанной расходимости гармонического ряда  вытекает расходимость ряда
вытекает расходимость ряда  (применяем теорему сравнения). □
(применяем теорему сравнения). □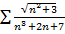 сходится, ибо
сходится, ибо  . Так как ряд
. Так как ряд  сходится (здесь
сходится (здесь  ), то по следствию теоремы сравнения получаем сходимость исходного ряда.
), то по следствию теоремы сравнения получаем сходимость исходного ряда.