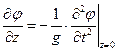|
|
Вопрос 19. Общая формулировка теории плоских свободных волн.Рассмотрим основные положения теории поверхностных гравитационных волн на свободной поверхности жидкости в водоеме конечной глубины. Жидкость считается идеальной. Интегрируя уравнения Эйлера для движения идеальной жидкости за бесконечно малый промежуток времени, можно показать, что проекции скорости Vx, Vy, Vz определяются частными производными по координатам x,y,z, т.е. удовлетворяют условию потенциальности движения жидкости. Следовательно, волновое движение является потенциальным. Физическим подтверждением этого является принцип сохранения вихрей в идеальной жидкости. Таким образом, для решения задачи о волновом движении, необходимо найти потенциал скорости волнового движения φ, представляющего собой функцию координат – φ(x,y,z,t). Примем начало координат на плоскости, совпадающей со свободной поверхностью жидкости, ось z направлена вертикально вверх. В этом случае потенциал соответствует уравнению Лапласа:
Это позволяет вычислить все характеристики волнового движения, поле скоростей и давлений. Для решения уравнения неразрывности необходимо выполнение кинематических и динамических граничных условий. Кинематические условия составляются для свободной поверхности и твердых границ водоема. zв – ординаты свободной поверхности; zв=а(f(x,y,z) уравнение свободной поверхности волн. Ее вид неизвестен и должен быть определен. На ней устанавливаются граничные условия: p=const и z= zв.
Для частиц на свободной поверхности проекция скорости частиц на ось z может быть вычислена по формуле:
Выведем граничные условия на дне и свободной поверхности жидкости. 1. Кинематические граничные условия: Учитывая, что zв – сложная функция от координат и независимой переменной t, полную производную можно записать в следующем виде:
Так как для точек свободной поверхности
На твердых границах водоема должно выполняться условие непротекания: В точках горизонтального дна
2. Динамическое граничное условие: Динамическое граничное условие на свободной поверхности соответствует постоянному давлению, равному атмосферному p0. При неустановившемся потенциальном движении давление определяется интегралом Лагранжа:
В этом уравнении
Условия (7.7), (7.8), (7.9) представляют собой математическую формулировку закона о свободных гравитационных волнах конечной амплитуды. Граничные условия 1 и 3, выполняемые на заранее неизвестной криволинейной волновой поверхности, содержат произведения и квадраты искомых величин, поэтому сформулированная задача является нелинейной и служит основанием для разработки нелинейной теории волн конечной амплитуды. Математически эта теория чрезвычайно сложна. Упростим условия на свободной поверхности, с учетом малости амплитуды волн, т.е. малости производных 1. Т.к. В результате уравнение (*) преобразуется в уравнение:
- свободную поверхность считаем плоской – первое граничное кинематическое условие. 2. Второе кинематическое граничное условие неизменно:
3. Скорости движения частиц жидкости в волнах малой амплитуды также можно считать малыми:
И из него можно найти
Дифференцируя это выражение по t, получим:
И подставив результат в (7.10), получим:
Таким образом, объединили первое динамическое и кинематическое граничные условия. Полученные граничные условия (7.11) и (7.13) являются линейными по отношению к искомой функции φ. Полученные граничные условия в сочетании с уравнением Лапласа формулируют линейную теорию волн, которую также называют теорией волн малой амплитуды. Применение этой теории позволяет пренебречь квадратами скорости в интеграле Лагранжа. Включая потенциал C(t) также в потенциал скорости φ можно вычислить избыточное давление в любой точке жидкости – т.е. узнать закон распределения давлений. Закон распределения давлений в волне запишется следующим образом:
где: p- давление на глубине z; p0 – давление на свободной поверхности. Рассмотрим плоские волны - когда образующие волновой поверхности являются прямыми линиями и картина волнового движения одинакова во всех плоскостях, совпадающих с направлением распространения волн. В плоскости XOZ уравнение Лапласа будет иметь вид:
Граничное условие на поверхности:
На дне:
Ординаты свободной поверхности:
Эти уравнения являются основными уравнениями линейной теории. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|



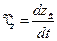

 ,
,  и с учетом того, что при потенциальном движении
и с учетом того, что при потенциальном движении  ,
, 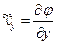 ,
,  , то уравнение (7.6) можно записать в следующем виде:
, то уравнение (7.6) можно записать в следующем виде: при
при 
 и
и  .
.

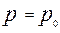 , включая p и C(t) в потенциал скорости φ с учетом того, что эти величины не зависят от координат и поэтому не влияют на поле скоростей. Тогда на основании интеграла Лагранжа с учетом
, включая p и C(t) в потенциал скорости φ с учетом того, что эти величины не зависят от координат и поэтому не влияют на поле скоростей. Тогда на основании интеграла Лагранжа с учетом  получим:
получим:
 и
и  .
. , то углы волнового склона αв малы, следовательно
, то углы волнового склона αв малы, следовательно 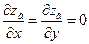
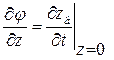
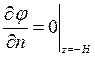
 - малы, а их произведения и квадраты еще меньше (второй порядок малости), поэтому уравнение (7.9) – третье динамическое условие на свободной поверхности будет иметь вид:
- малы, а их произведения и квадраты еще меньше (второй порядок малости), поэтому уравнение (7.9) – третье динамическое условие на свободной поверхности будет иметь вид: