
|
|
РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ (СНС),СОСТОЯЩИХ ИЗ СЖАТО-РАСТЯНУТЫХ СТЕРЖНЕЙ Под статически неопределимыми будем понимать конструкции, внутренние усилия в элементах которых, нельзя определить при помощи только уравнений статики (уравнений равновесия). СНС характеризуются наличием лишних связей в виде дополнительных закреплений, стержней и других элементов. Связи называются лишними, поскольку не являются необходимыми для обеспечения равновесия тела, а обусловлены требованиями прочности, надежности и т.д. Преимущества СНС над статически определимыми системами (СОС): 1. При одинаковых габаритах и нагрузках СНС на 10-30% легче. 2. СНС более «живучи». Недостатки СНС: 1. При неточном изготовлении, осадке опор, изменении температуры в СНС возникают дополнительные напряжения. 2. Расчет СНС значительно сложнее, чем СОС. Число лишних связей определяет степень статической неопределимости (ССН) системы ССН = п - у. Здесь: п - число независимых неизвестных реакций и внутренних усилий; у - число независимых уравнений статики для рассматриваемых систем. Для СОС п = у и ССН = 0. Для решения СНС необходимо записать дополнительные уравнения, полученные на основе рассмотрения деформации системы, которые называются уравнениями совместности (неразрывности) деформаций. Число этих уравнений должно быть равно ССН. Решение СНС выполняют в 5 этапов: 1. Анализ системы. Строится расчетная схема – система освобождается от связей (опоры заменяются реакциями), используется метод сечений (вводятся внутренние усилия). Определяется ССН. 2. Статическая сторона задачи. Для расчетной схемы записываются уравнения равновесия, включающие искомые неизвестные усилия либо реакции. 3. Геометрическая сторона задачи. Строится план перемещений – изображается, внакладку, недеформированная и деформированная система. Из геометрических соображений устанавливается связь между перемещениями отдельных элементов (стержней) конструкции. Соотношения, связывающие между собой перемещения различных стержней либо их участков, и являются уравнениями совместности деформаций. Число их равно ССН. 4.Физическая сторона задачи. Перемещения в уравнениях совместности деформаций записываются через усилия с использованием закона Гука либо других зависимостей. 5. Синтез. Решаем совместно полученную систему уравнений (уравнения равновесия + уравнения неразрывности деформаций) относительно неизвестных усилий либо реакций.
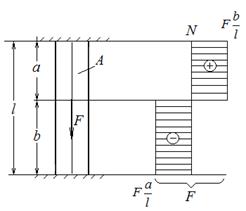
Пример 1. Для стержня постоянной жесткости ЕА, закрепленного по торцам и нагруженного в сечении, расположенном на расстоянии а от верхнего торца, силой F, определить внутренние усилия и построить эпюру N. Собственный вес стержня не учитывать (рис.1.12).
Рис.1.12 1. Анализ. Освобождаем стержень от связей (вводим неизвестные реакции опор: RA, RB) и применяем метод сечений (вводим неизвестные внутренние усилия N1, N2) (см. рис.1.13, а). Общее число неизвестных: 4 (Ra, Rb, N1, N2).
Из условий равновесия нижней и верхней частей (рис.1.13, а) получаем Ra=N1, Rb=N2. Таким образом число независимых неизвестных п=2. Принимаем в качестве неизвестных реакции опор Ra и Rb (см. рис.1.13, б), при этом имеем одно уравнение статики – у = 1 ( Определяем степень статической неопределимости ССН = п – у = 2 – 1=1. Рис.1.13 2. Статическая сторона задачи (уравнения равновесия). Для расчетной схемы (рис.1.13, б) записываем одно уравнение равновесия
3. Геометрическая сторона задачи (план перемещений). Очевидно, что длина стержня, состоящего из двух участков, при деформации, обусловленной нагружением, не изменилась, т.е. Dl=0. (*) С другой стороны, полное удлинение стержня будет определяться как сумма удлинения его участков
где: Dа и Db – удлинения верхнего и нижнего участка стержня, соответственно. Здесь необходимо отметить следующее. Из физических соображений очевидно, что верхний участок стержня будет растягиваться, а нижний сжиматься. Однако, согласно расчетной схеме (рис.1.13, б), на которой обе реакции растягивают стержень, и первый и второй участки должны растягиваться. Поэтому, для того, чтобы план перемещений стержня не противоречил расчетной схеме, будем считать, что оба участка растягиваются, и тогда на основе соотношений (*) и (**) получим
Это соотношение по своему физическому смыслу является уравнением совместности деформаций, которое записано через перемещения. 4. Физическая сторона задачи (закон Гука). Согласно закону Гука, удлинение участка «i» призматического стержня при Ni = const определяется по формуле
В соответствие с этой формулой, учитывая, что Ra=N1, Rb=N2, удлинения верхнего и нижнего участков будут равны
Подставляя выражения (1.15) в (1.14) получим уравнение неразрывности деформаций, записанное через реакции
которое, после преобразований, принимает вид
5. Синтез. Решаем совместно систему уравнений равновесия и неразрывности деформаций относительно неизвестных реакций
По полученным значениям N1 и N2 строим для стержня эпюру N.
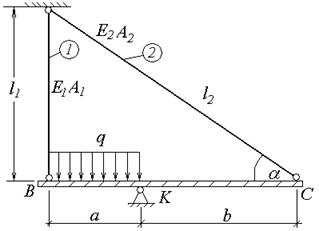
Пример 2. Для заданной системы (рис.1.14), состоящей из двух упругих стержней 1 и 2, а также абсолютно жесткого бруса ВКС, определить усилия в стержнях N1 и N2, если материал стержней сталь Ст3, l1 = 3 м, a = 2 м, b = 3 м, 2A1 = A2 = 20 см2, q = 40 кН/м. Собственный вес стержней и бруса не учитываем.
Рис.1.14 Предварительно определим недостающие параметры геометрии, а также тригонометрические функции угла a
1. Анализ.Заменяя связи реакциями и используя метод сечений строим расчетную схему стержневой системы (рис.1.15). Напомним, что, если стержень включен в конструкцию через шарниры и не подвержен действию внешних поперечных сил, в нем возникают только нормальные усилия Ni, которые по длине стержня не изменяются. Реакции, возникающие в опорах таких стержней, направлены вдоль стержня и равны, соответственно, Силовая расчетная схема
Рис.1.15 Таким образом независимых неизвестных – п = 4 (N1, N2, RK, HК). Система плоская общего вида – у = 3, откуда ССН = 4 – 3 = 1.
2. Статическая сторона задачи. Запишем для расчетной схемы уравнения равновесия, разложив, предварительно, усилие N2, на горизонтальную и вертикальную составляющие,
Уравнение моментов целесообразно записать относительно точки «К», поскольку в этом случае оно будет включать в себя минимум неизвестных величин
Здесь отметим следующее. Мы записали три уравнения равновесия, которые включают в себя все 4 неизвестных (две реакции и два усилия). Поскольку реакции, которые возникают от неподвижного шарнира, нас не интересуют, из трех уравнений равновесия имеет смысл рассматривать только одно, включающее две искомые неизвестные (N1, N2). Перепишем это уравнение, учитывая соотношения
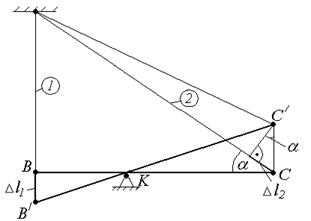
Выполнив вычисления, получим «разрешающее» уравнение статики 2N1 – 1,545N2 = 80. (1.17) 3. Геометрическая сторона задачи. Построение плана перемещений (рис.1.16) начинаем с выявления особенностей движения под нагрузкой абсолютно жесткого бруса ВКС, который в данном случае будет поворачиваться относительно точки «К». При этом, в силу гипотезы о малости деформаций, при определении перемещений точек фиксации стержней к жесткому брусу, а также их удлинений или укорочений, отрезки дуг заменяем отрезками прямых перпендикулярных к исходному либо к новому положению бруса и стержней. Углы искажений системы при деформации считаем пренебрежимо малыми. План перемещений
Рис.1.16 Построив план перемещений, выявляем связь между Dl1 и Dl2. Из подобия треугольников DКВ/В и D КС/С устанавливаем
Последнее выражение, которое перепишем в виде
представляет собой уравнение неразрывности деформаций, записанное через перемещения. 4. Физическая сторона задачи. Согласно закону Гука, удлинение (укорочение) «i» призматического стержня при Ni = const В рассматриваемом случае имеем
Знак «–» во втором выражении обусловлен различным знаком усилий в стержне 2 на расчетной схеме (стержень растягивается) и знаком его перемещений на плане перемещений (стержень сжимается). Необходимо следить за соответствием силовой схемы плану перемещений. Несоответствие устраняется на этапе рассмотрения физической стороны задачи путем изменения знака усилия. Подставляя (1.19) в (1.18) получим уравнение неразрывности деформаций, записанное через неизвестные усилия в стержнях
Подставив исходные данные и выполнив вычисления, получим «разрешающее» уравнение неразрывности деформаций в усилиях 4,64N1 + 2,97N2 = 0. (1.20)
5. Синтез. Решаем систему двух уравнений (1.17) и (1.20)
В результате получим: N1 = 18,0 кН, N2 = –28,5 кН. Знак «–» перед значением N2 указывает на то, что стержень 2 сжат. Соответствующие напряжения, вычисленные по формуле
будут равны s1 = 180 МПа, s2 = –143 МПа. Проведем несложный анализ рассмотренной статически неопределимой стержневой систем: увеличим вдвое площадь сечения стержня 1 и уменьшим вдвое площадь стержня 2, т.е. примем A1 = 2A2 = 20 см2. Очевидно, что уравнения равновесия при этом не изменятся. Уравнение неразрывности деформаций после подстановки исходных данных примет вид 2,32N1 + 5,83N2 = 0. (1.21) Решая систему двух уравнений (1.17) и (1.21), получим: N1 = 30,7 кН, N2 = –12,2 кН. Как видно из сравнения этих результатов с данными предыдущего расчета, увеличение жесткости стержня привело к увеличению в нем усилия. Этот факт характерен для всех статически неопределимых систем: стержни большей жесткости в таких системах принимают на себя большую часть нагрузки. В статически определимых системах усилия в стержнях зависят только от схемы нагружения и величины нагрузки. Заметим, что перераспределение нагрузки во втором случае способствовало снижению напряжений, которые оказались равными: s1 = 150 МПа, s2 = –122 МПа. Также уменьшилась величина суммарной реакции шарнирной опоры (R), вычисленная по формуле
В первом случае значение R составило R = 81,5 кН, во втором – R = 56,6 кН.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

 ).
). . (1.13)
. (1.13) , (**)
, (**) (1.14)
(1.14) .
.
 (1.15)
(1.15) ,
, . (1.16)
. (1.16)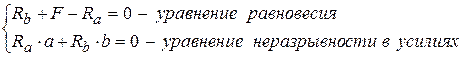
 ,
,  ;
;  , откуда
, откуда
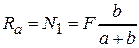
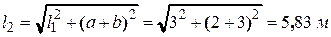 ;
; ;
;  .
. (верхняя часть расчетной схемы).
(верхняя часть расчетной схемы).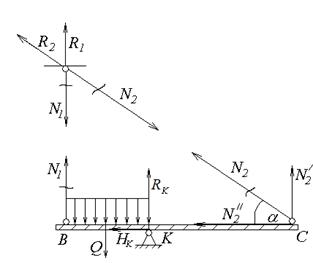
 ;
;  .
. .
. ;
;  и подставляя исходные данные задачи,
и подставляя исходные данные задачи,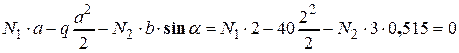
 , но
, но  , а
, а  , тогда
, тогда  .
. , (1.18)
, (1.18) .
. ;
;  . (1.19)
. (1.19) .
.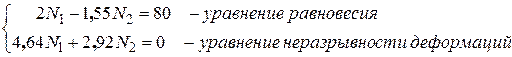
 ,
, .
.