
|
|
Нормальные алгорифмы МарковаПусть А – произвольное непустое конечное множество, называемое алфавитом, и Определение. Нормальным алгорифмом Маркова (или просто алгорифмом) в алфавите А называется конечный линейно упорядоченный список A формул подстановок слов следующих двух типов: (i) Область применения алгоритма A: 1) если левая часть u хотя бы одной формулы из A является подсловом слова w, то выбираем первую такую формулу j в списке A и заменяем первое вхождение слова u в слово w на слово v, стоящее в правой части формулы j, и ставим точку перед полученным словом 2) если же никакая левая часть формул из A не является подсловом слова w, то слово не поддается алгорифму A; Будем писать A(w)= (1) (2) алгорифм Aпросто переводит wi в wi+1 для всех (3) wn-1 |-× wn. Алгорифм A в алфавите Определение. Частичная словарная функция Понятие нормально вычислимой словарной функции удовлетворяет всем свойствам вычислимых функций, т.е. является адекватной моделью вычислений. Рекурсивные функции Пусть 0-функция, функция следования, n–местная функция проекции на m–ую координату и определяются по формулам:
для любых значений Функции На множестве F всех частичных функций нескольких числовых переменных рассмотрим следующих два оператора:
- оператор суперпозиции S ставит в соответствие каждой функции m переменных fÎF и m функциям n переменных
- оператор примитивной рекурсии R ставит в соответствие каждой функции п+2 переменных fÎF и функции n переменных gÎF функцию n+1переменных
В частности, при п = 0 схема примитивной рекурсии имеет следующий вид:
где а — постоянная одноместная функция, равная числу а. Определение. Функция fÎF называется примитивно рекурсивной (сокращенно ПРФ), если существует последовательность функций Примеры. 1. Функция сложения х+у примитивно рекурсивна в силу схемы примитивной рекурсии:
2. Функция умножения
Определение.n-арное отношение
где Примеры. Отношения равенства х = у и делимости х|у примитивно рекурсивны, т.к. функции Теорема 1. Если отношения
также примитивно рекурсивны. Теорема 2. Если отношение
Примеры. 1. Так как 2. Так как 3. Множество всех простых чисел совпадает с примитивно рекурсивным унарным отношением
На множестве F всех частичных функций нескольких числовых переменных рассмотрим еще один оператор m, который называется оператором ограниченной минимизации: каждой функции m переменных gÎF оператор m ставит в соответствие функцию m переменных f=m(g), определяемую равенством:
где правая часть равенства обозначает наименьшее решение уравнения Определение. Функция fÎF называется частично рекурсивной (сокращенно ЧРФ), если существует последовательность функций При этом частично рекурсивная функция называется рекурсивной (сокращенно РФ), если она всюду определена, и общерекурсивной, если в определяющей ее последовательности Множества всех рекурсивных, общерекурсивных, частично рекурсивных и примитивно рекурсивных функций из множества F обозначим соответственно FРФ, FЧРФ, FОРФ иFПРФ . Из определений следуют включения множеств: FПРФÌ FОРФ Ì FРФ ÌFЧРФ . Известно, что FОРФ = FРФ, но все остальные включения являются собственными, т.е. FПРФ ¹ FОРФ , FРФ ¹FЧРФ .
Определение.Подмножество A множества Определение.Подмножество A множества Конечные пересечения и конечные объединения рекурсивно перечислимых множеств являются рекурсивно перечислимыми множествами, а дополнения рекурсивно перечислимых множеств в общем случае не будут рекурсивно перечислимыми. Теорема об универсальной функции. Пусть F1 - множество всех частично рекурсивных функций f из N в N. Тогда найдется такая вычислимая функция G изN´Nв N, что для любой функции При этом уравнение Следствие. Существует рекурсивно перечислимое нерекурсивное множество. Понятия рекурсивной функции и частично рекурсивной функции, а также рекурсивного множества и рекурсивно перечислимого множества естественно переносятся на словарные функции и языки над любым конечным алфавитом
для непустого слова Такая биекция l называется лексикографической функцией для алфавита A. Лексикографическая функция l естественно продолжается на множество всех частичных словарных функций
для значений Определение. Частичная словарная функция Определение. Язык Машины Тьюринга Пост и Тьюринг исходили из того, что все действия, которые может производить любой алгоритм, можно разложить на некоторые канонические элементарные шаги, выполняемые подходяще устроенными вычислительными машинами. Такие машины строго математически определяются следующим образом. Определение.Машина Тьюринга Т - система, работающая в дискретные моменты времени t=0,1,2,... и состоящая из следующих частей: 1. Конечная лента, разбитая на конечное число ячеек, - внешня память машины. В каждый момент времени t в ячейках записаны буквы из алфавита Лента считается направленной и ее ячейки просматриваются слева направо. Таким образом, если в какой-то момент времени лента имеет r ячеек, то состояние ленты полностью описывается словом 2. Управляющая головка - устройство, которое может перемещаться вдоль ленты так, что в каждый рассматриваемый момент времени t оно находится напротив определенной ячейки и имеет некоторое состояние qj из конечного множества внутренних состояний машины В процессе работы машины управляющая головка: (1) может смещаться для просмотра соседних ячеек и (2) менять свои состояния путем замены записанных в ней букв алфавита Q на его другие буквы. 3. Список команд или программа P, представляющая собой последовательность выражений T(i,j)(где - - - Выражения T(i,j)называются командами. При этом предполагается, что команды не могут начинаться со слов q0aj, содержащих символ заключительного состояния q0, и что символы L,R не принадлежат множеству Машина Тьюринга Т - упорядоченная пятерка объектов Т=(A,Q,P,q0,q1). Работа машины Т происходит под действием команд из множества P и заключается в изменении ее конфигураций, описывающих состояния ленты и управляющей головки, а также положение управляющей головки. Если лента находится в состоянии, которое описывается словом Описывающие конфигурации K машинные слова являются словами над алфавитом К называется начальной конфигурацией, если описывающее ее машинное слово содержит символ начального состояния q1,и заключительной конфигурацией, если ее машинное слово содержит символ заключительного состояния q0. Изменение конфигураций К0,К1,К2,… машины Т под действием команд из множества P происходит в дискретные моменты времени t = 0,1,2,... и описывается преобразованием соответствующих машинных слов M0,M1,M2,…по следующему правилу. За один шаг работы машины Т ее машинное слово Символически такое одношаговое преобразование машинных слов обозначается Если существует такая последовательность преобразований машинных слов Если при этом во всех преобразованиях Для машинного слова М обозначим Слово a алфавита В этом случае будем говорить, что машина Т применима к слову a, и результат переработки машиной Т такого слова a будем обозначать Если же машина Т слово Пример. Пусть машина Тьюринга Sимеет внешний алфавит q10 → Rq2, q20 → q01, q11 → Rq1, q21 → Rq2. Тогда редуцированный алфавит имеет вид:
Машина S к любому слову над алфавитом Таким образом, машина Тьюринга Т определяет частичную функцию f из Определение. Частичная словарная функция f из Теорема. Частичная словарная функция в том и только том случае будет вычислимой по Тьюрингу, если она является частично рекурсивной функцией. Следствие. Язык Сложность вычислений В качестве модели алгоритма рассматривается машина Тьюринга T, вычисляющая числовую функцию
Временной сложностью машины T называется функция Ленточной сложностью машины T называется функция
Если внешний алфавит A машины T состоит из m символов, множество внутренних состояний Q состоит из n элементов и значение
Теорема Блюма об ускорении. Для любой рекурсивной функции Следовательно, в общем случае невозможно определить сложность наилучшего или быстрейшего алгоритма для вычисления функции Сложность алгоритмов В качестве модели алгоритма рассматривается машина Тьюринга T, вычисляющая словарную функцию Входное слово В общем случае машина Тьюринга T допускает рекурсивно-перечислимый язык Язык 1) если 2) если Если язык L рассматривается как кодировка проблемы P, то проблема P называется разрешимой, если она является рекурсивным языком, и неразрешимой в противном случае. Машины такого типа соответствуют понятию «алгоритма» и применяются при решении распознавательных задач типа «да/нет». Примеры. 1. Является ли выполнимым булев многочлен? 2. Изоморфны ли данные графы? 3. Имеет ли граф независимое множество вершин мощности k? На практике часто исходная задача является оптимизационной, т.е. предполагающей выбор оптимального решения из множества допустимых решений. Такие задачи не проще распознавательных, т.к. последние являются частным случаем оптимизационных задач. Для исследования сложности распознавательных задач далее рассматриваются машины Тьюринга T с рекурсивными языками Говорят, что машина Тьюринга T имеет временную сложность Определение. Говорят, что язык В частности, распознавательная задача принадлежит классу P, если ее язык принадлежит классу P, т.е. эта задача решается с помощью полиномиального алгоритма - некоторой детерминированной машины Тьюринга T с полиномиальной временной сложностью Пример. Задача существования для графа остова с весом не более числа k принадлежит классу P. Определение. Язык В частности, распознавательная задача принадлежит классу NP, если ее язык принадлежит классу NP, т.е. эта задача решается с помощью полиномиального недетерминированного алгоритма - некоторой недетерминированной машины Тьюринга T с полиномиальной временной сложностью Пример. Задача выполнимости булева многочлена принадлежит классу NP. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 - два символа, не входящие в алфавит А. Множество A* является множеством DA возможных исходных данных нормального алгорифма Маркова A.
- два символа, не входящие в алфавит А. Множество A* является множеством DA возможных исходных данных нормального алгорифма Маркова A.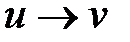 , (ii)
, (ii) 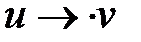 , где
, где  .
. , если формула j содержит точку, т.е. является формулой типа (ii) . Если при этом j -типа (i), то пишем w |-
, если формула j содержит точку, т.е. является формулой типа (ii) . Если при этом j -типа (i), то пишем w |-  , что
, что ,
, и
и называется алгорифмом над A.
называется алгорифмом над A.  над алфавитом называется нормально вычислимой, если существует такой алгорифм A над алфавитом
над алфавитом называется нормально вычислимой, если существует такой алгорифм A над алфавитом  , что A(
, что A( 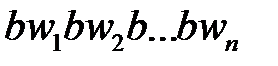 )=w тогда и только тогда, когда значение функции
)=w тогда и только тогда, когда значение функции  определено и выполняется равенство
определено и выполняется равенство  .
. – множество неотрицательных целых чисел и F – множество всех частичных функций нескольких числовых переменных из
– множество неотрицательных целых чисел и F – множество всех частичных функций нескольких числовых переменных из 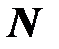 со значениями в
со значениями в  .
. и
и 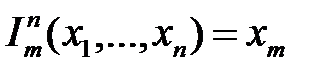

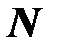 .
. ,
,  ,
, 
 называются также простейшими примитивно рекурсивными функциями.
называются также простейшими примитивно рекурсивными функциями. ÎF функцию n переменных
ÎF функцию n переменных  , определяемую равенством:
, определяемую равенством: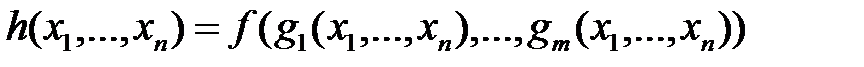 ;
;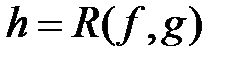 , удовлетворяющую следующей схеме примитивной рекурсии:
, удовлетворяющую следующей схеме примитивной рекурсии:  ,
,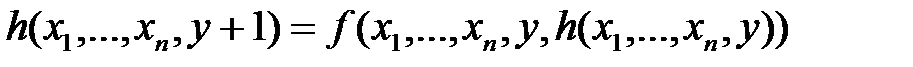 .
. ,
, ,
, ÎF, в которой
ÎF, в которой  и всякая функция
и всякая функция  является простейшей ПРФ или получается из предыдущих функций с помощью оператора суперпозиции S или оператора примитивной рекурсии R.
является простейшей ПРФ или получается из предыдущих функций с помощью оператора суперпозиции S или оператора примитивной рекурсии R.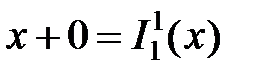 ,
,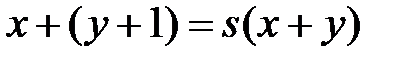 .
. примитивно рекурсивна в силу схемы примитивной рекурсии:
примитивно рекурсивна в силу схемы примитивной рекурсии: ,
, .
. называется примитивно рекурсивным (сокращенно ПРО), если примитивно рекурсивна его характеристическая функция
называется примитивно рекурсивным (сокращенно ПРО), если примитивно рекурсивна его характеристическая функция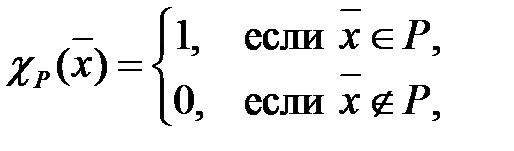
 - произвольный элемент множества
- произвольный элемент множества  .
. и
и  примитивно рекурсивны.
примитивно рекурсивны.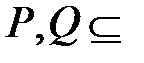
 и
и 
 примитивно рекурсивны, то отношения
примитивно рекурсивны, то отношения ,
,  ,
, 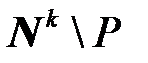 ,
, 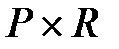

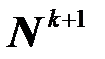 примитивно рекурсивно, то примитивно рекурсивными являются также отношения
примитивно рекурсивно, то примитивно рекурсивными являются также отношения ,
,  .
. , то отношение
, то отношение  примитивно рекурсивно.
примитивно рекурсивно. , то отношение
, то отношение  примитивно рекурсивно.
примитивно рекурсивно. .
. ,
, относительно y.
относительно y. называется рекурсивным (или разрешимым), если его характеристическая функция
называется рекурсивным (или разрешимым), если его характеристическая функция  частично рекурсивна.
частично рекурсивна. называется рекурсивно перечислимым, если A является множеством значений некоторой частично рекурсивной функции.
называется рекурсивно перечислимым, если A является множеством значений некоторой частично рекурсивной функции. F1 найдется такое nÎN, что f совпадает с частично рекурсивной функцией
F1 найдется такое nÎN, что f совпадает с частично рекурсивной функцией  изNв N.
изNв N.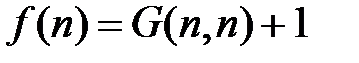 определяет вычислимую функцию из N в N определяет частично рекурсивную функцию f из N в N, которая не имеет всюду определенного рекурсивного продолжения на все множество N.
определяет вычислимую функцию из N в N определяет частично рекурсивную функцию f из N в N, которая не имеет всюду определенного рекурсивного продолжения на все множество N. с помощью биекции l множества A* на множество N,которая определяется по правилам:
с помощью биекции l множества A* на множество N,которая определяется по правилам: и
и 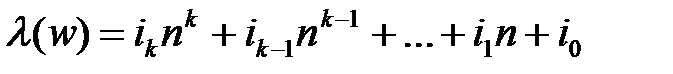
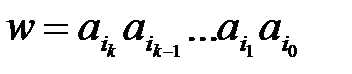 .
.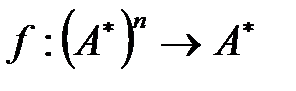 по правилу:
по правилу: есть числовая функция из
есть числовая функция из  со значениями в
со значениями в 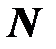 , которая определяется уравнением
, которая определяется уравнением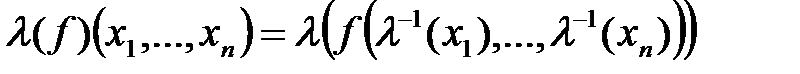

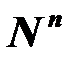 .
. называется рекурсивным (соответственно, рекурсивно перечислимым), если числовое множество
называется рекурсивным (соответственно, рекурсивно перечислимым), если числовое множество  рекурсивно (соответственно, рекурсивно перечислимо).
рекурсивно (соответственно, рекурсивно перечислимо). - внешний алфавит машины. Ячейки, в которых записан символ 0, называются пустыми. В процессе работы машины: (1) ячейки ленты могут менять свои состояния путем замены записанных в них букв алфавита A на его другие буквы и (2) к существующим ячейкам ленты может пристраиваться неограниченное число дополнительных ячеек, которые изначально считаются пустыми.
- внешний алфавит машины. Ячейки, в которых записан символ 0, называются пустыми. В процессе работы машины: (1) ячейки ленты могут менять свои состояния путем замены записанных в них букв алфавита A на его другие буквы и (2) к существующим ячейкам ленты может пристраиваться неограниченное число дополнительных ячеек, которые изначально считаются пустыми. , где
, где  – состояние первой (слева) ячейки,
– состояние первой (слева) ячейки,  – состояние второй ячейки и т.д.
– состояние второй ячейки и т.д.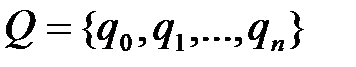 , Q∩А = Æ. Состояние q0называется заключительным и означает завершение работы машины, а состояние q1называется начальным и означает начало работы машины. Если головка в состоянии qj находится напротив ячейки в состоянии ai, то говорят, что машина просматривает эту ячейку или наблюдает ее состояние qj.
, Q∩А = Æ. Состояние q0называется заключительным и означает завершение работы машины, а состояние q1называется начальным и означает начало работы машины. Если головка в состоянии qj находится напротив ячейки в состоянии ai, то говорят, что машина просматривает эту ячейку или наблюдает ее состояние qj. ,
,  ) вида:
) вида: – означает сдвиг управляющей головки, находящейся в состоянии qi напротив ячейки с буквой aj, на одну ячейку влево с заменой состояния управляющей головки qi на состояние ql;
– означает сдвиг управляющей головки, находящейся в состоянии qi напротив ячейки с буквой aj, на одну ячейку влево с заменой состояния управляющей головки qi на состояние ql;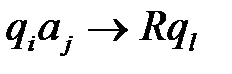 – означает сдвиг управляющей головки, находящейся в состоянии qi напротив ячейки с буквой aj, на одну ячейку вправо с заменой состояния управляющей головки qi на состояние ql;
– означает сдвиг управляющей головки, находящейся в состоянии qi напротив ячейки с буквой aj, на одну ячейку вправо с заменой состояния управляющей головки qi на состояние ql; – означает замену буквы aj в ячейке, напротив которой находится управляющая головка в состоянии qi, на букву ak с одновременной заменой состояния управляющей головки qi на состояние ql .
– означает замену буквы aj в ячейке, напротив которой находится управляющая головка в состоянии qi, на букву ak с одновременной заменой состояния управляющей головки qi на состояние ql . .
. над алфавитом A, и управляющая головка в состоянии qi просматривает на ленте j-ую ячейку с состоянием aj, то соответствующая конфигурация K машины Т описывается выражением
над алфавитом A, и управляющая головка в состоянии qi просматривает на ленте j-ую ячейку с состоянием aj, то соответствующая конфигурация K машины Т описывается выражением  , которое называется машинным словом.
, которое называется машинным словом. , правее которого в слове непременно есть символ алфавита
, правее которого в слове непременно есть символ алфавита  .
.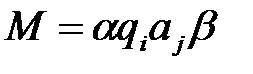 под действием команды T(i,j) преобразуется в новое машинное слово М' по формулам:
под действием команды T(i,j) преобразуется в новое машинное слово М' по формулам: , если
, если  и α=L,
и α=L, , если
, если  и
и  ,
,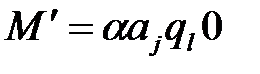 , если
, если 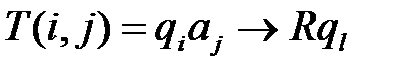 и β=L,
и β=L, , если
, если  и
и  ,
, , если
, если  .
. .
. (где
(где 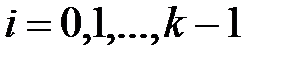 ), для которой
), для которой  и
и 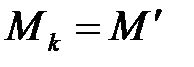 , то пишут
, то пишут  и говорят, что машинное слово М' получается из машинного слова М с помощью машины Т .
и говорят, что машинное слово М' получается из машинного слова М с помощью машины Т . (соответственно,
(соответственно,  ).
).  слово в редуцированном алфавите
слово в редуцированном алфавите  , которое получается из М вычеркиванием единственного вхождения буквы алфавита
, которое получается из М вычеркиванием единственного вхождения буквы алфавита  перерабатывается машиной Т в слово b редуцированного алфавита
перерабатывается машиной Т в слово b редуцированного алфавита 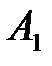 , если существует такая последовательность преобразований машинных слов
, если существует такая последовательность преобразований машинных слов  (где
(где  ,
,  - машинное слово заключительной конфигурации и
- машинное слово заключительной конфигурации и  .
. .
. , внутренний алфавит
, внутренний алфавит  и программу P:
и программу P: и слово a=11машиной S перерабатываетсяв слово b=111, так как
и слово a=11машиной S перерабатываетсяв слово b=111, так как и
и 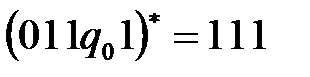 .
. в
в  , область определения которой
, область определения которой 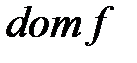 состоит из всех словалфавита
состоит из всех словалфавита  , к которым применима машина Т, и значения которой для слов
, к которым применима машина Т, и значения которой для слов  определяются по формуле:
определяются по формуле: 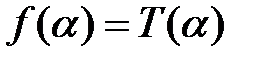 .
. в
в  , для которой при любых
, для которой при любых  условие
условие 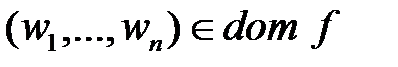 равносильно тому, что машина Т применима к слову
равносильно тому, что машина Т применима к слову  и результат
и результат  переработки машиной Т такого слова равен значению функции
переработки машиной Т такого слова равен значению функции  .
. вычислима по Тьюрингу (соответственно, язык L является множеством значений вычислимой по Тьюрингу функции).
вычислима по Тьюрингу (соответственно, язык L является множеством значений вычислимой по Тьюрингу функции). 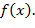
 значение которой равно числу шагов работы машины T, сделанных при вычислении значения
значение которой равно числу шагов работы машины T, сделанных при вычислении значения  если
если  определено, и
определено, и  не определено, если
не определено, если  значение которой равно числу ячеек машины T, используемых при вычислении значения
значение которой равно числу ячеек машины T, используемых при вычислении значения  не определено, если
не определено, если 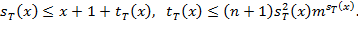
 существует такая рекурсивная функция
существует такая рекурсивная функция  что для любой машины Тьюринга T, вычисляющей функцию
что для любой машины Тьюринга T, вычисляющей функцию  , вычисляющая функцию
, вычисляющая функцию  выполняется неравенство
выполняется неравенство 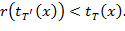

 называется допустимым машиной M, если обрабатывая это слово машина M завершает работу в заключительном состоянии, и недопустимым в противном случае. Множество всех допустимых слов образует язык
называется допустимым машиной M, если обрабатывая это слово машина M завершает работу в заключительном состоянии, и недопустимым в противном случае. Множество всех допустимых слов образует язык  , который допускается (или распознается) машиной T.
, который допускается (или распознается) машиной T.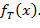
 называется рекурсивным, если рекурсивна его характеристическая функция
называется рекурсивным, если рекурсивна его характеристическая функция  , т.е.
, т.е.  Такая машина удовлетворяет условиям:
Такая машина удовлетворяет условиям: , то x – допустимое слово и, значит, при входе x машина T попадает в заключительное состояние, останавливается и выдает значение
, то x – допустимое слово и, значит, при входе x машина T попадает в заключительное состояние, останавливается и выдает значение 
 , то при входе x машина T останавливается в состоянии, не являющемся заключительным, и выдает значение
, то при входе x машина T останавливается в состоянии, не являющемся заключительным, и выдает значение 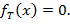

 (или «время работы
(или «время работы  для некоторой детерминированной машины Тьюринга T с временной сложностью
для некоторой детерминированной машины Тьюринга T с временной сложностью