
|
|
Локальное описание многоэлектронных атомовАТОМЫ. Термин "атом" используется для обозначения нескольких различных объектов. В структурном отношении необходимо различать атомы "физические" и химические". Химический атом — это понятие классической химии, необходимое для описания химических свойств веществ и связанное с эмпирическими химическими данными. Химический атом всегда является составной частью вещества и никогда не встречается в свободном виде. Поэтому его свойства недоступны для измерения с помощью приборов и имеют чисто конвенциональный характер. В качестве примера можно привести такие характеристики химических атомов как: - атомный вес (относительная масса), - порядковый номер в периодической таблице, - валентность, - электроотрицательность, - степень окисления, - атомные радиусы (ковалентный ионный и т.д.). Все химические атомы одного вида считаются тождественными друг другу и, следовательно, всякий химический атом имеет единственное доступное ему состояние. Другими словами, указание типа химического атома одновременно полностью определяет и все его свойства. Физический атом представляет собой микроскопическую структуру, состоящую из одного атомного ядра и электронной оболочки. Физический атом всегда существует отдельно от окружающей среды и поэтому его всегда можно поместить в прибор, произвести над ним соответствующие измерения и получить численные значения таких характеристик как: - энергия, - механические импульсы и моменты, - поляризуемость и др. Физический атом, следовательно, допускает построение стандартного механического описания через наблюдаемые, уравнения состояния и уравнения эволюции. Очевидно, что малые размеры атома требуют использования квантового варианта механики. Физический атом имеет множество доступных механических состояний и может переходить из одного такого состояния в другие за счет внешних возмущений. В отличие от химического атома, указание типа физического атома не определяет его свойства однозначно, поскольку эти свойства могут изменяться в широком диапазоне за счет внешних воздействий. Все механические модели относятся именно к физическому атому. Это, однако, не означает, что такие модели бесполезны для решения химических задач. Существуют способы, позволяющие адаптировать механические результаты, полученные для физического атома, к химической проблематике. Надо только всегда помнить о необходимости такой адаптации и не пытаться переносить результаты, полученные механическим способом, непосредственно на химические атомы.
МЕХАНИЧЕСКАЯ МОДЕЛЬ ФИЗИЧЕСКОГО АТОМА. Для сложных (составных) систем механический способ позволяет построить два типа описания, различающиеся по масштабу: глобальное и локальное. Однако наличие межчастичных взаимодействий приводит к тому, что эти два типа описаний взаимно исключают друг друга. Ввиду этой особенности, локальная механическая модель атома является приближенной и не может быть прямо проверена экспериментом. Глобальные характеристики атома можно легко найти с помощью стандартных экспериментальных процедур. Эти измерения показывают, что все атомы обладают рядом важных особенностей. 1. Энергия. При действии различных возмущающих факторов атом может переходить из одного состояния в другое, поглощая или испуская дискретные порции энергии. Это свидетельствует о наличии дискретных уровней энергии, в полном соответствии с законами квантовой механики для связанных микроструктур, в которых область пространства, доступная частицам, является ограниченной (частица в потенциальном ящике, ротатор, осциллятор и т.д.). Эти дискретные энергетические уровни называются атомными термами и обнаруживаются различными средствами: ААС (атомная абсорбционная спектроскопия), АЭС (атомная эмиссионная спектроскопия), ФЭС (фотоэлектронная спектроскопия) и т.д. 2. Механические моменты. Для атомов известен ряд эффектов, смысл которых сводится к расщеплению атомных термов под влиянием внешних магнитных (эффекты Зеемана и Пашена-Бака) и электрических (эффект Штарка) полей. Это свидетельствует о наличии дополнительных характеристик атома, которые могут иметь разные значения при постоянстве полной энергии. В качестве этих дополнительных характеристик выступают механические моменты, порождаемые циклическим (вращательным) движением электронов. Следует различать несколько разновидностей моментов. Во-первых, это полный механический момент атома J, для которого можно определить длину (модуль) и одну из проекций:
где J — квантовое число полного механического момента, а MJ — соответствующее магнитное число. С полным механически моментом связан полный магнитный момент атома m, благодаря наличию которого атом может взаимодействовать с внешними магнитными полями. Для большинства атомов направление этого вектора не совпадает с направлением вектора механического момента: m = g • g •J Это несовпадение ориентаций двух векторов обусловлено наличием двух компонент полного момента, J = L +S,которые характеризуются аналогичными парами квантовых чисел:
орбитальный момент
спиновой момент
Каждый из этих моментов характеризуется своим магнитно-механическим отношением: mL = gL •L mS = gS •S Поэтому в формуле, связывающей величины двух моментов — магнитного и механического, — имеется дополнительный множитель g, который называется "g-фактором" или "фактором Ланде" (в общем случае он представляет собой тензор 2 ранга). Все состояния атома, которые характеризуются определенными величинами квантовых чисел J, L и S, имеют одинаковую энергию и также называются "атомными термами", для обозначения которых используют специальные символы, состоящие из буквы и двух числовых индексов:
Наблюдаемые атома, которые доступны непосредственному экспериментальному измерению (энергия и моменты), могут быть также рассчитаны как собственные значения соответствующих квантово-механических операторов: AY = A • Y Решение таких уравнений дает также и явный вид глобальных волновых функций Y, которые можно пронумеровать соответствующими квантовыми числами (J, MJ, L, ML, S, MS). Детальный формализм глобального описания атома иллюстрирует задача об атоме водорода (и других одноэлектронных атомах). Для многоэлектронных атомов, наряду с внешним глобальным описанием, желательно построение и внутреннего локального описания, с учетом типов движения отдельных электронов.
Локальное описание многоэлектронных атомов В отличие от задачи глобального описания атома, в которой никаких проблем не возникает, при попытке построить соответствующее локальное описание на основе квантовой механики такие проблемы имеют место. Главная из них — неосуществимость экспериментальных измерений над отдельными составными частями атома — ядром и электронами. Следовательно, объективное построение механического описания для какой-либо отдельной частицы в составе атома оказывается невозможным. Единственная возможность обойти эту трудность заключается в отказе от "настоящего" описания строения атома и ограничение наших претензий разработкой более или менее правдоподобной структурной модели. Таких моделей, естественно, можно предложить много. Каждая из них может оказаться полезной в какой-либо области физической или химической проблематики. Для решения химических задач наиболее полезной оказывается т.н. "орбитальная модель" атома.
Орбитальная модель МЭА В основе этой модели лежит предположение о том, что каждый отдельный электрон может быть описан индивидуально. При этом остальные электроны, входящие в состав того же самого атома, рассматриваются как внешние условия, определяющие допустимые способы стационарного движения электрона. Такой подход часто обозначается как одноэлектронное приближение (ОЭП). Принятие подобного предположения позволяет приписать каждому электрону: - индивидуальное (одноэлектронное) состояние, описываемое одноэлектронной волновой функцией — атомной орбиталью (АО) или, при учете спина электрона, атомной спин-орбиталью (АСО); - набор одноэлектронных наблюдаемых, таких как энергия и механические моменты. В результате, каждому глобальному состоянию атома, заданному глобальной волновой функцией Ф и значениями глобальных наблюдаемых (Е, L, S, J) сопоставляются: 1) набор АО или АСО, 2) наборы соответствующих локальных наблюдаемых.
В нерелятивистской модели атома, когда магнитными взаимодействиями пренебрегают, атомные спин-орбитали могут быть построены в виде произведения пространственной части (yi) и спинового множителя (ci): fi = yi •ci(ci = a или b) Из общих принципов квантовой механики следует, что типы движений, доступные электронам в составе атома, не могут быть произвольными. Следовательно, АСО, описывающие состояния электронов в МЭА, должны образовывать дискретный набор, аналогичный набору Н-АСО, характерному для электрона в атоме водорода. Для нумерации АСО в составе такого набора удобно ввести квантовые числа (n, l, ml, s, ms) аналогичные квантовым числам одноэлектронного атома, но которые для каждого электрона имеют индивидуальные значения. fi (n, l, ml, s, ms) = yi (n, l, ml) •ci(s, ms) Центральная проблема орбитальной модели состоит в нахождении явного вида пространственных множителей АСО: yi = yi (xi, yi, zi) = y'i (ri, qi, ji). В квантовой механике одной частицы стационарные волновые функции находятся как собственные функции оператора Гамильтона. В орбитальной модели этот стандартный подход оказывается неприменимым из-за наличия межэлектронных взаимодействий. Поэтому явный вид орбиталей может быть установлен только путем конструирования разных вариантов и отбора. В качестве критерия отбора вариантов выступает т.н. вариационный принцип Ритца. Согласно этому принципу, в реальном атоме электроны выбирают такие способы движения, при которых обеспечивается минимум полной энергии атома. Соответственно, любые вариации этих способов приводят к повышению полной энергии. Следовательно, необходимо последовательно решить две задачи: 1) выразить полную энергию атома как функцию набора орбиталей, Е = Е (f1 , …, fi , …, fn) 2) найти минимум этой функции, d Е = 0 .
Решение первой задачи достигается решением стандартного уравнения на собственные значения для оператора Гамильтона: HФ = E • Фили E = òФ*HФ dv Для построения этого уравнения необходимо знать явный вид глобальной волновой функции атома Ф и глобального гамильтониана H. Волновую функцию атома можно построить из орбиталей в виде определителя Слэтера, что автоматически обеспечивает выполнение принципа Паули:
Такой определитель состоит из n одинаковых строк, включающих в себя список всех одноэлектронных АСО, и каждая строка соответствует определенному электрону. Волновая функция в виде определителя учитывает все возможные распределения электронов по заданному набору одноэлектронных состояний (спин-орбиталей). Полученные конструкции — глобальные волновые функции атома — подобно исходным спин-орбиталям, должны иметь вид произведения пространственной и спиновой частей: F = Y• C В тех случаях, когда однодетерминантные конструкции не распадаются в такое произведение, приходится использовать линейные комбинации двух и более определителей Слэтера (с отличающимися наборами АСО). Такие волновые функции называются "многодетерминантными". Если состояние атома описывается многодетерминантной волновой функцией, для такого атома нельзя однозначно указать электронную конфигурацию. Глобальная волновая функция, построенная через определители, обязательно является антисимметричной относительно перестановки номеров электронов. При этом возможны два случая: а)Fas = Ys• Cas (пространственный множитель симметричен) б)Fas = Yas • Cs (пространственный множитель антисимметричен) Тип симметрии пространственной и спиновой частей волновой функции имеет в ряде случаев существенное значение. От симметрии пространственной части зависит характер пространственного (орбитального) движения электронов, а, следовательно, их распределение в околоядерном пространстве и энергия их взаимного отталкивания. В результате, имеется связь между типом симметрии волновых функций и полной энергией атома. Оператор Гамильтона (без учета релятивистских магнитных взаимодействий) можно легко построить для любого атома: H = å (Ti) + å (Ui) + åå (Uij) = å (Ti + Ui) + åå (Uij) = å (hi) + åå (Uij) где Ti = (–h2/2m)Ñ2i — операторы кинетической энергии электронов, Ui = – Ze2/riN — операторы потенциальной энергии электронов в кулоновском поле ядра, Uij = e2/rij — операторы межэлектронного отталкивания. hi = (Ti + Ui) — т.н. "одноэлектронные гамильтонианы".
Располагая явным видом глобальной волновой функции и оператора Гамильтона, можно выразить полную энергию атома: E = òФ*HФ dv и проварьировать это выражение. В результате получится система уравнений, называемая уравнениями Хартри-Фока (ХФ) (hi + Uэфф)yi = ei • yi, где hi =[(–h2/2m)Ñ2i – Ze2/riN ] — одноэлектронный гамильтониан, Uэфф — эффективный потенциал, который зависит от вида всех АО, т.е. Uэфф = f(y1, y2, ..., yn). Эти уравнения требуют особого подхода к решению. Действительно, такое уравнение можно решить, если известен вид обоих операторов hiи Uэфф. Однако, сам вид эффективного потенциала зависит от тех функций, которые и требуется найти в качестве решений. В такой ситуации приходится прибегать к особому приему — итерационному методу. На первой стадии решения выбирается некоторый набор АО (например Н-АО водородоподобные атомные орбитали). С этим пробным набором составляется в явном виде оператор Uэфф и система ХФ-уравнений. Ее решение дает новый набор АО, отличающийся от исходного набора. С этим решением первой ступени составляется новое выражение Uэфф и находится следующий набор решений ХФ-уравнений, отличающийся и от исходного набора и от решения первой ступени. Затем итерационная процедура многократно повторяется до тех пор, пока наборы решений не начнут практически повторять друг друга. В конце концов получается набор АО и выражение для эффективного потенциала, которые уже невозможно улучшить таким способом. (y1, y2, ... , yn)о ¾® (Uэфф)о ¾® уравнения ХФ ¾® ¾® (y1, y2, ... , yn)1 ¾® (Uэфф)1 ¾® уравнения ХФ ¾® ¾® (y1, y2, ... , yn)2 ¾® (Uэфф)2 ¾® уравнения ХФ ¾® ¾® . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ¾® ¾® (y1, y2, ... , yn)n ¾® (Uэфф)n ¾® уравнения ХФ ¾® ¾® (y1, y2, ... , yn)* ¾® (Uэфф)* Найденные таким образом АО (y1, y2, ... , yn)* называются самосогласованными орбиталями Хартри-Фока (ХФ-АО), а соответствующие им величины ei* — орбитальными энергиями. Использование набора ХФ-АО для построения эффективного потенциала придает этому оператору простой вид функции трех переменных без индексов (Uэфф)* = Uэфф (r, q, j). Эта функция называется самосогласованным полем Хартри-Фока (ССП ХФ) для данного атома. Если записать уравнения Хартри-Фока с использованием самосогласованных выражений для АО и Uэфф, то получится следующая их форма: hi • yi* + (Uэфф)* • yi* = ei* • yi* или [h + (Uэфф)*] • y* = e* • y* или F • y* = e* • y* где составной оператор F =[h + (Uэфф)*], включающий одноэлектронный гамильтониан и эффективный потенциал, называется оператором Фока (фокиан). Другими словами, самосогласованные ХФ-АО можно рассматривать как собственные функции специального одноэлектронного оператора — оператора Фока, а орбитальные энергии ei* — собственными значениями этого оператора. Использование оператора Фока и уравнения на собственные значения F • y* = e* • y* приводит к простой физической картине: каждый электрон движется в суммарном поле атомного ядра и усредненном поле, которое создано за счет движения всех электронов, входящих в состав атома. В результате, многомерная (многоэлектронная) задача сводится к совокупности трехмерных (одноэлектронных) задач, аналогичных задаче об атоме водорода. Однако здесь имеется и принципиальное отличие. Гамильтониан для атома водорода hi =[(–h2/2m) Ñ2i – Ze2/riN ] обладает сферической симметрией, т.е. потенциальная энергия не зависит от углов q и j. Напротив, оператор Фока содержит дополнительный член, явно зависящих от этих углов. F = [hi + (Uэфф)*] = (–h2/2m) Ñ2i – Ze2/riN + Uэфф(r,q,j) По этой причине уравнение Фока не может быть решено аналитически, и его решения могут быть выражены только в табличной форме. Другими словами, может быть вычислено значение орбитали в любой конкретной точке околоядерного пространства, но для ХФ-АО не существует точных аналитических выражений типа y(r, q, j), аналогичных водородоподобным АО. Для того, чтобы преодолеть указанный недостаток ХФ-АО можно использовать специальный прием, называемый приближением центрального поля (ПЦП). В этом случае выражение для эффективного потенциала усредняют по значениям углов q и j, получая приближенное выражение, содержащее только переменную r: Uэфф (r, q, j) ¾® `Uэфф(r). Тогда оператор Фока приобретает более простой вид: `F = [hi + (`Uэфф)] = (–h2/2m) Ñ2i – Ze2/riN +`Uэфф(r) Потенциальная энергия в таком операторе зависит только от переменной r, так же как и в одноэлектронном атоме. В результате, собственные функции модифицированного оператора Фока`Fмогут быть выражены в виде произведения радиальной и угловой частей. `y = `R(r) • Y(q, j) причем угловой множитель представляет собой шаровую функцию, т.е. точно совпадает с аналогичными угловыми частями водородоподобных АО и может быть пронумерован двумя квантовыми числами l и ml. Напротив, радиальные множители ХФ-АО существенно отличаются от радиальных множителей Н-АО. Причиной является влияние межэлектронного отталкивания, выражаемое усредненным эффективным потенциалом. В приближении центрального поля движение электрона, описываемое АСО`y, происходит в потенциальной яме уже не кулоновской формы: U ¹ – Ze2/r. Эта форма модифицирована добавкой Uэфф(r), что приводит к изменению наклона стенок потенциальной ямы.
Изменение формы кулоновской потенциальной ямы приводит к тому, что каждой точке сила притяжения к ядру, действующая на электрон, оказывается меньше, чем должна быть, так как сила притяжения, порождаемая ядром, складывается с силой отталкивания, порождаемой электронным облаком. Этот эффект называется эффектом экранирования, который сказывается тем сильнее, чем больше прочих электронов находится между данным электроном и ядром. Точная форма радиальных функций`R(r) неизвестна, но может быть аппроксимирована различными приближенными выражениями. Наиболее простым вариантом являются т.н. слэтеровские АО (или орбитали Слэтера).: `R(r)n = r(n – d – 1) • exp[– r • (Z – S)/(n – d)] где n — главное квантовое число, нумерующее радиальную функцию, (n – d) = n* — т.н. "эффективное" главное квантовое число, r = r/a0 — расстояние до ядра, измеренное в атомных единицах длины, Z — зарядовое число ядра, S — константа экранирования. Поправки d (для главного квантового числа) и S (для зарядового числа ядра) вычисляются по специальным правилам Слэтера и имеют свои индивидуальные значения для каждой АО. Эффективный заряд ядра, Z* = (Z – S), рассчитанный для некоторых атомов имеет следующие величины:
Эффективное квантовое число n* соотносится с числом n следующим образом:
Слэтеровские АО отличаются одним существенным недостатком — они неправильно описывают узловую структуру радиальной части, так как из полинома Лаггера сохраняют только один главный член. Ситуацию можно значительно улучшить, если использовать линейные комбинации двух орбиталей Слэтера с разными значениями главного квантового числа. Такие выражения называются орбиталями Слэтера-Зенера или "DZ-АО" (дубль-зет). Известны и другие способы построения приближенных выражений для радиальных частей АО, которые сводятся к рядам на основе некоторых наборов базисных функций (степенных, экспоненциальных и т.д.).
Зная эффективные значения главного квантового числа и зарядового числа ядра, можно приближенно оценить орбитальные энергии (в электрон-вольтах) по формуле: e = – 13,6 (Z*)2/(n*)2 эв. Точные выражения для орбитальных энергий, характеризующих ХФ-АО, имеют вид: ei* = Hi + å Jij ± å Kij где Нi = òyi* [(–h2/2m)Ñ2i – Ze2/riN ] yi dvi — остовные интегралы Jij = òyi*yi* [ e2/rij ] yj yjdvi dvj — кулоновские интегралы Kij = òyi*yj* [ e2/rij ] yj yi dvi dvj — обменные интегралы Остовный интеграл Нi представляет собой энергию электрона, находящегося на i-ой АО (yi), при условии отсутствия остальных электронов. Кулоновский интеграл Jij представляет собой поправку, учитывающую энергию кулоновского отталкивания между двумя электронными облаками: |yi|2 = yi*•yi и |yj|2 = yj*•yj Обменный интеграл Kij представляет собой поправку особого типа, связанного с возможностью перехода электрона из одного состояния в другое: yi « yj. Необходимость такой поправки связана с изменением объема доступного пространства и узловой структуры электронного облака при переходе электрона из одного состояния в другое. Можно заметить, что обменные интегралы для пары одинаковых спин-орбиталей, отличающихся только спиновыми множителями (yia « yib), равны нулю. Зная орбитальные энергии, можно найти и полную энергию МЭА: Е = åHi + åå Jij ± åå Kij (i < j) Необходимо отметить, что полная энергия атома не равна простой сумме орбитальных энергий: Е* = åei* = åHi + åå Jij ± åå Kij поскольку в этом выражении каждая кулоновская и обменная поправка учитывается дважды. Поэтому имеет место равенство: Е = åei* – {åå Jij ± åå Kij}/2
Оболочечная модель МЭА.
Одноэлектронное приближение позволяет каждому электрону приписать свое индивидуальное состояние, характеризуемое атомной спин-орбиталью, набором одноэлектронных характеристик и даже квантовых чисел (в рамках ПЦП). Метод ССП ХФ позволяет найти точную табличную или приближенную аналитическую (слэтеровскую и др.) форму для этих АСО, причем получаемый набор АСО не связан с каким-либо конкретным электроном, а принадлежит всему атому в целом. Можно сказать, что атомное ядро за счет своего электрического заряда порождает в окружающем пространстве набор "виртуальных АО", которые могут постепенно заселяться электронами. Заселение, очевидно, должно в соответствии с некоторыми правилами. Анализ этих правил приводит к возможности выделения в атоме некоторых совокупностей электронов — электронных оболочек (или слоев) и подоболочек. Поэтому такая структурная модель МЭА называется оболочечной моделью. Классификация АО. Каждая АСО может быть охарактеризована набором квантовых чисел fi (n, l, ml, s, ms) = yi (n, l, ml) •ci(s, ms) которые аналогичны квантовым числам одноэлектронного атома (за исключением главного квантового числа, которое в МЭА не определяет однозначно энергию орбитали). В соответствии со значениями квантовых чисел n и l, орбитали многоэлектронных атомов могут классифицироваться по их узловой структуре и симметрии. Узловая структура. В радиальном направлении число узлов определяется формулой Nрадиальн. = n – l – 1 В угловых направлениях число узловых поверхностей определяется формулой: Nуглов. = l Графические (полярные) диаграммы узловой структуры аналогичны соответствующим диаграммам для атома водорода. Симметрия определяется по принадлежности АО типу симметрии (неприводимому представлению) группы симметрии шара O(3): ns-АО имеют симметрию типа S (полная симметрия, любая операция симметрии имеет характер +1), np-АО имеют симметрию типа P (антисимметричны относительно отражения в узловой плоскости, часть операций имеет характер –1), nd-АО имеют симметрию типа D (антисимметричны относительно отражения в обеих узловых плоскостях), и т.д.
Порядок заселения АО. В отношении порядка заселения АО действуют два основных правила. 1. Принцип запрета Паули: каждая АСО может быть заселена не более чем одним электроном (каждая АО — не более, чем двумя электронами с противоположно направленными спиновыми векторами). Это правило является универсальным и действующим всегда. 2. Принцип минимальной энергии. Здесь необходимо различать два типа атомов. Во-первых, атомы изолированные. Состояние, в котором находятся такие атомы, зависят от начальных условий (от начальной энергии, которая сохраняется постоянной). Во-вторых, атомы, имеющие возможность взаимодействовать с окружающей средой и обмениваться с ней энергией. Большинство реальных атомов относятся именно к этому типу. Для таких атомов можно выделить одно особое состояние, обладающее наименьшей энергией — основное, в котором атом находится наиболее часто, и множество возбужденных состояний, в которых атом бывает сравнительно редко. Принцип минимальной энергии справедлив для атомов, находящихся в основном состоянии. Практическое использование принципа минимальной энергии не так просто, поскольку речь идет о минимуме полной энергии атома, а она не складывается только из орбитальных энергий — необходимо знать все кулоновские и обменные поправки. Другими словами, каждый раз требуется решать ХФ-задачу в полном объеме. Кроме того, орбитальные энергии и поправки существенно зависят от зарядового числа ядра. Поэтому на практике часто пользуются простыми (и более приближенными) методиками, позволяющими оценить порядок заселения АО электронами. Примером такой методики могут служить известные правила Клечковского, которые увязывают порядок заселения орбитали с квантовыми числами n и l.
Порядок заселения определяется возрастанием суммы(n + l), а при равенстве этой суммы — возрастанием главного квантового числа (или уменьшением орбитального квантового числа). Правила Клечковского выполняются не всегда и допускают множество исключений (Cr, Cu, элементы VIII группы, лантаноиды).
После того, как расселение электронов завершено, атом приобретает определенную электронную конфигурацию, которую удобно описывать т.н. электронной формулой. Формула строится из подоболочек, задаваемых квантовыми числами n и l с указанием числа электронов на каждой подоболочке: (n1l1)n1(n2l2)n2(n3l3)n3.... (nklk)nk Приведем для примера электронные формулы некоторых атомов: С: 1s22s22p2; S: 1s22s22p63s23p4; Mo: 1s22s22p63s23p64s23d104p65s14d5; Можно различать подоболочки заполненные и незаполненные. Число электронов в заполненной оболочке называется ее емкостью и равно 2(2l+ 1).
По характеру заселяемой оболочки атомы можно классифицировать на типы: s-, p-, d-, f- и т.д.
Подоболочки принято объединять в слои по значению главного квантового числа n. Емкость слоя равна 2n2.
Можно легко видеть, что получающаяся картина почти точно соответствует структуре Периодической таблицы химических элементов. Это совпадение оболочечной модели атома и ПТ часто трактуется как "теоретический вывод ПТ из квантовой механики атома". В действительности ситуация обратная: оболочечная модель является всего лишь весьма грубым приближением и во многих случаях приводит к предсказаниям, противоречащим ПТ. В этих случаях оболочечную модель подгоняют по образцу ПТ, но никогда не поступают наоборот. Именно ПТ основана на надежной базе химического эксперимента, тогда как оболочечная модель служит лишь в качестве механической иллюстрации к ней. Для подтверждения приведем два высказывания выдающихся физиков: Э. Резерфорд, 1934 г. "Развитие волновой механики настолько совершенно, что периодический закон может быть выведен исходя из ее основных принципов. Любой компетентный математик был бы в состоянии построить периодическую систему, даже в том случае, если бы он никогда не слышал о периодическом законе. Ему, конечно, понадобилось бы громадное количество времени и помощь вычислителей." Ч. Коулсон, 1969 г. "Современная волновая механика не внесла достаточной ясности в детали периодической системы, но в то же время она оказалась в состоянии дать качественную, а иногда и полуколичественную, информацию по некоторым вопросам, имеющим отношение к периодической системе элементов." Заселение подоболочек. Особая проблема заключается в определении порядка заселения подоболочек, когда значения квантовых чисел n и l сохраняются постоянными, и, следовательно, правила Клечковского не действуют. Рассмотрим, например, атом азота с электронной формулой 1s22s22p3. С заполненными подоболочками 1s и 2s проблем не возникает, тогда как для незаполненной 2p-подоболочки возможно 20 различных способов заселения и, следовательно, должно существовать 20 разновидностей атома азота с указанной электронной формулой. Поскольку орбитальные энергии всех 2р-АО одинаковы, на полную энергию атома оказывают влияние малые вклады, связанные с межэлектронными силами отталкивания и еще более слабые магнитные силы, обусловленные спин-орбитальным взаимодействием. Для оценки величины этих вкладов требуется установить значения характеристик глобальных векторов орбитального и спинового моментов: | L | 2 = h2 • L(L + 1) и LZ = h • ML | S | 2 = h2 • S(S + 1) и SZ = h • MS 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
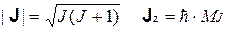

 ,
, .
.

