|
|
Примеры решения типовых задачЗадачи по математическому анализу, Задача № 1 Описать свойства наиболее распространенных в экономике и управлении функций и построить их графики. Задание А Параболическая функция Решение Для построения графика функции найдем характерные точки. Вершина параболы имеет координаты При
Задание Б .Экспоненциальная функция Решение Для построения графика функции составим таблицу.
Задание В. Тригонометрическая функция Решение Для построения графика функции составим таблицу.
Задача №2 Найти экстремумы и точки перегиба функции одной переменной Решение Согласно выполнению необходимого условия существования экстремума найдем критические (стационарные) точки данной функции. Найдем первую производную функции и приравняем ее нулю:
Решая квадратное уравнение, получаем две стационарные точки Согласно выполнению достаточного условия существования экстремума определяем характер поведения функции в стационарных точках. Найдем вторую производную функции.
Проверим стационарную точку
Так как
Проверим стационарную точку
Так как . Для нахождения точек перегиба приравняем вторую производную нулю:
откуда
Задача №3 Найти экстремумы функции двух переменных: Решение Согласно выполнению необходимого условия экстремума найдем критические (стационарные) точки данной функции. Найдем частные производные первого порядка:
Приравняем полученные производные нулю:
Решая систему уравнений, отыщем стационарные точки.
Таким образом, находим две точки Согласно выполнению достаточного условия существования экстремума определим характер поведения функции в стационарных точках. Найдем все частные производные второго порядка.
Проверим стационарную точку
Так как Проверим стационарную точку
Так как Вычислим значение этого минимума.
Задача №4 Задание а). Проинтегрировать функцию Решение Применим способ замены переменной, для подстановки положим Поэтому Задание б). Проинтегрировать рациональную функцию Разложим подынтегральную функцию на простейшие дроби:
Освобождаясь от знаменателя, получим:
Полагая последовательно Итак, тождественно Задание в). Вычислить определённый интеграл Применим способ интегрирования по частям. Обозначим
Задача 5 Дано уравнение гиперболы 16х2-9у2=144. Найти длины ее осей, координаты фокусов, эксцентриситет; составить уравнения директрис и асимптот гиперболы. Решение. Приведем уравнение гиперболы к каноническому виду и определим как параметры гиперболы, так и расстояние с от начала координат до фокуса:
откуда а=3, b=4, Действительная ось 2а=6; мнимая ось 2b=8. Уравнения директрис: Уравнения асимптот: Задача 6. Составить уравнение эллипса, симметричного относительно координатных осей, зная, что он проходит через точки М1(2;3) и М2 Решение. Учитывая симметричность эллипса относительно осей координат, его каноническое уравнение будет иметь вид
определим параметры эллипса а и b. Обозначив
получим следующую систему уравнений:
Решая ее, получим, что:
откуда а2=16, b2=12. Следовательно, искомое уравнение эллипса будет:
Задача 7. Найти вершину, фокус, ось и директрису параболы у = -2х2 +16х-29.
Решение. Преобразуем данное уравнение следующим образом:
Отсюда Обозначив х`= х-4 и у`= у-3, перейдем к новой системе координат O`x`y`, начало которой находится в точке O`(4;3), а оси O`x` и O`y` сонаправлены с осями Ох и Оу. В результате получим простейшее уравнение данной параболы
Отсюда xF = xO` = 4; т. е. F
Задача 8. Уравнение эллипса
Решение Найдем из данного уравнения параметры a, b, c, затем найдем эксцентриситет а2=4, b2=3, c2=1, Искомое уравнение будет иметь вид:
Задача 9. Данное уравнение кривой в полярных координатах
Привести его к каноническому уравнению в прямоугольных координатах. Решение. В данном уравнении
Из этой системы находим, что а=1, с=3, b2=8. Следовательно, уравнение гиперболы имеет вид:
Задача 10.Написать уравнение прямой, проходящей через две известные точки А(2;3) и В(6;-2) и вычислить длину отрезка АВ. Решение.Уравнение прямой, проходящей через две известные точки М1(x1,y1) М2(x2,y2), имеет вид:
поэтому уравнение прямой (АВ) примет вид:
Расстояние между точками М1 и М2 определяется по формуле
поэтому длина отрезка АВ:
Задача 11.Написать уравнение высоты (BN) и вычислить ее длину в треугольнике А(6;0), В(2;-3), С(-4;9). Решение:Уравнение пучка прямых, проходящих через точку М(x0,y0) имеет вид : y-y0=k(x-x0). Угловой коэффициент прямой (BN) найдем из того условия, что (ВN)^(АС). Условие перпендикулярности двух прямых, имеющих угловые коэффициенты k1, k2:
Угловой коэффициент прямой, проходящей через точки М1(x1;y1) и М2(x2;y2) - т.о.,
Для вычисления высоты BN воспользуемся формулой, определяющей расстояние d точки М0(x0;y0) до прямой, заданной уравнением Ax+By+C=0:
Нам нужно определить расстояние точки В(2;-3) до прямой, идущей через точки А(6;0) и С(-4;9). Уравнение (АС)
Задача 12.Вычислить в радианах величину внутреннего угла В в треугольнике А(4;-1), В(-4;-5), С(1;10). Решение:Для определения угла В воспользуемся формулой тангенса
В нашем случае такой прямой является (ВА) ( см.рисунок).
Задача 13. Написать уравнение (ВК) биссектрисы внутреннего угла треугольника с вершинами А(4;-1), В(-4;-5), С(1;5).
Уравнения таких биссектрис имеют вид:
Точка М(x;y), координаты которой удовлетворяют этому условию, равноудалена от двух данных прямых, так как в левой и правой части равенства записаны расстояния ее до этих прямых. В нашем случае уравнения прямых (АВ) и (ВС) имеют вид: (АВ): (BC): Уравнения двух биссектрис угла В (внутреннего и внешнего) имеют вид:
x-2y-6=2x-y+3 или y=-x-9 (1) x-2y-6=-(2x-y+3) или x-y-1=0(2) и y=x-1 (2) Из уравнений (1), (2) угловые коэффициенты этих биссектрис k=-1, k=1 Искомый угловой коэффициент должен удовлетворять неравенству: k(BA)< k(BK) <k(BC) , (см. рисунок). Так как и уравнение биссектрисы (ВК) есть x-y-1=0.
Задача 14.Составить уравнение линии, каждая точка которой вдвое дальше от прямой y+2=0, чем от точки F(-3;1). Решение:Пусть точка М(x,y) обладает указанными свойствами:
Координаты x, y точки М должны удовлетворять следующему уравнению:
После возведения в квадрат и соответствующих преобразований получим уравнение: 4x2 + 24x + 3y2 - 12y + 36=0 или 4(x2 +6x +9 - 9) + 3(y2 -4y +4 -4) - 36 = 0 ----------- ------------ 4(x + 3)2 + 3(y-2)2 - 48 + 36 = 0
Это уравнение эллипса с осями симметрии, параллельными координатным осям с центром в точке С(-3;2) и полуосями
Рис. 2 Задача 15.Составить уравнение гиперболы, симметричной относительно координатных осей, с фокусами на оси Ox, если уравнения ее асимптот Решение: Уравнение такой гиперболы имеет вид
Так как расстояние между директрисами равно
Кроме того, Для a и b получим следующую систему:
a=8, b=6 и уравнение гиперболы
Задача 16 (линейное программирование). Математическая постановка
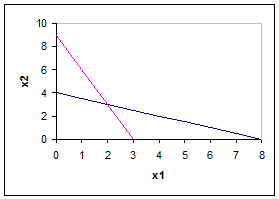
x2³0, a11x1+a12x2£b1, a21x1+a22x2£b2, F=c1x1+c2x2®max. Графическое решение задачи линейного программирования. Максимизировать функцию F=3x1+5x2 при ограничениях: 2x1+4x2£16 3x1+x2£9 a11=2 a12=4 b1=16 a21=3 a22=1 b2=9 c1=3 c2=5 Построим графики функций 2x1+4x2=16 и 3x1+x2=9, проходящие через точки (x1=0, x2=4; x1=8, x2=0) и (x1=0, x2=9; x1=3, x2=0) соответственно, а также x1=0 и x2=0 с областями определения x1³0 и x2³0 соответственно. В результате получим многоугольник ОABC, задающий область допустимых решений задачи.
Затем построим график функции 3x1+5x2=const., где const некоторое число, например, 15. Все точки (x1, x2) этой прямой придают целевой функции значение 15. Если теперь перемещать эту прямую параллельно самой себе, значение целевой функции будет меняться. Можно заметить, что максимальное значение из области допустимых решений целевая функция в данном случае принимает в точке пересечения прямых 2x1+4x2=16, 3x1+x2=9, задающих ограничения на область допустимых решений. Решением задачи является точка B с координатами x1=2, x2=3. Значение целевой функции в этой точке равно F=3×2+5×3=21. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
.

 и
и 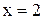
 . Корни функции
. Корни функции 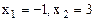

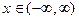 .
2.Область значений функции
.
2.Область значений функции  .
3.Функция убывает на интервале
.
3.Функция убывает на интервале  и возрастает на интервале
и возрастает на интервале  .
4.Особые точки функции: корни (-1;0) и (3;0), минимум (-1;-4); пересечение с осью y (0;-3).
5. Функция непрерывна.
.
4.Особые точки функции: корни (-1;0) и (3;0), минимум (-1;-4); пересечение с осью y (0;-3).
5. Функция непрерывна.
 ,
,  и первообразную
и первообразную 
 .
.
 .
3.Функция монотонно возрастает.
4. Особые точки функции: (0;-2) и
.
3.Функция монотонно возрастает.
4. Особые точки функции: (0;-2) и  и асимптота
и асимптота  .
5.Функция непрерывна.
6.Функция общего вида.
7.Функция непериодическая.
8. Функция имеет производные
.
5.Функция непрерывна.
6.Функция общего вида.
7.Функция непериодическая.
8. Функция имеет производные  ,
,  и первообразную
и первообразную  .
.
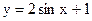




 .
2.Область значений
.
2.Область значений  .
3.Функция возрастает в интервале
.
3.Функция возрастает в интервале  и убывает в интервале
и убывает в интервале  .
.
 . минимум
. минимум  , а также корни функции, определяемые обратной тригонометрической функцией.
5.Функция непрерывна.
6.Функция нечетна относительно точки (0;1).
7.Функция периодическая, период
, а также корни функции, определяемые обратной тригонометрической функцией.
5.Функция непрерывна.
6.Функция нечетна относительно точки (0;1).
7.Функция периодическая, период  .
8. Функция имеет производные
.
8. Функция имеет производные  ,
,  и первообразную
и первообразную  .
.
 , построить график функции.
, построить график функции. ,
,  .
. .
. .
. :
: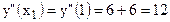
 , то в этой точке функция имеет экстремум, который является минимумом, потому что
, то в этой точке функция имеет экстремум, который является минимумом, потому что  . Вычислим значение этого минимума:
. Вычислим значение этого минимума: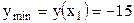
 :
: ,
, , то в этой точке функция имеет экстремум, который является максимумом, потому что
, то в этой точке функция имеет экстремум, который является максимумом, потому что  . Вычислим значение этого максимума:
. Вычислим значение этого максимума: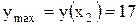
 ,
, .
.

 .
. ,
, .
.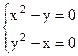



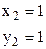
 и
и  .
. . (А)
. (А) , (В)
, (В) . (С)
. (С)


 .
.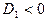 , то в точке
, то в точке  функция экстремума не имеет.
функция экстремума не имеет.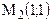


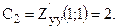
 .
. , то в точке
, то в точке  и
и  .
.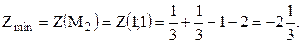

 . Дифференцируя, получим
. Дифференцируя, получим  и
и  .
. .
. .
.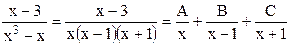 .
.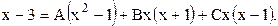
 , получим
, получим  , откуда А=3; В=-1; С=-2.
, откуда А=3; В=-1; С=-2. , поэтому
, поэтому 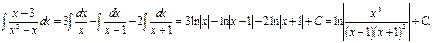
 .
. . Тогда
. Тогда  и
и  Применяя формулу интегрирования по частям, получим
Применяя формулу интегрирования по частям, получим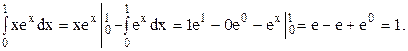
 или
или  ,
, , эксцентриситет e=
, эксцентриситет e=  .
. .
. .
. .
. , и вместо текущих координат подставим в это уравнение сначала координаты точки М1, а затем координаты точки М2. Из получившейся системы уравнений
, и вместо текущих координат подставим в это уравнение сначала координаты точки М1, а затем координаты точки М2. Из получившейся системы уравнений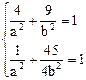
 ,
,  ,
, .
. ,
, .
.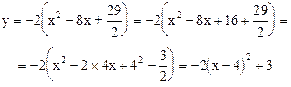
 .
. .
.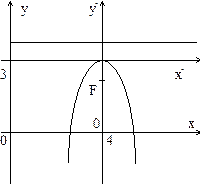
 , т. е.
, т. е.  . Итак, вершина параболы находится в точке O`(4;3); координаты фокуса
. Итак, вершина параболы находится в точке O`(4;3); координаты фокуса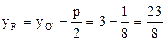
 ; уравнение оси параболы x = xO` = 4, т. е. х-4=0; уравнение директрисы
; уравнение оси параболы x = xO` = 4, т. е. х-4=0; уравнение директрисы  , т. е. 8y-25=0.
, т. е. 8y-25=0. привести в полярной системе координат к уравнению вида
привести в полярной системе координат к уравнению вида .
. и фокальный параметр эллипса
и фокальный параметр эллипса  :
: ,
,  .
.
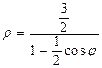 или
или  .
. .
. ,
,  . Так как эксцентриситет e>1, то данное уравнение является уравнением гиперболы, у которой b2=c2-a2. Таким образом, данные параметры могут быть записаны в виде системы двух уравнений
. Так как эксцентриситет e>1, то данное уравнение является уравнением гиперболы, у которой b2=c2-a2. Таким образом, данные параметры могут быть записаны в виде системы двух уравнений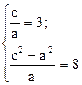
 .
. ,
, .
.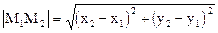
 .
. .
. ;
;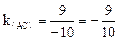
 и уравнение (BN), следовательно, имеет вид:
и уравнение (BN), следовательно, имеет вид: .
. .
.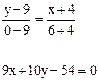
 .
.
 , где k1 – угловой коэффициент той прямой, которая поворачивается до совмещения со второй против часовой стрелки.
, где k1 – угловой коэффициент той прямой, которая поворачивается до совмещения со второй против часовой стрелки.
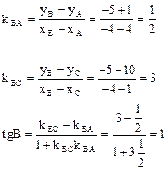
 .
.
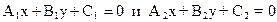
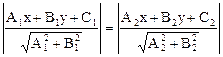
 ,
, .
. , что равносильно уравнениям:
, что равносильно уравнениям: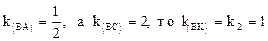
 Рис. 1
Рис. 1
 , где d - расстояние точки М до заданной прямой(рис.1).
, где d - расстояние точки М до заданной прямой(рис.1).



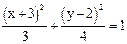
 (рис. 2).
(рис. 2).
 , а расстояние между директрисами
, а расстояние между директрисами  .
. и для его записи необходимо вычислить величины a и b. Так как уравнения асимптот гиперболы имеют вид
и для его записи необходимо вычислить величины a и b. Так как уравнения асимптот гиперболы имеют вид  , то имеем соотношение:
, то имеем соотношение: (1)
(1) , где e - эксцентриситет, то :
, где e - эксцентриситет, то : (2)
(2) поэтому условие (2) можно записать так:
поэтому условие (2) можно записать так: 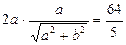
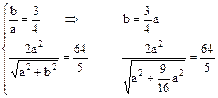
 .
. x1³0,
x1³0,