
|
|
Решение нелинейных алгебраических и трансцендентныхАЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ И МЕТОДЫ ИХ РЕШЕНИЯ
Пример формирования модели ПРИМЕР 3.1.Моделируемый объект – нелинейная цепь постоянного тока (рис. 3.1). R2 – нелинейное сопротивление.
Нелинейную вольт-амперную характеристику (ВАХ) элемента R2 аппроксимируем выражением:
Сделаем подстановку выражения (3.2) в уравнение (3.1):
(3.4)
Соотношение f(i) = 0 представляет собой математическую модель электрической цепи в форме нелинейного алгебраического уравнения относительно тока i. Решение этой модели позволит определить ток i в цепи при заданных значениях U и R1. Исследование объектов различной физической природы в установившемся режиме часто приводит к статическим моделям в форме нелинейных алгебраических уравнений. Алгебраическое уравнение К рациональнымчислам относят: · целые числа, · числа, которые можно представить в виде конечной десятичной дроби Например · числа, которые можно представить в виде периодической бесконечной десятичной дроби Например Примеры алгебраических уравнений:
В некоторых задачах моделирование приводит к трансцендентному уравнению. Трансцендентнымназываетсяуравнение, в состав которого входят трансцендентные функции: показательная, логарифмическая, тригонометрические функции, возведение в иррациональную степень. Например:
Базовые понятия Уравнение с одним неизвестным x в общем случае имеет вид: z(x) = g(x), (3.9) где z(x) и g(x) - функции, определенные на некотором числовом множестве X, называемом областью допустимых значений уравнения. Другая форма записи уравнения с одним неизвестным имеет вид: f(x) = 0, (3.10) где f(x) = z(x) – g(x) получается в результате переноса функции g(x) в левую часть уравнения (3.9). Всякое значение x*, которое при подстановке в уравнение (3.10) обращает его в числовое равенство, а функцию f(x) - в ноль, т. е. такое, что
называется корнем уравнения, или нулем функции f(x). Решить уравнение – значит, найти все его корни (решения) или доказать, что уравнение не имеет корней. Для алгебраических уравнений число корней известно заранее. Каждое алгебраическое уравнение степени n имеет в множестве комплексных чисел n корней с учетом кратности. Методы решения Аналитическое (явное) решение, т. е. решение в виде готовой формулы, выражающей неизвестное x через параметры уравнения, можно получить только для ограниченного круга уравнений, например формулы для вычисления корней квадратного (аx2+bx+c=0) и кубического (x3+px+q=0) уравнений. Решение некоторых простейших трансцендентных уравнений может быть получено в аналитической форме с использованием степенных рядов, непрерывных дробей и т. д. В большинстве случаев найти явное решение уравнения очень сложно или невозможно. Кроме того, использование аналитических формул для решения большинства уравнений не может обеспечить получение точного значения корня, поскольку коэффициенты уравнения являются приближенными величинами, определенными в результате измерений. Поэтому задача отыскания точного значения корня теряет смысл. Ставится задача – определить приближенное значение корня уравнения с заданной точностью. Приближенное решениематематических задач лежит в основе численных методов.
3.3.1. Особенности численных методов решения 3.3.1.1. Этапы численного решения нелинейного уравнения Численное решение уравнения f(x) = 0 (речь идет о действительных корнях) проводят в два этапа: 1) отделение корней, т. е. отыскание таких достаточно малых отрезков в области допустимых значений x, в которых содержится только один корень; 2) уточнение корней, т. е. вычисление корней с заданной точностью. 3.3.1.2. Отделение корней Рассмотрим несколько способов отделения корней.
y = f(x). Корень уравнения f(x) = 0 (3.12) приближенно определяется как абсцисса точки пересечения графика с осью Оx (рис. 3.2). Устанавливаются границы a и b отрезка, в пределах которого заключен только один корень x*. Способ 2 – уравнение f(x) = 0 заменяют равносильным: Строят графики функций Приближенное значение корня определяют как абсциссу точки пересечения этих графиков. Например: отделим корень уравнения
для области значений аргумента x > 0. Преобразуем уравнение (3.14) к виду:
где Строим графики функций y1 = z(x) и y2 = g(x) (рис. 3.3) и находим приближенно корень x* и отрезок Способ 3 – по таблице значений функции f(x) на заданном интервале изменения аргумента x. Например, представим таблицу значений функции
Из данных таблицы видно, что корень уравнения существует и его следует искать на отрезке [7,0; 10,0], так как значения функции на концах этого отрезка имеют разные знаки. Таблица значений функции
Способ 4 – аналитический метод отделения корней, который базируется на знании следующих свойств функции: а) если функция б)если функция Функция
 (монотонно убывающая функция). (монотонно убывающая функция).
Необходимым и достаточным условием монотонностифункции в заданном интервале является выполнение для всех внутренних точек этого интервала условия
Зная свойства функции  , можно сделать вывод о характере графика , можно сделать вывод о характере графика  , что может существенно облегчить процесс отыскания корней. Продемонстрируем это для непрерывной и монотонной на отрезке , что может существенно облегчить процесс отыскания корней. Продемонстрируем это для непрерывной и монотонной на отрезке  функции функции  , которая принимает на концах отрезка значения разных знаков, имеет во всех точках интервала первую и вторую производные , которая принимает на концах отрезка значения разных знаков, имеет во всех точках интервала первую и вторую производные  и и 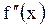 , сохраняющие постоянный знак (рис. 3.4). , сохраняющие постоянный знак (рис. 3.4).
Уточнение корней Рассмотрим два численных метода уточнения корней, применяемых для решения как алгебраических, так и трансцендентных уравнений. Эти методы относятся к разряду итерационных. Итерационный процесссостоит в последовательном шаг за шагом уточнении начального приближения x0 искомого корня. Каждый шаг такого метода называется итерацией. В результате реализации итерационного метода получают последовательность приближенных значений корня 3.3.1.3.1. Метод половинного деления (дихотомии, бисекции) Пусть дано уравнение
где функция
Требуется найти корень График функции Рассмотрим суть и этапы реализации метода половинного деления. 1) Отрезок
2) Вычисляем значение функции в точке Следует выбрать тот отрезок, на концах которого функция В данном случае (см. рис. 3.5) выбираем отрезок 3) Новый отрезок
4) Вычисляем 5) Процесс деления пополам текущего отрезка продолжаем до тех пор, пока очередной отрезок
где ε – требуемая точность расчета. За приближенное значение корня x* принимаем значение середины последнего отрезка x* = При этом погрешность вычисления корня не будет превышать Алгоритм метода половинного деления, представлен на рис. 3.6.
В блоке 2 (рис. 3.6) задается начальное значение счетчика n количества итераций (делений отрезка 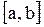 пополам). Блоки 6 – 8 реализуют выбор того из двух отрезков, на котором следует продолжать поиск корня и соответственно корректировку границы (b– при выборе левого отрезка, a– правого). пополам). Блоки 6 – 8 реализуют выбор того из двух отрезков, на котором следует продолжать поиск корня и соответственно корректировку границы (b– при выборе левого отрезка, a– правого).
Метод половинного деления – один из самых простых и надежных. Сходимость метода обеспечена для любых непрерывных функций, в том числе и для недифференцируемых. Метод устойчив к ошибкам округления. Однако скорость сходимости его меньше, чем у методов Ньютона и итерации. 3.3.1.3.2. Метод Ньютона Требуется решить уравнение Рассмотрим геометрическую интерпретацию метода Ньютона (рис. 3.7). 1) Выбираем за начальное приближение корня следует принять тот конец отрезка
Этоусловие сходимости метода Ньютона.
Основываясь на свойствах данной функции f(x) (см. рис. 3.4), делаем вывод: условие сходимости выполняется для точки  , поэтому принимаем , поэтому принимаем 
2) Вычисляем значение функции Известно, что уравнение касательной, проведенной в точке B0 с координатами (x0, f(x0)) к кривой функции f(x), имеет вид:
где x, y – текущие координаты точки, лежащей на касательной. Для точки x1 сделаем подстановку в уравнение касательной (3.24): x = x1; (3.25)
получаем:
Обе части уравнения (3.27) делим на
3) Вычисляем значение функции
4) Продолжаем последовательно проводить касательные и определять точки их пересечения с осью Оx. Тогда для текущего k-го приближения корня итерационный процесс реализуется рекуррентной формулой:
Процесс уточнения корня прекращается, когда выполнится условие близости двух последовательных приближений:
Алгоритм, реализующий метод Ньютона, представлен на рис. 3.8. Блок 4 реализует проверку условия сходимости метода и выбор значения начального приближения (блоки 5, 6). Блок 10 реализует подсчет количества итераций, 11 – вычисление текущего приближения корня через предыдущее приближение. Метод Ньютона обладает высокой скоростью сходимости, которая тем выше, чем больше крутизна графика функции Неудачно выбранное начальное приближение может привести к расходимости метода (см. рис. 3.7): представим, что за начальное приближение x0 принят левый конец отрезка a, касательная, проведенная в точке А0, пересекает ось Оx за пределами заданного отрезка [a,b]. Таким образом, получили первое приближение к корню ‹x1›, еще дальше отстоящее от искомого значения корня x*, чем нулевое приближение 3.3.1.3.3. Метод итерации Пусть требуется решить нелинейное уравнениеf(x) = 0. Преобразуем исходное уравнение одним из известных способов к виду:
где На заданном отрезке [a, b] выбираем начальное (нулевое) приближение корня x0 и подставляем его в правую часть уравнения (3.32). Получаем первое приближение корня x1:
Аналогичным образом определим второе приближение корня x2:
Продолжая этот процесс далее, получаем последовательность приближений корня x0, x1, x2, … , xn, … , определяемых соотношением:
Итерационные вычисления по формуле (3.35) продолжают до тех пор, пока для двух последовательных приближений корня xn-1 и xn не выполнится условие:
Достаточным условием сходимости метода итерации, гарантирующим, что последовательно определяемые значения x1, x2, x3, … , xn будут приближаться к искомому корню x* уравнения f(x) = 0, является условие:
причем скорость сходимости метода будет тем больше, чем меньше значение q. Рассмотрим геометрическую интерпретацию метода итерации. Исходное уравнение f(x) = 0 приводим к виду:
Строим графики функций y = x и y = Рассмотрим несколько вариантов итерационного процесса уточнения корня. Вариант 1.
Задаем начальное приближение корня  . Определяем . Определяем  . .
Через точку А0 с координатами
Вариант 3. Вариант 4.
Алгоритм, реализующий метод итерации, представлен на рис. 3.13. Решение нелинейных алгебраических и трансцендентных 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 По закону Кирхгофа
По закону Кирхгофа (3.1)
(3.1) (3.2)
(3.2) (3.3)
(3.3) или
или может содержать только алгебраические функции, в которых над переменной x производятся арифметические операции, возведение в степень с рациональным показателем и извлечение корня.
может содержать только алгебраические функции, в которых над переменной x производятся арифметические операции, возведение в степень с рациональным показателем и извлечение корня.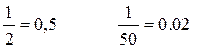
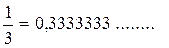
 (3.5)
(3.5) (3.6)
(3.6) (3.7)
(3.7) (3.8)
(3.8) (3.11)
(3.11) Способ 1 – по графику функции
Способ 1 – по графику функции . (3.13)
. (3.13) и
и 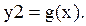
 (3.14)
(3.14)
 (3.15)
(3.15)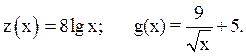
 .
. . (3.16)
. (3.16) непрерывна на отрезке
непрерывна на отрезке  и принимает на концах этого отрезка значения разных знаков, то внутри отрезка
и принимает на концах этого отрезка значения разных знаков, то внутри отрезка 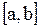 существует по крайней мере один корень уравнения
существует по крайней мере один корень уравнения  ;
; сохраняет постоянный знак внутри отрезка, то внутри этого отрезка существует корень уравнения
сохраняет постоянный знак внутри отрезка, то внутри этого отрезка существует корень уравнения  и притом единственный.
и притом единственный. называется монотонной в заданном интервале, если при любых
называется монотонной в заданном интервале, если при любых 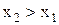 из этого интервала она удовлетворяет условию
из этого интервала она удовлетворяет условию 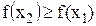 (монотонно возрастающая функция)
(монотонно возрастающая функция)  или
или 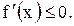

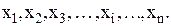 Если эти значения с увеличением n приближаются к истинному значению корня x*, то говорят, что итерационный процесс сходится.
Если эти значения с увеличением n приближаются к истинному значению корня x*, то говорят, что итерационный процесс сходится. (3.17)
(3.17) непрерывна и монотонна на отрезке
непрерывна и монотонна на отрезке  (3.18)
(3.18) уравнения (3.17) с точностью до
уравнения (3.17) с точностью до 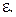
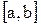 делим пополам и определяем середину отрезка:
делим пополам и определяем середину отрезка: (3.19)
(3.19) Если
Если  , то
, то  является корнем уравнения. Если
является корнем уравнения. Если  то поиск корня продолжается на одном из двух полученных отрезков –
то поиск корня продолжается на одном из двух полученных отрезков –  или
или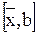 .
. , так как для него выполняется условие:
, так как для него выполняется условие:  Для того чтобы сохранить в дальнейших расчетах единое обозначение
Для того чтобы сохранить в дальнейших расчетах единое обозначение  : b =
: b =  . С точки зрения геометрической интерпретации (см. рис. 3.5) это означает, что правая граница исходного отрезка точка b переносится в точку
. С точки зрения геометрической интерпретации (см. рис. 3.5) это означает, что правая граница исходного отрезка точка b переносится в точку  снова делим пополам:
снова делим пополам:
 (3.20)
(3.20)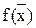 и проводим анализ двух вновь полученных отрезков –
и проводим анализ двух вновь полученных отрезков –  и
и 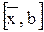 .Выбираем тот из них, для которого выполняется условие противоположности знаков функции в граничных точках.
.Выбираем тот из них, для которого выполняется условие противоположности знаков функции в граничных точках. не будет удовлетворять условию:
не будет удовлетворять условию: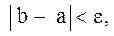 (3.21)
(3.21) , т. е.
, т. е.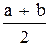 . (3.22)
. (3.22) , где n – количество произведенных делений отрезков (количество итераций).
, где n – количество произведенных делений отрезков (количество итераций).
 , причем
, причем  и
и  определены, непрерывны и сохраняют постоянные знаки на отрезке
определены, непрерывны и сохраняют постоянные знаки на отрезке 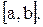
 – начальное приближение корня x*. При этом надо придерживаться следующего правила:
– начальное приближение корня x*. При этом надо придерживаться следующего правила: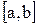 , в котором знак функции совпадает со знаком второй производной, т.е. выполняется условие:
, в котором знак функции совпадает со знаком второй производной, т.е. выполняется условие: (3.23)
(3.23)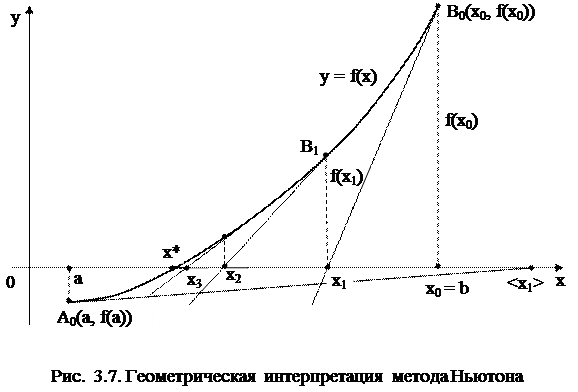
 . Проводим касательную к кривой
. Проводим касательную к кривой 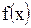 в точке
в точке  . Абсцисса точки пересечения касательной с осью Оx принимается за новое (первое) приближение корня x1.
. Абсцисса точки пересечения касательной с осью Оx принимается за новое (первое) приближение корня x1. (3.24)
(3.24) (3.26)
(3.26) . (3.27)
. (3.27) и выражаем x1:
и выражаем x1: (3.28)
(3.28) в точке x1, проводим касательную к кривой
в точке x1, проводим касательную к кривой  в точке
в точке  Абсцисса точки пересечения касательной с осью Оx представляет собой второе приближение корня x2:
Абсцисса точки пересечения касательной с осью Оx представляет собой второе приближение корня x2: (3.29)
(3.29) (3.30)
(3.30) (3.31)
(3.31)
 мало вблизи корня, то процесс уточнения корня может оказаться очень долгим.
мало вблизи корня, то процесс уточнения корня может оказаться очень долгим. .
. , (3.32)
, (3.32) - эквивалентная функция.
- эквивалентная функция. (3.33)
(3.33) (3.34)
(3.34) (3.35)
(3.35) (3.36)
(3.36) для
для  , (3.37)
, (3.37) (3.38)
(3.38) . Абсцисса точки пересечения этих графиков и будет являться корнем x* уравнения f(x) = 0.
. Абсцисса точки пересечения этих графиков и будет являться корнем x* уравнения f(x) = 0. (рис. 3.9).
(рис. 3.9).
 проводим горизонтальную линию до пересечения с прямой y = x в точке В1. Через точку В1 проводим вертикальную линию, пересекающую кривую y =
проводим горизонтальную линию до пересечения с прямой y = x в точке В1. Через точку В1 проводим вертикальную линию, пересекающую кривую y =  и ось Оx. Точка пересечения этой линии с осью Оx даст первое приближение корня x1, а точка пересечения ее с кривой y=
и ось Оx. Точка пересечения этой линии с осью Оx даст первое приближение корня x1, а точка пересечения ее с кривой y=  – точку А1 с координатами
– точку А1 с координатами  . Через точку А1 проводим горизонтальную линию до пересечения с прямой y = x (точка В2). Вертикальная линия, проведенная через точку В2, пересекая ось Оx, даст второе приближение корня x2, а также определит на кривой y =
. Через точку А1 проводим горизонтальную линию до пересечения с прямой y = x (точка В2). Вертикальная линия, проведенная через точку В2, пересекая ось Оx, даст второе приближение корня x2, а также определит на кривой y =  точку А2 с координатами
точку А2 с координатами  . Продолжая действия по той же схеме, получаем на оси Оx последовательность значений x0, x1, x2, x3, … , xn, приближающихся (сходящихся) к истинному значению корня x*. Причем все последовательные приближения x0, x1, x2, x3, … , xn находятся с одной стороны от корня x* (см. рис. 3.9). Такая сходимость называется монотонной или односторонней.
. Продолжая действия по той же схеме, получаем на оси Оx последовательность значений x0, x1, x2, x3, … , xn, приближающихся (сходящихся) к истинному значению корня x*. Причем все последовательные приближения x0, x1, x2, x3, … , xn находятся с одной стороны от корня x* (см. рис. 3.9). Такая сходимость называется монотонной или односторонней. Вариант 2.
Вариант 2. 
 (рис. 3.10). Итерационный процесс расходится.
(рис. 3.10). Итерационный процесс расходится.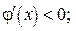
 (рис. 3.11). Итерационный процесс сходится. Процесс сходимости носит колебательный характер (двусторонняя сходимость). Последовательные приближения корня x0, x1, x2, x3, … , xn расположены по разные стороны от x*.
(рис. 3.11). Итерационный процесс сходится. Процесс сходимости носит колебательный характер (двусторонняя сходимость). Последовательные приближения корня x0, x1, x2, x3, … , xn расположены по разные стороны от x*.
 (рис. 3.12). Итерационный процесс расходится.
(рис. 3.12). Итерационный процесс расходится.
 может быть осуществлено различными способами. Выбор конкретного способа определяется целью – получить такую функцию
может быть осуществлено различными способами. Выбор конкретного способа определяется целью – получить такую функцию  , длякоторой выполняется условие сходимости
, длякоторой выполняется условие сходимости . (3.39)
. (3.39)