
|
|
Фундаментальная система решений линейного однородного уравнения
Определение. Любые Из предыдущих теорем сразу следует еще одна важная теорема. Теорема 7. Решения Доказательство. Равносильная переформулировка утверждения теоремы – решения Теорема 8. Для любого линейного однородного дифференциального уравнения (2) существует фундаментальная система его решений. Доказательство. Построим такую фундаментальную систему решений. Для этого возьмем произвольную точку По теореме 1 о существовании и единственности у каждой из этих задач имеется решение, и мы обозначим Теорема 9. Пусть Доказательство. Возьмем произвольную точку Замечание. Теоремы 8 и 9 означают, что размерность векторного пространства решений уравнения (2) равна Система линейных уравнений. Теорема Кронекера-Капелли без доказательства. Системой линейных алебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. Совместная система называется определённой, если она имеет единственное решение, и неопределённой, если имеет более одного решения. Частным решением системы называется каждое решение неопределённой системы. Общим решением называется совокупность всех частных решений системы. Система лу называется однородной, если все свободные члены равны нулю. Тривиальным называется решение, когда все неизвестные раны нулю. Теорема: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы. Теоремы: Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение. Если ранг совместной матрицы меньше числа неизвестных, то система имеет бесчисленное множество решений. Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг её основной матрицы был меньше числа неизвестных. Для того, чтобы однородная система n линейных уравнений с n неизвестными имела ненулевые решения, необходимо и лостаточно, чтобы её определитель был равен нулю. 16 Векторы, линейные операции над векторами, их свойства. {определение …} Вектор – направленный отрезок, который можно передвигать параллельно самому себе. Два вектора называются равными, если при параллельном переносе, совмещающим начала, совмещаются и концы. Модулем вектора называется длина вектора (равная корню из суммы квадратов координат). Если модуль вектора равен 1, то вектор единичный. Два вектора называются коллинеарными, если они лежат на параллельных или совпадающих прямых. Три вектора называются компланарными, если при их параллельном переносе, совмещающим начала, они оказываются лежащими в одной плоскости. Углом между двумя векторами называется угол, полученный при параллельном переносе векторов в общее начало. ω=0– векторы сонаправлены ω=p - противонаправлены ω=p/2 – перпендикулярны Суммой двух векторов является вектор идущий из начала первого вектора в конец второго, если конец первого и начало второго совмещены параллельным переносом. Суммой двух векторов называется вектор, являющийся диагональю в параллелограмме, стороны которого образованны параллельным переносом векторов в общее начало, и исходящий из точки совмещения. Разностью двух векторов является вектор идущий из конца второго вектора в конец первого, если их начала совмещены параллельным переносом. Произведением вектора на число называется вектор, коллинеарный данному, длина которого равна произведению длины данного вектора на число. Если число <0, то вектор, полученный произведением данного вектора на число, будет противонаправлен данному вектору. 1 2 3 4 – 5 l* 6 a(b 7 a( 8 (a+b) Проекция и координаты вектора {опр., св-ва} Осью называется прямая с выбранным направлением, началом и единицей длины. Проекцией точки А на прямую е называется точка А’, в которой пересекается прямая е с плоскостью, перпендикулярной е и проходящей через точку А’. Проекцией вектора AB на прямую е называется вектор A’B’, где A’ и B’ соответственно проекции точек A и B на прямую е. Числовая проекция вектора а на прямую е есть длина проекции а на прямую е или произведение длины вектора а на cos угла между вектором а и прямой е. 1) 2) 3) свойства проекций 1. прe 2. пр2 3. пре( Док-во 3-го св-ва: при a>0 имеем пре(a* при a<0: пре(a* a=0 a* Разложение вектора по ортам координатных осей
Координаты вектора – числовые проекции на координатные оси. Координаты вектора равны разностям соответствующих координат его конца и начала. Скалярное произведение двух векторов, его свойства. Условия перпендикулярности векторов. Неравенство Буняковского. Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Т.е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором. Св-ва скалярного произведения: 1.Переместительное
2. Сочетательное 3. Распределительное т.к. 4. Скалярный квадрат вектора равен квадрату его длины
5. Если два ненулевых вектора взаимо перепендикулярны, то их скалярное произведение равно нулю (т.к. косинус 900 равен нулю).
Неравенство Буняковского.
Скалярное произвкдкние векторов в коорднинатной форме Пусть заданы два вектора найдём скалярное произведение, используя таблицу скалярного произведени векторов Скалярное произведение векторов равно сумме произведений их одноимённыйх координат Векторное произведение двух векторов. Условие коллинеарносити двух векторов. Антикоммутативность векторного произведения. Векторное произведение в координатной форме. Векторным призведением вектора 1) перпендикулярен векторам 2) имеет длину, численно равную площади параллелонрамма, построенного на векторах 3) векторы
Два вектора коллинеарны, если их векторное произведение равно нулю.
Вектороное произведение в координатной форме
Смешанное произведение векторов. Условие компланарности трёх векторов. Смешанное произведение в координатной форме. Смешанным произведением векторов Св-ва смешанного произведения: 1) не меняется при циклической перестановке сомножителей, т.е. 2) не меняется при перемене мест знаков векторного и скалярного умножения 3) меняет знак при перемене мест любых двух векторов-сомножителей, т.е. 4) смешанное произведение ненулевых векторов Выражение смешанного произведения черкз коорлинаты:
Уравнение плоскости, проходящей через заданную точку и имеющую заданный нормальный вектор. Общее уравнение плоскости. Пусть плоскость Q задана в пространстве точкой M0(x0,y0,z0) и вектором Общее уравнение плоскости: Геометрическое значение коэффициентов A, B, и С в общкм уравнении плоскости Ах+By+Cz+D=0 Состоит в том что они являются проекциями на координатные оси Ox,Oy, Oz вектораб перпендикулярного этой плоскости. Положение прямой на плоскости может быть задано одним из следующих способов: · прямая l проходит через точку · прямая l проходит через точки · прямая l проходит через точку · прямая l проходит через точку
Любой вектор Пусть прямая l задана точкой
Обозначим
Переменная t, принимающая различные значения, называется параметром, а уравнение – векторно-параметрическим уравнением прямой. Если ввести систему координат
где
Эти уравнения называются параметрическими уравнениями прямой. Пусть Если
Это уравнение задает прямую, параллельную оси Oy и проходящую через точку
проходит через точку Как было отмечено ранее, направляющим вектором прямой можно выбрать вектор
Рассмотрим уравнение прямой, проходящей через две точки
или
Это уравнение называется уравнением прямой в отрезках, так как числа a и b указывают, какие отрезки отсекает прямая на осях координат. Пусть
Это уравнение прямой, проходящей через данную точку
В § 11.4 было показано, что любая прямая может быть задана этим уравнением при условии При рассмотрении векторно-параметрического уравнения прямой мы показали, как перейти к каноническому уравнению, из которого легко получить общее уравнение прямой. Аналогично, из нормального векторного уравнения так же легко перейти к общему уравнению прямой. Покажем теперь, как из общего уравнения прямой получить ее векторные уравнения. Пусть прямая задана общим уравнением Ax + By + C = 0 в прямоугольной декартовой системе координат. Тогда мы знаем, что вектор
Понятие о линейном пространстве. Единственность нулевого и противоположного элементов.
Определение. Арифметическим вектором называятся упорядоченная совокупность n чисел. Обозначается Для арифметических векторов определены линейные операции — сложение арифметических векторов и умножение вектора на число: Определение. Множество арифметических векторов, для которых определены операции сложения и умножения на число называется пространством рифметических векторовRn. Вектор противоположным вектором для вектора Для любых 1. 2. 3. 4. 5. 6. 7. 8. Примерами пространства арифметических векторов являются пространства геометрических векторов на плоскости, записанных в координатной форме Линейные подпространства в Rn, размерность подпространства, базис в подпространстве Определение. Множество L векторов из Rn , такое, что для любых Пример.Множество L арифметических векторов из Rn, у которых последние компоненты — нулевые, образует линейное подпространство в Rn:
Определение. Число k называется размерностью линейного подпространства L, еслив L существует система из k линейно независимых векторов, а любые k+1 вектора — линейно зависимы; обозначаем dimL=k. Определение. Любая линейно независимая система из k векторов k-мерного линейного подпространства L образует базис линейного подпространства L. Это означает, что если dimL=k и арифметические векторы 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 линейно независимых решений линейного однородного дифференциального уравнения
линейно независимых решений линейного однородного дифференциального уравнения  уравнения (2) образуют фундаментальную систему решений этого уравнения тогда и только тогда, когда их определитель Вронского
уравнения (2) образуют фундаментальную систему решений этого уравнения тогда и только тогда, когда их определитель Вронского  отличен от 0 хотя бы в одной точке
отличен от 0 хотя бы в одной точке  .
. на
на  . Но это утверждение сразу следует из теорем 5 и 6.
. Но это утверждение сразу следует из теорем 5 и 6. .
. - решение 1-й задачи,
- решение 1-й задачи,  - решение 2-й задачи, …,
- решение 2-й задачи, …,  - решение
- решение  для этих функций:
для этих функций:  . Следовательно, по теореме 7, функции
. Следовательно, по теореме 7, функции  этого уравнения существуют постоянные
этого уравнения существуют постоянные  такие, что
такие, что  .
. и рассмотрим систему уравнений относительно неизвестных
и рассмотрим систему уравнений относительно неизвестных  (11). Определитель этой системы
(11). Определитель этой системы  не равен 0, т.к.
не равен 0, т.к.  - фундаментальная система решений. Поэтому у нее существует (и притом единственное) решение
- фундаментальная система решений. Поэтому у нее существует (и притом единственное) решение  . По теореме 2 она является решением уравнения (2). Ввиду равенств (11) значения этой функции и ее производных до порядка
. По теореме 2 она является решением уравнения (2). Ввиду равенств (11) значения этой функции и ее производных до порядка  включительно в точке
включительно в точке 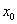 совпадают со значениями
совпадают со значениями  .
. , где чила
, где чила  ,
,  ,
,  называются коэффициентами системы, числа
называются коэффициентами системы, числа  - свободными членами. Системы лу удобно записывать в виде матрицы.
- свободными членами. Системы лу удобно записывать в виде матрицы. +
+  =
=  )=(
)=(  =
= 









 , модуль
, модуль  ;
;



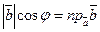
 .
.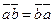 Док-во:
Док-во:
 а т.к.
а т.к.  и
и  =
=  то
то  т.к
т.к 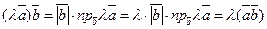


 , т.к.
, т.к.
 или
или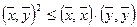
 и
и 
 :
:  получится
получится 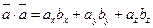 .
. на вектор
на вектор  называестя вектор
называестя вектор 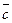 , который:
, который: и
и 


 , если заданы два вектора
, если заданы два вектора  . Смешанное произведение есть число, равное объёму параллелипипеда, построенного этих векторах, взятому с +, если эти вектора образуют правую тройку, и с -, если левую.
. Смешанное произведение есть число, равное объёму параллелипипеда, построенного этих векторах, взятому с +, если эти вектора образуют правую тройку, и с -, если левую.
 ,
,  ,
, 
 Смешанное произведение равно определителю третьего порядка, составленному из координат перемножаемых векторов.
Смешанное произведение равно определителю третьего порядка, составленному из координат перемножаемых векторов. , перпендикулярным этой плоскости. Возьмём на плоскости точку M(x,y,z) и составим вектор
, перпендикулярным этой плоскости. Возьмём на плоскости точку M(x,y,z) и составим вектор 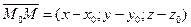 При любом расположении точки M на плоскоти Q векторы
При любом расположении точки M на плоскоти Q векторы  и
и  перендикулярны, поэтому их скалярное произведение рано нулю, т.е
перендикулярны, поэтому их скалярное произведение рано нулю, т.е 


 параллельно вектору
параллельно вектору 
 и
и 
 угол α (см. рис. 11.5.1).
угол α (см. рис. 11.5.1).
 параллельный прямой l, называется направляющим вектором этой прямой. Любой вектор
параллельный прямой l, называется направляющим вектором этой прямой. Любой вектор  перпендикулярный прямой l, называется нормальным вектором прямой. Если взять на прямой какие-либо две фиксированные точки
перпендикулярный прямой l, называется нормальным вектором прямой. Если взять на прямой какие-либо две фиксированные точки  то вектор
то вектор  в частности, будет направляющим вектором прямой
в частности, будет направляющим вектором прямой 
 (см. рис. 11.5.2). Пусть M – произвольная точка прямой.
(см. рис. 11.5.2). Пусть M – произвольная точка прямой.

 и
и  радиус-векторы точек
радиус-векторы точек  параллелен прямой, и, следовательно, вектору
параллелен прямой, и, следовательно, вектору 
 то уравнение можно записать в виде
то уравнение можно записать в виде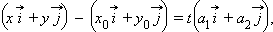
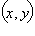 и
и  – координаты точек
– координаты точек  – координаты вектора
– координаты вектора  Отсюда следует, что
Отсюда следует, что
 и
и  тогда из уравнений следует, что
тогда из уравнений следует, что 
 и, окончательно, уравнение
и, окончательно, уравнение  которое называется каноническим уравнением прямой, с направляющим вектором
которое называется каноническим уравнением прямой, с направляющим вектором 
 то параметрическое уравнение примет вид
то параметрическое уравнение примет вид
 Каноническое уравнение прямой имеет вид
Каноническое уравнение прямой имеет вид  Аналогично, если
Аналогично, если  то прямая, задаваемая системой
то прямая, задаваемая системой
 параллельно оси Ox. Ее каноническое уравнение имеет вид
параллельно оси Ox. Ее каноническое уравнение имеет вид 
 где
где  – произвольные две точки прямой. Тогда, подставив координаты вектора
– произвольные две точки прямой. Тогда, подставив координаты вектора 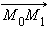 в каноническое уравнение, получим уравнение прямой, проходящей через две заданные точки:
в каноническое уравнение, получим уравнение прямой, проходящей через две заданные точки:
 а вторая лежит на оси Oy и имеет координаты
а вторая лежит на оси Oy и имеет координаты  Подставляя их в уравнение, получим
Подставляя их в уравнение, получим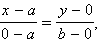

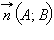 – вектор, перпендикулярный прямой, а
– вектор, перпендикулярный прямой, а  – произвольная точка этой прямой (см. рис. 11.5.3). Тогда M лежит на прямой тогда и только тогда, когда вектор
– произвольная точка этой прямой (см. рис. 11.5.3). Тогда M лежит на прямой тогда и только тогда, когда вектор  перпендикулярен вектору
перпендикулярен вектору 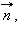 а для этого необходимо и достаточно, чтобы скалярное произведение векторов
а для этого необходимо и достаточно, чтобы скалярное произведение векторов  и
и  Введя радиус-векторы
Введя радиус-векторы 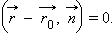 Это – нормальное векторное уравнение прямой, а
Это – нормальное векторное уравнение прямой, а  M и вектор
M и вектор 
 Обозначив
Обозначив  окончательно имеем
окончательно имеем Назовем это уравнение общим уравнением прямой. Следовательно, для любой прямой, заданной общим уравнением Ax + By + C = 0, можно считать, что вектор
Назовем это уравнение общим уравнением прямой. Следовательно, для любой прямой, заданной общим уравнением Ax + By + C = 0, можно считать, что вектор  параллелен ей. Действительно, так как
параллелен ей. Действительно, так как  векторы
векторы  – направляющий вектор прямой,
– направляющий вектор прямой,  предположим для определенности, что A ≠ 0. Тогда точка
предположим для определенности, что A ≠ 0. Тогда точка  принадлежит прямой. В этом легко убедиться, подставив координаты точки в уравнение прямой. Приведенных данных достаточно, чтобы получить векторные уравнения прямой. Действительно,
принадлежит прямой. В этом легко убедиться, подставив координаты точки в уравнение прямой. Приведенных данных достаточно, чтобы получить векторные уравнения прямой. Действительно, – векторно-параметрическое уравнение;
– векторно-параметрическое уравнение;
 – векторное нормальное уравнение.
– векторное нормальное уравнение.
 , числа
, числа  называются компонентами арифметического вектора.
называются компонентами арифметического вектора. для любых
для любых  и
и  и любого числа
и любого числа 
 называется нулевым вектором, а вектор
называется нулевым вектором, а вектор  — противопо
— противопо из Rn и любых чисел α , β справедливо:
из Rn и любых чисел α , β справедливо: , сложение коммутативно;
, сложение коммутативно; ,сложение ассоциативно;
,сложение ассоциативно;
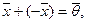
 , умножение на число ассоциативно;
, умножение на число ассоциативно;  ;
; , умножение на число дистрибутивно относительно сложения элементов;
, умножение на число дистрибутивно относительно сложения элементов; , умножение вектора на число дистрибутивно относительно сложения чисел.
, умножение вектора на число дистрибутивно относительно сложения чисел. и
и  из L и любого числа a справедливо
из L и любого числа a справедливо  , называется линейным подпространством в Rn.
, называется линейным подпространством в Rn. 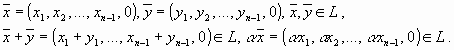
 из L линейно независимы, то для любого
из L линейно независимы, то для любого  существует единственный набор чисел
существует единственный набор чисел  таких, что
таких, что 