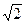|
|
с) Решаем систему методом обратной матрицы.А) Решаем систему методом Гаусса. Расширенная матрица системы имеет вид: Переставим местами две первые строки матрицы. Добиваемся, чтобы под главной диагональю матрицы были только нули. Так в первом столбце уже имеется один ноль. Добьемся, чтобы вместо двойки в первом столбце стоял ноль. Для этого нужно первую строку нужно умножить на (-2) и прибавить к третьей, записывая результат сложения в третью строку имеем: Таким образом, первое действие метода Гаусса выполнено – имеем в первом столбце матрицы все нули. Вторым действием добиваемся, чтобы под главной диагональю второго столбца также был ноль. Для этого третью строку умножаем на (2) и прибавляем ко второй, записывая результат сложения в третью строку: Матрица приведена к треугольному виду. Для получения решения системы, удобно новой расширенной матрице Решаем систему, начиная с третьего уравнения: 3в) Решаем систему методом Крамера. Построим определитель Поскольку найденный определитель не равен нулю, система может быть решена методом Крамера. Построим определитель Аналогично для переменных y и z также строим соответствующие определители: По найденным определителя находим решение системы по формулам с) Решаем систему методом обратной матрицы. Для левой части системы построим матрицу коэффициентов Ее определитель не равен нулю ( Представим нашу систему в матричной форме: Введем еще две матрицы, соответствующие неизвестным x, y, z и столбцу свободных членов в правой части системы: то система, записанная в матричной форме , может быть представлена в компактной форме Умножим слева это матричное уравнение на обратную матрицу Таким образом неизвестную матрицу где в числителе имеется транспонированная ассоциированная матрица ( матрица алгебраических дополнений матрицы Таким образом, имеем:
Пример 4. Решить систему уравнений
Решение проводим методом Гаусса. Расширенную матрицу системы приводим к треугольному виду (четвертое уравнение сделаем первым): Ввиду того, что четвертая строка совпадает с третьей, третье и четвертые уравнения системы совпадают. Отбросим одно из них и запишем соответствующую систему уравнений: Решение системы представим в матричной форме: Таким образом, четырехмерный вектор решения разложен по базису из двух векторов, первый из которых является частным решением первоначальной системы уравнений (легко проверить подстановкой вектора в систему), а второй является решением соответствующей однородной системы уравнений (легко проверяется также подстановкой его в однородную систему уравнений – систему, у которой справа стоят нули). Задача 5. Для заданных векторов:
a=(-1,2,3); b=(0-2,1); c=2i+3j-2k; d=-2j+k; m=(1,-2,-3); p=(-2,0,1) ; n=(0,1,2) и пространственных точек:
A(0,-1,2); B(2,3,-1); C(2,0,0); D(1,1,1); E(0,2,3); F(1,-1,0); G(2,0,3)
упростить и вычислить выражения (N-номер варианта):
a) (Na+b-c) b) a(N-10)(b+m-2p)+a+2b-c-AE+(FG/FG)(Nc-d+k); c) найти угол между векторами EFи (с+Nd).
d) проверить справедливость формулы a Примечание: Вектора обозначаются жирным шрифтом, а модули векторов - нежирным.
Пример 6. Для заданных векторов и пространственных точек упростить выражения:(a-2 b)(a +2b)+|AB где a=i+3j +2k; b=(1, -3, 2); A(2,0,1); B(0,-1,-3)/
Вычислим первое слагаемое: используя свойства скалярного произведения векторов, имеем (a-2b)(a+2b)= AB Подставляем найденные множители в искомое выражение, получаем:
Пример 7. Разложить вектор Разложение ищем в виде: Решая систему, получаем искомые коэффициенты:
Пример 8. На плоскости a) найти три точки A, B, C, b) через них провести прямую AB, c) найти расстояние от точки C до прямой AB. d) Найти точку пересечения прямой L , заданной двумя плоскостями L: e) Найти каноническое уравнение прямой L и g) угол между нормалью к плоскости
a) Для нахождения точки A положим, например b) Каноническое уравнение прямой АВ: c) Для нахождения расстояния от точки С до прямой AB через точку С проведем плоскость Найдем точку К, лежащую на пересечении прямой АВ и плокости Ввиду того, что точка К совпадает с точкой С , точкам С принадлежит прямой АВ и, следовательно, искомое расстояние равно нулю ( это можно было заметить сразу, если подставить координаты точки С в уравнение АВ. d) Найдем точку пересечения М прямой L и плоскости е) Каноническое уравнение прямой L можно построить, если знать одну точку прямой и направляющий вектор прямой Найдем точку Р прямой L: Положим, например Направляющий вектор прямой L найдем как векторное произведение векторов нормалей к плоскостям, образующим прямую L. Таким образом, Каноническое уравнение прямой L можно теперь записать: L: f) Угол между нормалью к плоскости
Пример 9. Сделать схематический рисунок поверхностей второго порядка А)
Решение: А) Приведем поверхность к каноническому виду, для чего выделим полный квадрат по переменной х: Сделаем параллельный перенос осей координат, введя новые переменные: при уравнение поверхности в новой системе координат принимает канонический вид: Найдем координаты точки
Сделаем схематический рисунок поверхности в штрихованной системе координат, воспользовавшись методом сечений: 1. Рассекаем поверхность плоскостью 2. Рассекаем поверхность плоскостью Ввиду того, что два основных сечения –параболы, поверхность называется параболоидом. Тип параболоида определим, сделав третье сечение. 3. Рассекаем поверхность плоскостью По третьему сечению определяем тип параболоида как гиперболический. Таким образом, название поверхности:
P
В) Приведем поверхность к каноническому виду, выделяя полный квадрат по переменной y: Сделаем параллельный перенос осей координат В новой системе координат уравнением поверхности будет Начало новой системы координат
х
Построим поверхность в новой в новой системе координат методом сечений. 1. Рассекаем поверхность плоскостями 2. Рассекаем поверхность плоскостью Из Рис. 3видно, что поверхность представляет собой конус, в горизонтальных сечениях которого располагаются эллипсы,таким образом, название поверхности : КОНУС ЭЛЛИПТИЧЕСКИЙ.
э
э 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. .
. .
. .
. поставить в соответствие систему уравнений:
поставить в соответствие систему уравнений:
 .
. , соответствующей левой части системы уравнений:
, соответствующей левой части системы уравнений:
 .
. , соответствующий
, соответствующий  -ому столбцу определителя, для этого в определителе
-ому столбцу определителя, для этого в определителе  .
. .
. .
. .
. ) т. е матрица А не является вырожденной матрицей, следовательно система может быть решена методом обратной матрицы.
) т. е матрица А не является вырожденной матрицей, следовательно система может быть решена методом обратной матрицы. .
. ,
, .
. , тогда с учетом, что
, тогда с учетом, что 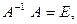 где
где 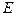 -единичная матрица, имеем:
-единичная матрица, имеем: .
. можно вычислить, если будет известна обратная матрица
можно вычислить, если будет известна обратная матрица  ,
, ).
). Решение системы записывается в виде
Решение системы записывается в виде .
.
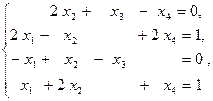 .
.

 .
. (Nn-2p+a-b+c)+AB
(Nn-2p+a-b+c)+AB  +2ab-2ab-
+2ab-2ab- 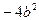

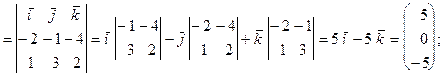
 |i+2j-k|=
|i+2j-k|=  .
.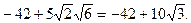
 по базису
по базису  где векторы
где векторы 
 где
где  неизвестные коэффициенты. Найдем их, составив матричное уравнение, а из него систему уравнений:
неизвестные коэффициенты. Найдем их, составив матричное уравнение, а из него систему уравнений:
 откуда разложение вектора по базису принимает вид:
откуда разложение вектора по базису принимает вид:
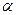 :
: 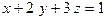
 и плоскости
и плоскости  тогда значение
тогда значение  найдем из уравнения плоскости
найдем из уравнения плоскости  Итак, A(1,0,0). Аналогично найдем точки В(2,1,-1); С(-1,1,0).
Итак, A(1,0,0). Аналогично найдем точки В(2,1,-1); С(-1,1,0).
 , перпендикулярную прямой АВ, затем найдем точку пересечения К этой плоскости с прямой АВ, тогда искомое расстояние будет равно расстоянию между точками К и С.
, перпендикулярную прямой АВ, затем найдем точку пересечения К этой плоскости с прямой АВ, тогда искомое расстояние будет равно расстоянию между точками К и С.



 тогда координаты точки
тогда координаты точки  найдем из системы уравнений L:
найдем из системы уравнений L:



 -вектор нормали к плоскости
-вектор нормали к плоскости  направляющий вектор прямой L:
направляющий вектор прямой L: .
. В)
В) 
 .
. ,
,
 - начала новой штрихованной системы координат. Для чего приравняем координаты
- начала новой штрихованной системы координат. Для чего приравняем координаты  нулю:
нулю: 
 Взаимное расположение осей координат можно представить на рисунке 1.
Взаимное расположение осей координат можно представить на рисунке 1. 










 Рис. 1
Рис. 1 

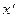
 , в сечении получаем уравнение параболы
, в сечении получаем уравнение параболы  , которую обозначим на рисунке как
, которую обозначим на рисунке как  .
. , в сечении получаем опять параболу
, в сечении получаем опять параболу  , обозначенную на рисунке
, обозначенную на рисунке  .
. в сечении получаем гиперболу
в сечении получаем гиперболу  , обозначенную на рисунке g.
, обозначенную на рисунке g.


 ПАРАБОЛОИД ГИПЕРБОЛИЧЕСКИЙ. Сделаем его рисунок.
ПАРАБОЛОИД ГИПЕРБОЛИЧЕСКИЙ. Сделаем его рисунок. 

 g P
g P 






 Рис.2
Рис.2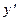

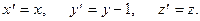



 откуда
откуда 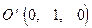 . Взаиморасположение осей координат см. на Рис. 3.
. Взаиморасположение осей координат см. на Рис. 3. 


 Рис. 3
Рис. 3  , получаем в сечениях одинаковые эллипсы с уравнением
, получаем в сечениях одинаковые эллипсы с уравнением  , обозначенные на Рис. 3 э
, обозначенные на Рис. 3 э 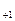 и э
и э  получаем в сечении пару прямых:
получаем в сечении пару прямых:  , обозначенные на Рис. 3P
, обозначенные на Рис. 3P 



 Рис. 4
Рис. 4


 Р
Р