Решение однородных систем.
Теорема Кронекера – Капели.
Пусть дана система из m –уравнений и n – неизвестных
 (1) (1)
В частном случае если m = n и detA ≠ 0, система совместна, имеет единственное решение и оно находится матричным способом, методом Крамера или методом Гаусса.
В общем случае возникает вопрос о ее совместности. Ответ на него дает теорема Кронекера – Капелли. Введем основную и расширенную матрицы системы.
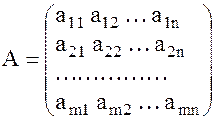 - основная матрица; - основная матрица;

- расширенная матрица.
Теорема(Кронекера – Капелли). Для совместности системы линейных алгебраических уравнений необходимо и достаточно чтобы ранг основной матрицы системы равнялся рангу расширенной матрицы  . .
Замечание:Ранг матрицы системы не может быть больше ранга основной матрицы.
Согласно теореме Кронекера – Капелли если ранг основной матрицы системы меньше ранга расширенной матрицы, то система не совместна.
Решение систем линейных уравнений методом Гаусса.
Рассмотрим случаи для системы размерности  : :
1. Пусть ранг равен числу неизвестных  . Поскольку число уравнений такой системы n равно рангу системы r, то система имеет единственное решение, которое можно найти известными методами (матричным, Крамера) или Гаусса. . Поскольку число уравнений такой системы n равно рангу системы r, то система имеет единственное решение, которое можно найти известными методами (матричным, Крамера) или Гаусса.
Суть метода Гаусса состоит в том, что путем элементарных преобразований из всех уравнений системы, кроме первого, исключаем неизвестное  , далее из всех уравнений системы, кроме первого и второго, исключаем неизвестное , далее из всех уравнений системы, кроме первого и второго, исключаем неизвестное  , и т. д. , и т. д.
Пример. Решить систему.
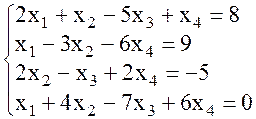
Запишем расширенную матрицу системы, поменяв местами 1 - е и 2 – е уравнение  -это значение учитывается при подсчете определителя), получим: -это значение учитывается при подсчете определителя), получим:
= =
=
Матрица имеет диагональный вид. Определитель  , значит , значит  , ранг равен числу неизвестных , ранг равен числу неизвестных  =4 - единственное решение. Согласно полученной матрице запишем систему эквивалентную исходной: =4 - единственное решение. Согласно полученной матрице запишем систему эквивалентную исходной:
 Применим обратный ход метода Гаусса. Применим обратный ход метода Гаусса.
Из последнего уравнения  найдем найдем 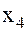 =1 и подставим в 3-е уравнение, найдем =1 и подставим в 3-е уравнение, найдем 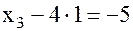 , получим , получим  . Подставим . Подставим  и и  во 2-е уравнение во 2-е уравнение  , или , или  и окончательно из первого уравнения и окончательно из первого уравнения  или или  . Получили единственное решение системы. . Получили единственное решение системы.
Решение произвольных систем линейных уравнений.
Рассмотрим систему линейных уравнений (1)
 (1) (1)
Частный случай если m = n и detA ≠ 0, мы рассмотрели выше. В общем случае, когда система имеет размерность (m  n) возникает вопрос о ее совместности. Ответ на него дает теорема Кронекера – Капелли. n) возникает вопрос о ее совместности. Ответ на него дает теорема Кронекера – Капелли.
Рассмотрим следующие случаи для системы размерности  : :
1. Пусть ранг равен числу неизвестных  . В этом случае система имеет единственное решение. Из теоремы о ранге это означает, что система имеет r = nлинейно-независимых строк. Тогда рассматривают систему, состоящую из nуравнений. Ее можно решить известными уже методами (матричным, Крамера или Гаусса). Остальные m-nуравненийможно отбросить. . В этом случае система имеет единственное решение. Из теоремы о ранге это означает, что система имеет r = nлинейно-независимых строк. Тогда рассматривают систему, состоящую из nуравнений. Ее можно решить известными уже методами (матричным, Крамера или Гаусса). Остальные m-nуравненийможно отбросить.
2. Если  система в этом случае имеет множество решений. Оставляют только rуравнений. Остальные m-r уравнений отбрасывают. В оставленных rуравнениях слева оставляют те неизвестные, коэффициенты при которых вошли в базисный минор. Остальные неизвестные n-r переносят вправо и считают их свободными. система в этом случае имеет множество решений. Оставляют только rуравнений. Остальные m-r уравнений отбрасывают. В оставленных rуравнениях слева оставляют те неизвестные, коэффициенты при которых вошли в базисный минор. Остальные неизвестные n-r переносят вправо и считают их свободными.
Пример. Решить систему. Размерность системы  . .
 видно, что видно, что  тогда по теореме о ранге тогда по теореме о ранге 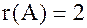 и ранг расширенной матрицы также будет и ранг расширенной матрицы также будет  то есть ранг системы r равен 2. Система совместна по теореме Кронекера - Капелли. Найдем минор второго порядка не равный нулю. то есть ранг системы r равен 2. Система совместна по теореме Кронекера - Капелли. Найдем минор второго порядка не равный нулю.
     выделен базисный минор. выделен базисный минор.
Поскольку r<n (n=4, r=2) то система имеет множество решений.Это соответствует второму случаю, согласно которому оставим r=2 уравнения, одно уравнение (m-r=3-2=1) отбросим. В оставленных уравнениях неизвестные  , коэффициенты при которых вошли в базисный минор, оставим слева, остальные неизвестные , коэффициенты при которых вошли в базисный минор, оставим слева, остальные неизвестные  будем считать свободными. будем считать свободными.
Сложим и найдем  . Затем из первого найдем . Затем из первого найдем  . .
| |   
или  или или  задавая различные значения задавая различные значения  и и 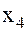 получим множество решений. получим множество решений.
Решение однородных систем.
Опр. Система вида
 называется однородной все bi =0. называется однородной все bi =0.
Однородная система всегда совместна, так как  . Рассмотрим следующие случаи: . Рассмотрим следующие случаи:
1) Если  система имеет единственное решение, называемое тривиальным, то есть нулевым. система имеет единственное решение, называемое тривиальным, то есть нулевым.
2) Если r<n то система имеет бесконечное множество решений.
Пример. Решить систему.
 строки линейно зависимы строки линейно зависимы  следовательно ранг r=2. Так как r<nто система имеет множество решений. Найдем базисный минор следовательно ранг r=2. Так как r<nто система имеет множество решений. Найдем базисный минор
   получим получим  умножим 1-е уравнение на 2 и сложим, получим х, затем 2-е уравнение умножим на (-2) и снова сложим, найдем у. Получим: умножим 1-е уравнение на 2 и сложим, получим х, затем 2-е уравнение умножим на (-2) и снова сложим, найдем у. Получим:  или или  . Задавая различные значения z получим множество решений х и у. . Задавая различные значения z получим множество решений х и у.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|





 (1)
(1)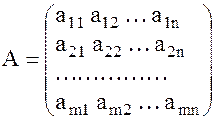 - основная матрица;
- основная матрица;
 .
. :
: . Поскольку число уравнений такой системы n равно рангу системы r, то система имеет единственное решение, которое можно найти известными методами (матричным, Крамера) или Гаусса.
. Поскольку число уравнений такой системы n равно рангу системы r, то система имеет единственное решение, которое можно найти известными методами (матричным, Крамера) или Гаусса. , далее из всех уравнений системы, кроме первого и второго, исключаем неизвестное
, далее из всех уравнений системы, кроме первого и второго, исключаем неизвестное  , и т. д.
, и т. д.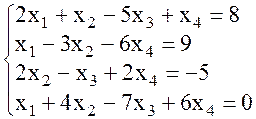
 -это значение учитывается при подсчете определителя), получим:
-это значение учитывается при подсчете определителя), получим:





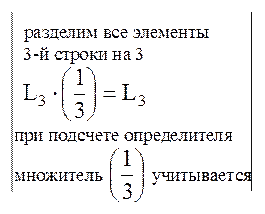




 , значит
, значит  Применим обратный ход метода Гаусса.
Применим обратный ход метода Гаусса. найдем
найдем 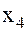 =1 и подставим в 3-е уравнение, найдем
=1 и подставим в 3-е уравнение, найдем 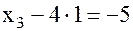 , получим
, получим  . Подставим
. Подставим  во 2-е уравнение
во 2-е уравнение  , или
, или  и окончательно из первого уравнения
и окончательно из первого уравнения  или
или  . Получили единственное решение системы.
. Получили единственное решение системы. n) возникает вопрос о ее совместности. Ответ на него дает теорема Кронекера – Капелли.
n) возникает вопрос о ее совместности. Ответ на него дает теорема Кронекера – Капелли. :
: система в этом случае имеет множество решений. Оставляют только rуравнений. Остальные m-r уравнений отбрасывают. В оставленных rуравнениях слева оставляют те неизвестные, коэффициенты при которых вошли в базисный минор. Остальные неизвестные n-r переносят вправо и считают их свободными.
система в этом случае имеет множество решений. Оставляют только rуравнений. Остальные m-r уравнений отбрасывают. В оставленных rуравнениях слева оставляют те неизвестные, коэффициенты при которых вошли в базисный минор. Остальные неизвестные n-r переносят вправо и считают их свободными. .
. видно, что
видно, что  тогда по теореме о ранге
тогда по теореме о ранге 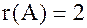 и ранг расширенной матрицы также будет
и ранг расширенной матрицы также будет  то есть ранг системы r равен 2. Система совместна по теореме Кронекера - Капелли. Найдем минор второго порядка не равный нулю.
то есть ранг системы r равен 2. Система совместна по теореме Кронекера - Капелли. Найдем минор второго порядка не равный нулю.



 выделен базисный минор.
выделен базисный минор. , коэффициенты при которых вошли в базисный минор, оставим слева, остальные неизвестные
, коэффициенты при которых вошли в базисный минор, оставим слева, остальные неизвестные  будем считать свободными.
будем считать свободными. или
или  задавая различные значения
задавая различные значения  называется однородной все bi =0.
называется однородной все bi =0. система имеет единственное решение, называемое тривиальным, то есть нулевым.
система имеет единственное решение, называемое тривиальным, то есть нулевым. строки линейно зависимы
строки линейно зависимы  следовательно ранг r=2. Так как r<nто система имеет множество решений. Найдем базисный минор
следовательно ранг r=2. Так как r<nто система имеет множество решений. Найдем базисный минор

 получим
получим  умножим 1-е уравнение на 2 и сложим, получим х, затем 2-е уравнение умножим на (-2) и снова сложим, найдем у. Получим:
умножим 1-е уравнение на 2 и сложим, получим х, затем 2-е уравнение умножим на (-2) и снова сложим, найдем у. Получим:  или
или  . Задавая различные значения z получим множество решений х и у.
. Задавая различные значения z получим множество решений х и у.