|
|
Маршруты и связность в ориентированных графахНеориентированные графы Основные определения
Обозначим
(v1,v2) ~ (w1,w2), если (v1,v2) = (w1,w2) или (v1,v2) = (w2,w1). Множество эквивалентных классов, определенное таким образом, обозначим
, то [(v1,v2)] = {(v1,v2), (v2,v1)}.
Множество E - это множество ребер графа. Обычно в графе всегда можно определить количество вершин |V| и ребер |E|. Граф G определяет нерефлексивное, симметричное отношение на множестве V. Обратное утверждение тоже верно: нерефлексивное, симметричное отношение на множестве V определяет граф. Изображение графа G = (V, E) получается путем расположения различных точек на R2 для каждой вершины v Î V . Причем, если [v, w] Î E, проводим линию, соединяющую вершины v и w. Графы в значительной мере выражают отношения между вершинами, а не их расположение в пространстве. То есть один и тот же граф может быть изображен разными способами (рис. 1).
v1 v3
Рис. 1. Примеры изображения графа
Приведем пример построения графа (рис. 2). Пусть V={1, 2, 3, 4, 5}. Тогда IV = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5)}.
V2 = V ´ V = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5)}
= {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5)}
= {[(v1, v2)], [(v1, v3)], [(v1, v4)], [(v1, v5)], [(v2, v1)], [(v2, v3)], [(v2, v4)], [(v2, v5)], [(v3, v1)], [(v3, v2)], [(v3, v4)], [(v3, v5)], [(v4, v1)], [(v4, v2)], [(v4, v3)], [(v4, v5)], [(v5, v1)], [(v5, v2)], [(v5, v3)], [(v5, v4)]}.
По определению 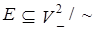 . Следовательно, может быть, что . Следовательно, может быть, что  . В результате получили граф G = (V, E), причем такой, что |V| = 5, |E| = 20. . В результате получили граф G = (V, E), причем такой, что |V| = 5, |E| = 20.
Рис. 2 . Полный граф Граф H = (V1, E1) является подграфом графа G = (V, E), если V1 Í V и E1 Í E. Если V1 = V, то граф H является остовным подграфом графа G. Если V1 – непустое подмножество вершин графа (V, E), то подграф (V1, E1), порожденный V1, определяется как [v, w] Î E1 Û v, w Î V1 и [v, w] Î E. Граф G = (V, E) называется полным, если для всех v1, v2 Î V имеем [v1, v2] Î E. Полный граф с n вершинами обозначается Kn. Граф G = (V, E) называется двудольным, если существует разбиение множества его вершин V = {V1, V2} такое, что никакие две вершины из V1 или из V2 не являются смежными. Двудольный граф называется полным, если для любой пары v1 Î V, v2 Î V имеем [v1, v2] Î E. Если |V1| = m и |V2| = n, то полный двудольный граф G = (V, E) обозначается Km,n.
Маршруты, циклы и связность Значительная часть теории графов и ее приложений занимается вопросами существования и изучения свойств маршрутов в графах. Пусть G = (V, E) – граф. Маршрутом длины k в графе G из вершины v в вершину w называется последовательность <v0, v1, v2, …, vk> вершин (необязательно различных) vi Î V, таких, что v0 = v, vk = w, а [vi-1, vi] Î E для i = 1, …, k. Маршрут называется замкнутым, если v0 = vk. Маршрут называется цепью, если все его вершины различны. Замкнутая цепь называется циклом. Цикл называется простым, если только v0 = vk, а остальные вершины vi различны. Если существует маршрут из v в w, v, w Î V, то говорят, что w достижима из v. Граф без циклов называется ациклическим. Граф G = (V, E) называется связным, если каждая пара различных вершин может быть соединена маршрутом. Деревом называется связный ациклический граф. Корневым деревом называется дерево с выделенной вершиной, называемой корнем. Остовным деревом для G = (V, E) называется остовный подграф, являющийся деревом. Пусть {Vi : 1 £ i £ p} – разбиение графа G = (V, E), определяемое отношением R*. (R* - отношение рефлексивного замыкания). Тогда p – число связности графа G = (V, E). Подграфы (Vi, Ei), порожденные классами эквивалентности, называют компонентами связности графа G.
Ориентированные графы Основные определения Во многих приложениях теории графов требуется, чтобы ребра графа имели направление. Например: поток данных, проходящий через программу. Ориентированный граф G (или просто орграф) есть пара G = (V, E), где V – конечное множество вершин, а E – произвольное подмножество. Ориентированный граф G = (V, E) определяет отношение на V. Этот факт можно доказать следующим образом. Пусть R – отношение, такое, что vRw тогда и только тогда, когда (v, w) Î E. Очевидно, что R является отношением. Обратное утверждение также верно: пусть V – конечное множество вершин. Тогда отношение на V определяет ориентированный граф, у которого множество вершин V. Этот факт можно доказать так. Если R – отношение на V, то орграф G = (V, E), определяемый отношением R, имеет множество ребер E, где (v, w) Î E тогда и только тогда, когда vRw. Направление ребра обозначают порядком в V ´ V. Например, если (v, w) Î E, то ребро выходит из v и входит в w. Приведем пример построения ориентированного графа (рис. 3). Пусть V = {v1, v2, v3}, E1 = {(v1, v2), (v2, v3), (v3, v1)}. Тогда получим граф G1 = (V, E1) (рис. 3, а). Пусть V = {v1, v2, v3}, E2 = {(v1, v1), (v1, v2), (v1, v3), (v2, v3), (v3, v1)}. Тогда получим граф G2 = (V, E2) (рис. 3, б).
а) б) Рис. 3. Примеры ориентированных графов: а – граф G1 = (V, E1); б – граф G2 = (V, E2);
Для орграфа реберное отношение необязательно симметрично или рефлексивно. Поэтому допустимы ребра типа (v, v), называемые петлями. Степень вершины v ÎV обозначается s(v) = s + (v) + s - (v), где s - (v) – число ребер, входящих в v, s + (v) – число ребер, выходящих из v. Множества {w: (w, v) Î E} и {w: (v, w) Î E} называют соответственно входящим узлом и выходящим узлом.
Маршруты и связность в ориентированных графах
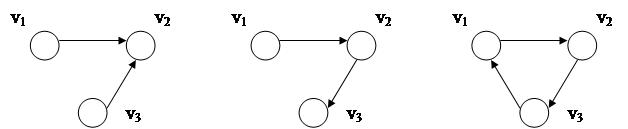
Маршрутом длины k из v в w в орграфе G = (V, E) называется последовательность ребер вида: (v, w1), (w1, w2), (w2, w3), …, (wk-2, wk-1), (wk-1, w), то есть вторая вершина каждого ребра совпадает с первой вершиной следующего ребра. Удобно представлять маршрут в орграфе последовательностью вершин: v, w1, w2, w3, …, wk-2, wk-1, w. Если v = w, то маршрут называют замкнутым маршрутом, или циклом. Орграф без циклов называется ациклическим. Пусть D – множество всех орграфов, а P – множество всех графов вообще. Можно определить отображение F: D ® P следующим образом: Пусть G = (V, E) Î D. Тогда множество вершин F(G) совпадает с V, а множество ребер F(G) определяется применением следующих операций на Е: · удаляются все петли из Е; · (v, w) заменяются на [v, w] для всех (v, w) Î E. Тогда F(G) является графом, связанным с орграфом G. Для орграфов понятие связности является более содержательным, чем для графов, и имеет отношение к проблеме обхода. Определим три важных типа связности орграфа: · G слабо связный, если граф F(G) - связный; · G односторонне связный, если для каждой пары различных вершин v, w, принадлежащей множеству E, существует маршрут из v в w или обратно; · G односторонне связный, если для каждой пары различных вершин v, w, принадлежащей множеству E, существует маршрут из v в w и обратно. Очевидно, что если G – сильно связный орграф, то G - односторонне связный. Если G - односторонне связный орграф, то G слабо связный (рис. 4).
а) б) в) Рис. 4. Типы связности орграфа: а – слабо связный, б – односторонне связный, в – сильно связный
Если {Vi: 1 £ i £ p} – разбиение V и {Ei: 1 £ i £ p, а Ei = (Vi ´ Vi) ìüE} являются соответствующими множествами ребер, то подграфы Gi = (Vi, Ei), 1 £ i £ p называются сильно связными компонентами G. Пусть G = (V, E) – ациклический орграф. Вершину v ÎV называют листом, если s + (v) = 0, то есть отсутствуют исходящие из нее дуги. Если (v, w) Î E, то w является непосредственным потомком v, а v является непосредственным предком w. Если существует маршрут из вершины v в вершину w, то v является предком w, а w – потомком v (рис.5). Эти понятия не имеют смысла для ориентированных графов, имеющих циклы, так как для таких графов вершины могут исходить сами из себя.
Рис. 5. Предки и потомки в ациклическом орграфе: вершины v2 , v4 ,v5 являются листьями, так как из них ребра не выходят; вершина v1 – является предком v5, v5 – прямой потомок v3.
Существует тесная связь между ациклическими орграфами и частично упорядоченными отношениями: · Пусть отношение < является частичным отношением порядка на конечном множестве V. Тогда, если E = {(v, w): v < w}, то пара G = (V, E) является ациклическим ориентированным графом. · Пусть G = (V, E) – ациклический орграф и отношение < определяется следующим образом: v < w, если v является предком w. Тогда отношение < является частичным отношением порядка на V.
Ориентированное дерево T = (V, E) – это ациклических орграф, в котором одна вершина vr Î V не имеет предков, а каждая другая вершина имеет только одного непосредственного предка. Вершина vr называется корнем дерева. Бинарное дерево – это ориентированное дерево, в котором каждая вершина имеет не более двух непосредственных потомков, то есть s + (v) £ 2, " v Î V. Говорят, что бинарное дерево называется полным, если каждая вершина, не являющаяся листом, имеет ровно двух непосредственных потомков. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
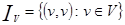 Пусть V – конечное множество некоторых элементов, и IV – его тождественное отношение, такое, что:
Пусть V – конечное множество некоторых элементов, и IV – его тождественное отношение, такое, что:
 Определим отношение эквивалентности следующим образом:
Определим отношение эквивалентности следующим образом: Каждый класс эквивалентности содержит два элемента, так как если
Каждый класс эквивалентности содержит два элемента, так как если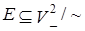 Графом называется упорядоченная пара G = (V, E), где V – непустое конечное множество вершин, а , то есть E - это множество неупорядоченных пар различных вершин.
Графом называется упорядоченная пара G = (V, E), где V – непустое конечное множество вершин, а , то есть E - это множество неупорядоченных пар различных вершин. v1 v2 v3 v2
v1 v2 v3 v2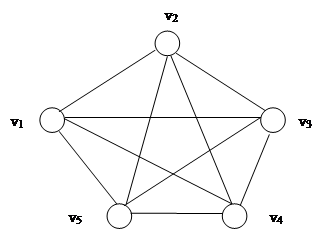
 Лесом называется граф, в котором каждая связная компонента является деревом. Остовный лес для графа G = (V, E) – это совокупность вершин разъединенных деревьев Ti = (Vi, Ei):
Лесом называется граф, в котором каждая связная компонента является деревом. Остовный лес для графа G = (V, E) – это совокупность вершин разъединенных деревьев Ti = (Vi, Ei):