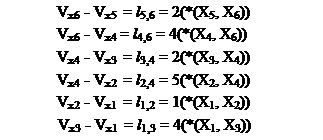|
|
Волновой алгоритм построения кратчайшего пути для взвешенного графа1. Вершина Хн получает вес V = 0, ее номер вводится в массив М номеров 2. Если массив M пуст, то выполняется п. 3, иначе выбирается с исключением 3. Если вес Vi = ∞, то делается вывод, что пути из вершины Хн к вершине Xk
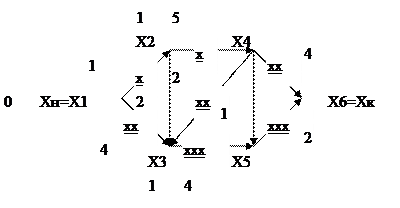
1. Vi = V1 = 0, V2 = V3 = V4 = V3 = V6 = ∞, M = {1} 2. M ≠ 0, i = 1, M = 0, G(X1) = {X2, X3}; V2 = min (∞, 0 + 1)=1; M ={2} Vi = min (∞, 0 + 4) = 4; M ={2,3}; 2. M ≠ 0, i = 2, M = {3}, G(X2) = {X3, X4}; V3 = min (4, 1 + 2)=3; M = {3}; V4 = min (∞, 1 + 5) = 6; M={3,4}; 2. M ≠ 0, i = 3, M = {4}, G(X3) = {X4, X5}; V4 = min (6, 3 + 2)=5; M = {4}; V5 = min (∞, 3 + 4) = 7; M={4,5}; 2. M ≠ 0, i = 4, M = {5}, G(X4) = {X5, X6}; V5 = min (7, 5 + 1)=6; M = {5}; V6 = min (∞, 5 + 4) = 9; M={5,6}; 2. M ≠ 0, i = 5, M = {6}, G(X6) = {X6}; V6 = min (9, 6 + 2)=8; M = {6}; 2. M ≠ 0, i = 6, M = {0}, G(6) = {0}; 3. G-1(X6) = {X4, X5}; Vx6 - Vx5 = 2; l6 = 2,* Vx6 - Vx4 = 3, l4,6 = 4. G-1(X5) = {X3, X4}; Vx5 - Vx4 = 1; l4,5 = 1,* Vx5 - Vx3 = 3, l5,3 = 4. G-1(X4) = {X2, X3}; Vx4 - Vx3 = 2; l3,4 = 2,* Vx4 - Vx2 = 4, l2,4 = 5. G-1(X3) = {X1, X2}; Vx3 - Vx2 = 2; l2,3 = 2,* Vx3 - Vx1 = 3, l1,3 = 4. G-1(X2) = {X1}; Vx2 - Vx1 = 1; l1 = 1,* Построен кратчайший путь (Xн, Xк) длиной 8: (Xн = Х1, Х2)( Х2, Х3)( Х3, Х4)( Х4, Х5)( Х5, Х6 = Хк). Процесс решения можно оформить в виде таблицы:
Волновой алгоритм построения длиннейшего пути во взвешенном графе
Используется волновой алгоритм построения кратчайшего пути для взвешенного графа со следующим отличием: 1. В первом пункте волнового алгоритма нужно присвоить всем вершинам вес 0, 2. Во втором пункте алгоритма Vj = max (Vj, Vi + lij)
Обратный ход:
Построены три длиннейшие пути: 1. (Х1, Х2)( Х2, Х4)( Х4, Х6) 2. (Х1, Х3)( Х3, Х4)( Х4, Х6) 3. (Х1, Х3)( Х3, Х5)( Х5, Х6) Алгоритм нахождения компонент связанности Вершины Хi и Xj слабо связны, если существует путь (Хi и Xj) в графе (G,X). Вершины Xi и Xj сильно связаны, если существуют пути (Хi и Xj)и (Xj и Хi) в графе (G, X). Если в графе нет путей Хi и Xjи нет обратного пути из Хj в Xi, то вершины Хi и Xj не связаны. Для неориентированною графа имеет смысл только понятие сильной связности. Отношение связности рефлексивно, симметрично, транзитивно - является отношением эквивалентности и однозначно разбивает множество вершим графа на компоненты связности: максимальные подмножества сильно связанных между собой вершин. Пример 3.2.1
Компоненты связности: 1) {x1, x2, x3, x4}; 2) {x5, x6, x7}; 3) {x8}. Между компонентами - только слабая связность: есть пути из вершин компоненты 1) в вершины компоненты 2) и 3) и из вершин компоненты 2) в 3). Алгоритм построения компонент связности в неориентированном графе 1. i=0. Все вершины графа не отмечены. 2. i=i+1. Выбираем очередную неотмеченною вершину, отмечаем ее и все
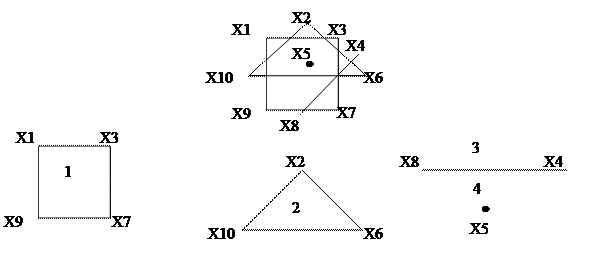
Пример 3.2.2 1.i = 0 2. i = 1. Отмечаем индексом i =1 вершину Х1, и связанные с ней вершины Х3, Х7, Х9. Получена первая компонента связности: 1{ Х1, Х3, Х7, Х9}. 3. i =2. Отметим индексом i = 2 вершину Х4 и вершины Х6, Х10. Построена вторая компонента связности: 2{ Х2, Х6, Х10) 4. i=3 Отмечаются индексом i = 3 вершины X4 и Х8. Построена третья компонента связности: 3{X4, X8}. 5. i=4. Отметим индексом i = 4 вершину Х5, которая формирует четвертую компоненту связности -{X5}. Дерево. Остов.
Рис.3 Остов – это подграф (частичный), который может быть построен из графа удалением некоторых ребер и который является деревом.
В общем случае для графа можно построить несколько остовов. Для приведенного ниже графа построен один из возможных вариантов остова.
Для несвязного графа рассматриваются отдельные его компоненты. Остов такого графа – совокупность его компонент. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 4. После выделения дуг строятся кратчайшие пути, длины которых равны Vk.
4. После выделения дуг строятся кратчайшие пути, длины которых равны Vk.