Метод оптимального исключения
Существенное достоинство этого метода состоит в том, что он позволяет решать системы более высокого порядка при одних и тех же затратах оперативной памяти. Предположим, что после преобразования первых 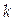 уравнений матрица преобразованной системы имеет вид уравнений матрица преобразованной системы имеет вид
 (4.10) (4.10)
Исключим неизвестные  из из  -го уравнения с помощью -го уравнения с помощью 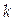 первых уравнений и разделим полученное уравнение на коэффициент, стоящий при первых уравнений и разделим полученное уравнение на коэффициент, стоящий при  . .
С помощью полученного уравнения исключим  из из 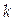 первых уравнений системы. В результате получаем систему с матрицей (4.10), но с заменой индекса первых уравнений системы. В результате получаем систему с матрицей (4.10), но с заменой индекса 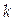 на на  . Все вычисления в методе оптимального исключения проводятся по формулам . Все вычисления в методе оптимального исключения проводятся по формулам
 , ,
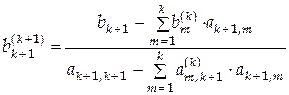
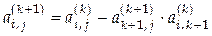 , ,
  , , 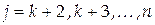 . .
После преобразования всех уравнений находим решение исходной системы
 , ,  . .
Для решения системы уравнений  -го порядка по методу оптимального исключения необходимо выполнить ровно столько операций умножения и деления, как и в схеме единственного деления Гаусса. -го порядка по методу оптимального исключения необходимо выполнить ровно столько операций умножения и деления, как и в схеме единственного деления Гаусса.
Метод Гаусса с выбором главного элемента
Иногда может оказаться, что система (4.1) имеет единственное решение, хотя какой-либо из главных миноров матрицы  равен нулю. Кроме того, заранее неизвестно, все ли главные миноры матрицы отличны от нуля. В этих случаях обычный метод Гаусса может оказаться непригодным так, как в процессе вычисления какой-то ведущий элемент равен нулю. Кроме того, заранее неизвестно, все ли главные миноры матрицы отличны от нуля. В этих случаях обычный метод Гаусса может оказаться непригодным так, как в процессе вычисления какой-то ведущий элемент 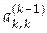 станет равным нулю. Кроме того, если на главной диагонали элемент станет равным нулю. Кроме того, если на главной диагонали элемент 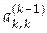 мал, то деление на этот элемент приводит к значительным ошибкам округления. Избежать указанных трудностей позволяет метод Гаусса с выбором главного элемента. В этом методе исключается не следующее по порядку неизвестное, а то неизвестное, коэффициент при котором является наибольшим по модулю. При применении такого варианта метода Гаусса не будет происходить деление на нуль. Различают три варианта метода Гаусса с выбором главного элемента: мал, то деление на этот элемент приводит к значительным ошибкам округления. Избежать указанных трудностей позволяет метод Гаусса с выбором главного элемента. В этом методе исключается не следующее по порядку неизвестное, а то неизвестное, коэффициент при котором является наибольшим по модулю. При применении такого варианта метода Гаусса не будет происходить деление на нуль. Различают три варианта метода Гаусса с выбором главного элемента:
а) метод Гаусса с выбором главного элемента по строке: в системе на каждом шаге исключения проводится соответствующая перенумерация переменных;
б) метод Гаусса с выбором главного элемента по столбцу: на каждом шаге исключения проводится перенумерация уравнений;
в) метод Гаусса с выбором главного элемента во всей матрице системы: в этом случае проводится перенумерация и переменных и уравнений.
С точки зрения программной реализации вариант б) является более привлекательным, так как он не требует перенумерации переменных, что приводит к потере однородности вычислительного процесса. Метод Гаусса с выбором главного элемента позволяет уменьшить погрешность округления, но при решении плохо обусловленных систем устойчивость этого метода может оказаться недостаточной.
ЛЕКЦИЯ № 9
Методы, основанные на разложении матриц
Схема Холецкого
Используем для решения системы (4.1) теорему о разложении невырожденной квадратной матрицы в произведение нижней и верхней треугольных матриц.
Теорема 4.1.Если главные миноры матрицы  отличны от нуля: отличны от нуля:
 , ,  , …, , …,  , ,
то матрица  представима в виде представима в виде
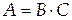 , (4.11) , (4.11)
где  и и  - соответственно нижняя и верхняя треугольные матрицы. - соответственно нижняя и верхняя треугольные матрицы.
Разложение (4.11) не может быть единственным. Если взять произвольную диагональную матрицу  , с элементами, отличными от нуля, то вместе с равенством , с элементами, отличными от нуля, то вместе с равенством 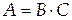 справедливо также равенство справедливо также равенство  . Поэтому диагональные элементы одной из матриц . Поэтому диагональные элементы одной из матриц  и и  можно задавать произвольными, отличными от нуля. можно задавать произвольными, отличными от нуля.
Зафиксируем элементы главной диагонали матрицы  , положив , положив  , ,  . В этом случае разложение имеет вид . В этом случае разложение имеет вид
 (4.12) (4.12)
Учитывая разложение (4.11), система (4.1) принимает вид  . Тогда вектор неизвестных . Тогда вектор неизвестных  можно найти из цепочки матричных уравнений можно найти из цепочки матричных уравнений
 , ,  (4.13) (4.13)
Вектор  находится из системы с нижней треугольной матрицей находится из системы с нижней треугольной матрицей

по формулам  , ,  , ,  . Определив вектор . Определив вектор  , находим , находим
вектор неизвестных из системы с верхней треугольной матрицей
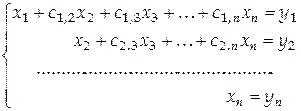
Вычисление проводится по формулам, аналогичным формулам для обратного хода схемы единственного деления Гаусса
 , , 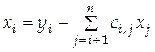 , , 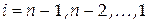 . .
Описанный метод решения систем линейных алгебраических уравнений называется схемой Холецкого.
Метод квадратного корня
Этот метод используется для решения систем линейных алгебраических уравнений с эрмитовой невырожденной матрицей  . Матрица . Матрица  называется эрмитовой, если она совпадает со своей комплексно-сопряженной транспонированной матрицей, т.е. называется эрмитовой, если она совпадает со своей комплексно-сопряженной транспонированной матрицей, т.е.  . Среди прямых методов этот метод является самым быстродействующим и особенно удобен для решения систем уравнений с ленточной матрицей, у которой . Среди прямых методов этот метод является самым быстродействующим и особенно удобен для решения систем уравнений с ленточной матрицей, у которой  при при  , где , где 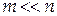 . .
Будем искать разложение действительной матрицы  системы (4.1) в виде системы (4.1) в виде
 , (4.14) , (4.14)
где
 , ,
 - диагональная матрица с элементами - диагональная матрица с элементами  . .
После перемножения матриц получаем
 , ,  , ,
 , ,  . .
Потребуем, чтобы элементы  были положительными числами. Тогда получим были положительными числами. Тогда получим
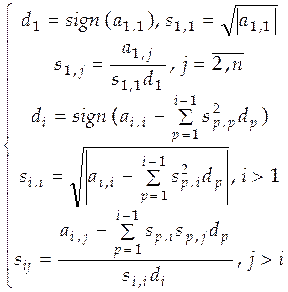 (4.15) (4.15)
Таким образом, разложение (4.14) существует и определяется формулами (2.15). Тогда решение системы (4.1) сводится к решению двух систем с треугольными матрицами
 , ,  . .
Первая система имеет вид
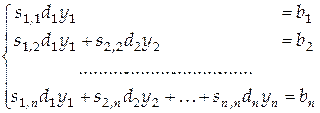
и ее решение находится по формулам
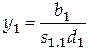 , ,  , ,  . .
Вторая система

дает решение исходной системы (4.1)
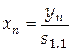 , ,  , , 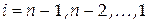 . .
Если матрица  является положительно определенной (все главные миноры положительны), то является положительно определенной (все главные миноры положительны), то  и и  . Формулы разложения имеют в этом случае вид . Формулы разложения имеют в этом случае вид
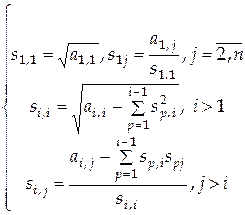
Для решения системы линейных алгебраических уравнений с вещественной матрицей порядка  методом квадратного корня необходимо выполнить методом квадратного корня необходимо выполнить  операций умножения и деления и операций умножения и деления и  извлечений квадратного корня. извлечений квадратного корня.
ЛЕКЦИЯ № 10
Метод отражений
Этот метод основан на разложении матрицы  системы (4.1) в произведение унитарной матрицы на верхнюю треугольную. Матрица системы (4.1) в произведение унитарной матрицы на верхнюю треугольную. Матрица  называется унитарной, если она удовлетворяет уравнению называется унитарной, если она удовлетворяет уравнению  , где , где  - матрица, сопряженная с - матрица, сопряженная с  . Вещественные унитарные матрицы называются ортогональными. . Вещественные унитарные матрицы называются ортогональными.
По своей структуре метод отражений близок к методу Гаусса, но исключение проводится с помощью матриц отражения, которые являются унитарными и эрмитовыми. Достоинством метода отражений является единая схема вычислительного процесса, не зависящая от структуры матрицы.
Теорема 4.2. Пусть  и и  произвольные вектор-столбцы, причем вектор произвольные вектор-столбцы, причем вектор  имеет единичную длину. Тогда найдется такой вектор имеет единичную длину. Тогда найдется такой вектор  , что построенная по нему матрица отражения , что построенная по нему матрица отражения  переведет вектор переведет вектор  в вектор, коллинеарный вектору в вектор, коллинеарный вектору  , т.е. , т.е.  . .
Вектор  строится по правилу строится по правилу
 , (4.16) , (4.16)
где  , ,  , ,  . .
Будем преобразовывать расширенную матрицу систему по правилу
 , , 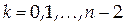
с помощью умножения слева на последовательность матриц отражения  . Для построения матрицы . Для построения матрицы  на первом шаге метода в качестве вектора на первом шаге метода в качестве вектора  берется первый столбец расширенной матрицы, а в качестве вектора берется первый столбец расширенной матрицы, а в качестве вектора  - координатный вектор - координатный вектор  . В силу выбора векторов . В силу выбора векторов  и и  все координаты первого столбца расширенной матрицы, кроме первой, после выполнения первого шага метода будут равны нулю. все координаты первого столбца расширенной матрицы, кроме первой, после выполнения первого шага метода будут равны нулю.
Пусть уже построена матрица  , у которой , у которой  , ,  , ,  . Теперь в качестве . Теперь в качестве  и и  берутся вектора берутся вектора
 , ,  , ,
где в векторе  единица стоит на единица стоит на  -ом месте. После выполнения -ом месте. После выполнения 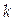 -го шага метода отражений получим матрицу -го шага метода отражений получим матрицу  , у которой все элементы, стоящие ниже главной диагонали, в первых , у которой все элементы, стоящие ниже главной диагонали, в первых  -ом столбцах будут равны нулю. Невозможность выполнения очередного шага связана только с равенством нулю вектора -ом столбцах будут равны нулю. Невозможность выполнения очередного шага связана только с равенством нулю вектора  , а это невозможно, так как матрица , а это невозможно, так как матрица  является невырожденной. является невырожденной.
После  - шага получим матрицу, первые - шага получим матрицу, первые  столбцов которой образуют верхнюю треугольную матрицу столбцов которой образуют верхнюю треугольную матрицу  . Система уравнений, соответствующая полученной расширенной матрице, равносильна исходной системе (4.1). Значения неизвестных находятся аналогично обратному ходу метода Гаусса . Система уравнений, соответствующая полученной расширенной матрице, равносильна исходной системе (4.1). Значения неизвестных находятся аналогично обратному ходу метода Гаусса
 , ,  , , 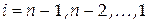
Для решения системы линейных алгебраических уравнений методом отражений необходимо выполнить  операций умножения и деления, а также операций умножения и деления, а также  извлечений квадратных корней. извлечений квадратных корней.
Пример.
Решить систему линейных алгебраических уравнений методом отражений
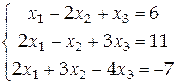
Решение: По системе уравнений составим матрицу
 . .
Шаг 1.  , ,  , ,  , ,  , ,
 , ,  , ,  , ,
 , ,
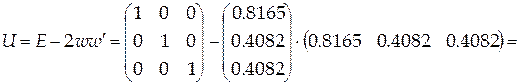
 . .
Тогда  . .
Шаг 2.  , ,  , ,  , ,  , ,
 , ,  , ,  , ,
 , ,
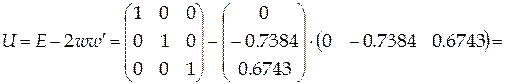
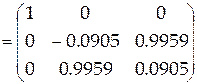 . .
Тогда  . .
Шаг 3.Исходная система преобразована к системе с верхней треугольной матрицей. Пользуясь обратным ходом метода Гаусса, находим , ,  , ,  . .
Метод вращений
Вещественные унитарные матрицы
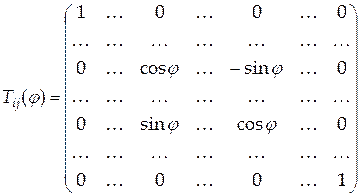
называются элементарными матрицами вращения или матрицами простого поворота. При умножении матрицы  слева на матрицу слева на матрицу  получим матрицу получим матрицу  , у которой изменятся в отличие от матрицы , у которой изменятся в отличие от матрицы  только только  -я и -я и  -я строки. Изменение элементов -я строки. Изменение элементов  -й и -й и  -й строк осуществляется по формулам -й строк осуществляется по формулам
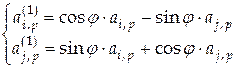 , ,  . (4.17) . (4.17)
Всегда можно подобрать угол поворота  так, чтобы элемент так, чтобы элемент  оказался равным нулю. Для этого нужно взять оказался равным нулю. Для этого нужно взять
 , ,  , (4.18) , (4.18)
если  , и , и  , , 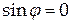 в противном случае. в противном случае.
Теорема 4.3.Любая действительная матрица преобразуется в верхнюю треугольную матрицу после умножения слева на конечную цепочку матриц простого поворота  . .
Рассмотрим систему (4.1) и построим для матрицы  системы унитарную матрицу системы унитарную матрицу  так, чтобы матрица так, чтобы матрица  преобразованной системы стала верхней треугольной. Тогда система преобразуется к виду преобразованной системы стала верхней треугольной. Тогда система преобразуется к виду
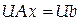 . .
Матрица  представляет собой произведение унитарных матриц простого поворота представляет собой произведение унитарных матриц простого поворота  . Матрица . Матрица  строится так, чтобы после умножения обнулить элемент строится так, чтобы после умножения обнулить элемент  , стоящий под главной диагональю. В этом случае угол поворота выбирается по формулам (4.18). , стоящий под главной диагональю. В этом случае угол поворота выбирается по формулам (4.18).
Пример.
Решить систему линейных алгебраических уравнений методом вращений.
 . .
Решение: По системе уравнений составим матрицу
 . .
Шаг 1. В матрице  обнулим элемент обнулим элемент  . Для этого возьмем . Для этого возьмем  , ,  , ,  и построим матрицу вращений и построим матрицу вращений  . Получаем . Получаем
 , ,  , ,
 . .
Тогда  . .
Шаг 2. Обнулим элемент 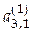 в матрице в матрице  . Для этого берем . Для этого берем  , , 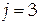 , ,  и строим матрицу и строим матрицу 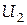 . Имеем . Имеем
 , ,  , ,
 , ,
 . .
Шаг 3. Обнулим элемент  в матрице в матрице  . Для этого берем . Для этого берем  , , 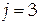 , ,  и строим матрицу и строим матрицу 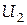 . Имеем . Имеем
 , ,  , ,
 , ,
 . .
Шаг 4. Исходная система преобразована к системе с верхней треугольной матрицей. Пользуясь обратным ходом метода Гаусса, находим  , ,  , ,  . .
ЛЕКЦИЯ № 11
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


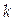 уравнений матрица преобразованной системы имеет вид
уравнений матрица преобразованной системы имеет вид (4.10)
(4.10) из
из  -го уравнения с помощью
-го уравнения с помощью  .
. . Все вычисления в методе оптимального исключения проводятся по формулам
. Все вычисления в методе оптимального исключения проводятся по формулам ,
,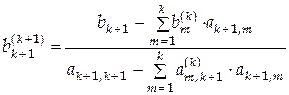
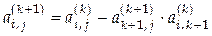 ,
,
 ,
, 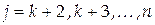 .
. ,
,  .
. -го порядка по методу оптимального исключения необходимо выполнить ровно столько операций умножения и деления, как и в схеме единственного деления Гаусса.
-го порядка по методу оптимального исключения необходимо выполнить ровно столько операций умножения и деления, как и в схеме единственного деления Гаусса. равен нулю. Кроме того, заранее неизвестно, все ли главные миноры матрицы отличны от нуля. В этих случаях обычный метод Гаусса может оказаться непригодным так, как в процессе вычисления какой-то ведущий элемент
равен нулю. Кроме того, заранее неизвестно, все ли главные миноры матрицы отличны от нуля. В этих случаях обычный метод Гаусса может оказаться непригодным так, как в процессе вычисления какой-то ведущий элемент 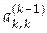 станет равным нулю. Кроме того, если на главной диагонали элемент
станет равным нулю. Кроме того, если на главной диагонали элемент  ,
,  , …,
, …,  ,
,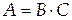 , (4.11)
, (4.11) и
и  - соответственно нижняя и верхняя треугольные матрицы.
- соответственно нижняя и верхняя треугольные матрицы. , с элементами, отличными от нуля, то вместе с равенством
, с элементами, отличными от нуля, то вместе с равенством  . Поэтому диагональные элементы одной из матриц
. Поэтому диагональные элементы одной из матриц  ,
,  (4.12)
(4.12) . Тогда вектор неизвестных
. Тогда вектор неизвестных  можно найти из цепочки матричных уравнений
можно найти из цепочки матричных уравнений ,
,  (4.13)
(4.13) находится из системы с нижней треугольной матрицей
находится из системы с нижней треугольной матрицей
 ,
,  ,
,  . Определив вектор
. Определив вектор 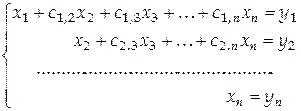
 ,
, 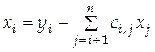 ,
, 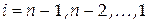 .
. . Среди прямых методов этот метод является самым быстродействующим и особенно удобен для решения систем уравнений с ленточной матрицей, у которой
. Среди прямых методов этот метод является самым быстродействующим и особенно удобен для решения систем уравнений с ленточной матрицей, у которой  при
при  , где
, где 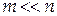 .
. , (4.14)
, (4.14) ,
, .
. ,
,  ,
, ,
,  .
. были положительными числами. Тогда получим
были положительными числами. Тогда получим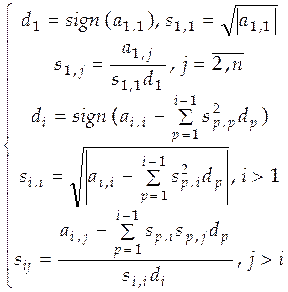 (4.15)
(4.15) ,
,  .
.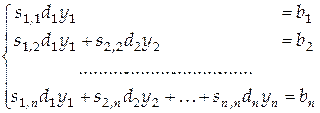
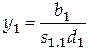 ,
,  ,
, 
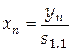 ,
,  ,
,  и
и  . Формулы разложения имеют в этом случае вид
. Формулы разложения имеют в этом случае вид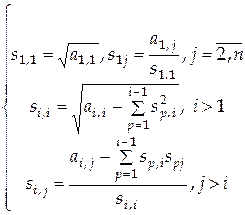
 операций умножения и деления и
операций умножения и деления и  , где
, где  - матрица, сопряженная с
- матрица, сопряженная с  и
и  произвольные вектор-столбцы, причем вектор
произвольные вектор-столбцы, причем вектор  , что построенная по нему матрица отражения
, что построенная по нему матрица отражения  переведет вектор
переведет вектор  .
. , (4.16)
, (4.16) ,
,  ,
,  .
. ,
, 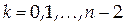
 . Для построения матрицы
. Для построения матрицы  на первом шаге метода в качестве вектора
на первом шаге метода в качестве вектора  . В силу выбора векторов
. В силу выбора векторов  , у которой
, у которой  ,
,  ,
,  . Теперь в качестве
. Теперь в качестве  ,
,  ,
, , у которой все элементы, стоящие ниже главной диагонали, в первых
, у которой все элементы, стоящие ниже главной диагонали, в первых  - шага получим матрицу, первые
- шага получим матрицу, первые  . Система уравнений, соответствующая полученной расширенной матрице, равносильна исходной системе (4.1). Значения неизвестных находятся аналогично обратному ходу метода Гаусса
. Система уравнений, соответствующая полученной расширенной матрице, равносильна исходной системе (4.1). Значения неизвестных находятся аналогично обратному ходу метода Гаусса ,
,  ,
,  операций умножения и деления, а также
операций умножения и деления, а также  извлечений квадратных корней.
извлечений квадратных корней.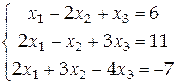
 .
. ,
,  ,
,  ,
,  ,
, ,
,  ,
,  ,
, ,
,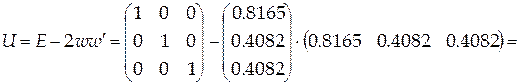
 .
. .
. ,
,  ,
,  ,
,  ,
, ,
,  ,
,  ,
, ,
,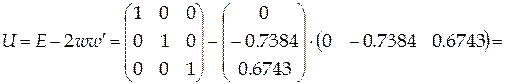
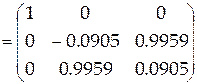 .
. .
. ,
,  ,
,  .
.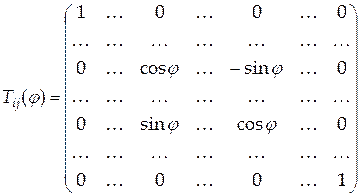
 получим матрицу
получим матрицу  , у которой изменятся в отличие от матрицы
, у которой изменятся в отличие от матрицы  -я и
-я и  -я строки. Изменение элементов
-я строки. Изменение элементов 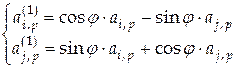 ,
,  . (4.17)
. (4.17) так, чтобы элемент
так, чтобы элемент  оказался равным нулю. Для этого нужно взять
оказался равным нулю. Для этого нужно взять ,
,  , (4.18)
, (4.18) , и
, и  ,
, 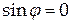 в противном случае.
в противном случае. так, чтобы матрица
так, чтобы матрица  преобразованной системы стала верхней треугольной. Тогда система преобразуется к виду
преобразованной системы стала верхней треугольной. Тогда система преобразуется к виду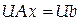 .
. , стоящий под главной диагональю. В этом случае угол поворота выбирается по формулам (4.18).
, стоящий под главной диагональю. В этом случае угол поворота выбирается по формулам (4.18). .
. .
. обнулим элемент
обнулим элемент  . Для этого возьмем
. Для этого возьмем  ,
,  ,
,  и построим матрицу вращений
и построим матрицу вращений  ,
,  ,
, .
. .
.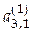 в матрице
в матрице  . Для этого берем
. Для этого берем 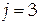 ,
, 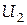 . Имеем
. Имеем ,
,  ,
, ,
, .
. в матрице
в матрице  . Для этого берем
. Для этого берем  ,
,  и строим матрицу
и строим матрицу  ,
,  ,
, ,
, .
. .
.