
|
|
Метод секущих (пропорциональных частей)12 Если первая и вторая производные функции f (x) существуют и сохраняют знак на отрезке [α, β], то метод секущих сходится быстрее, чем метод половинного деления. Чтобы получить формулу метода секущих, заменяют функцию f (x) линейной функцией P(x) = f (α) + определенной на отрезке [α, β]. Функция Р(х) на концах отрезка [α, β] принимает значения f (α) и f (β). В качестве начального приближения корня f (x) берут корень уравнения Р(х) = 0. Его значение определяется х0 = α – Затем рассматривают тот из отрезков [α, х0] и [х0, β], на концах которого функция f (x) принимает значения разных знаков. К выделенному отрезку применяют процесс, описанный выше, и получают следующее приближение корня. Процесс можно оканчивать по выполнению условия | f (xk) | < ε, где ε > 0 – точность окончания итерационного процесса. Пример 2. Методом секущих вычислить корень уравнения (2) на отрезке [0, 1] с точностью 0,01. Проверяем условия применимости метода. f (x) есть полином третьей степени (непрерывна) и f (0) · f (1) < 0. Вычисляем первую и вторую производные функции f (x): f ´(x) = 3x2 + 6x, f ´´(x) = 6x + 6 и убеждаемся, что они сохраняют знак на отрезке [0, 1]. Следовательно, для решения уравнения (2) выгодно применять метод секущих. Последовательно применяя формулу (3), получаем: х1 = x2 = x3 = x4 = x5 = x6 =
 = 0,5311; f (x7) ≈ –0,0039 < 0, | f (x7)| < 0,01. = 0,5311; f (x7) ≈ –0,0039 < 0, | f (x7)| < 0,01.Метод секущих имеет простую геометри- ческую интерпретацию. Функция f (x) = х3 + 3х2 – 1 имеет на отрезке [0, 1] график, показанный на рис.2. На концах отрезка функция при- нимает значения разных знаков. Соединяем точки (0; f (0)), (1; f (1)) прямой и точку пересечения этой прямой с осью Ох прини- маем за первое приближение к корню. В примере х1 = 0,25. Так как и f (0,25) · f (1) < 0, то через точки (0,25; f (0,25)), (1; f (1)) про- водим прямую. Точку пересечения этой пря- мой с осью Ох принимаем за новое прибли- жение к корню. В примере х2 = 0,4074. Этот процесс продолжаем до тех пор, пока не выполнится условие окончания счета. Рис.2.
Решение задачи на ЭВМ В библиотеке программ Mathcad для решения задачи численного решения нелинейных уравнений имеется программа root, в которой реализован метод секущих. Пример работы с такой программой приведен ниже.
Здесь: f(x) – скалярная функция, определяющая уравнение; х – скалярная переменная, относительно которой решается уравнение; 0, 1 – границы интервала, внутри которого происходит поиск корня.
Лабораторная работа рассчитана на ознакомление с методами численного нахождения корней нелинейных уравнений. Для этих целей подходит, например, система программирования PASCAL.
Программы на PASCAL’е Данные программы реализуют методы половинного деления и секущих приближенного вычисления изолированного корня уравнения х3 + 3х2 – 1 = 0 с точностью 0,01. Отрезок, на котором ищется корень, задается в интерактивном режиме. Для нахождения корней других уравнений в описательной части программы вместо левой части уравнения х3 + 3х2 – 1 = 0 следует задать левую часть своего уравнения, а точность вычислений меняется корректировкой константы е. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ( f (β) – f (α) ),
( f (β) – f (α) ), =
=  . (3)
. (3) = 0,25; f (x1) ≈ –0,7969 < 0, | f (x1)| > 0,01.
= 0,25; f (x1) ≈ –0,7969 < 0, | f (x1)| > 0,01.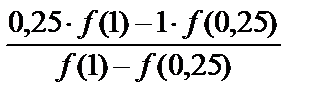 = 0,4074; f (x2) ≈ –0,4344 < 0, | f (x2)| > 0,01.
= 0,4074; f (x2) ≈ –0,4344 < 0, | f (x2)| > 0,01. = 0,4824; f (x3) ≈ –0,1897 < 0, | f (x3)| > 0,01.
= 0,4824; f (x3) ≈ –0,1897 < 0, | f (x3)| > 0,01. = 0,5132; f (x4) ≈ –0,0749 < 0, | f (x4)| > 0,01.
= 0,5132; f (x4) ≈ –0,0749 < 0, | f (x4)| > 0,01. = 0,525; f (x5) ≈ –0,0284 < 0, | f (x5)| > 0,01.
= 0,525; f (x5) ≈ –0,0284 < 0, | f (x5)| > 0,01. = 0,5295; f (x6) ≈ –0,0106 < 0, | f (x6)| > 0,01.
= 0,5295; f (x6) ≈ –0,0106 < 0, | f (x6)| > 0,01.
