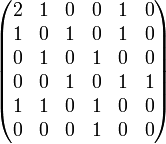Характеристические свойства деревьев

Теорема: для ∀ (p,q) графа G следующие утверждения эквивалентны:
1) Граф G – есть дерево.
2) Любая пара вершин в G соединена единственной цепью.
3) Граф G – связен и q-p+1 = 0
4) Граф G – ацикличен и q-p+1 = 0
5.1) Граф G – ацикличен,
5.2) Если любую пару несмежных вершин G соединить ребром е, то получившийся Граф G+{е} будет иметь в точности один простой цикл.

Следствие 1: Связный (p,q) – граф G есть дерево ⇔ q-p+1 = 0. Доказательство следует из того, что по теореме условия (1) и (3) – эквивалентны.
Следствие 2: Пусть (p,q) – граф G – связен. Тогда G имеет единственный простой цикл ⇔ q-p+1 = 1.
(Необходимость)⇒: Пусть связный (p,q) – граф G удовлетворяет условию q – p + 1=0, следовательно граф G имеет циклическое ребро е. Удалим из G это циклическое ребро е, входящее в некоторый простой цикл С. Получившийся связный граф G’ = G – {e} имеет р вершин и q-1 ребер. Тогда (q-1)-p+1=(q-p+1)-1=0 ⇒ граф G’ есть дерево. Восстановим удаленное ребро е в G’ и получим связный граф G, который имеет единственный простой цикл виде условий 1 и 5 теоремы.
(Достаточность)⇐: пусть теперь связный (p,q) – граф G имеет единственный простой цикл С. Удалим из G его циклическое ребро е, лежащее в С. Полученный связный граф G’ = G – {e}не имеет простых циклов, ибо если G’ имеет простой цикл С’, то G имеет 2 простых цикла C и C’, отличающихся ребром е: цикл С имеет ребро е, а цикл С’ нет. Следовательно, граф G’ есть дерево с тем же числом вершин р. Для дерева G’ число q-1-p+1=0, откуда q-p+1=1

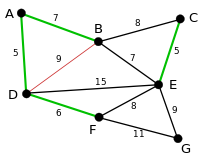
Остовное дерево связного неориентированного графа — ациклический связный подграф данного графа, в который входят все его вершины. Неформально говоря, остовное дерево состоит из некоторого подмножества рёбер графа, таких, что из любой вершины графа можно попасть в любую другую вершину, двигаясь по этим рёбрами, и в нём нет циклов, то есть из любой вершины нельзя попасть в саму себя, не пройдя какое-то ребро дважды.

Число остовных деревьев в полном графе на вершинах выражается формулой Кэли n^n-2

13. Минимальное остовное дерево (или минимальное покрывающее дерево) в связанном, взвешенном, неориентированном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер.

Задача о нахождении минимального остовного дерева часто встречается в подобной постановке: допустим, есть n городов, которые необходимо соединить дорогами, так, чтобы можно было добраться из любого города в любой другой (напрямую или через другие города). Разрешается строить дороги между заданными парами городов и известна стоимость строительства каждой такой дороги. Требуется решить, какие именно дороги нужно строить, чтобы минимизировать общую стоимость строительства.

Эта задача может быть сформулирована в терминах теории графов как задача о нахождении минимального остовного дерева в графе, вершины которого представляют города, рёбра — это пары городов, между которыми можно проложить прямую дорогу, а вес ребра равен стоимости строительства соответствующей дороги.

Алгоритм Крускала (или алгоритм Краскала) — алгоритм построения минимального остовного дерева взвешенного связного неориентированного графа. Алгоритм впервые описан Джозефом Крускалом в 1956 году.

Вначале текущее множество рёбер устанавливается пустым. Затем, пока это возможно, проводится следующая операция: из всех рёбер, добавление которых к уже имеющемуся множеству не вызовет появление в нём цикла, выбирается ребро минимального веса и добавляется к уже имеющемуся множеству. Когда таких рёбер больше нет, алгоритм завершён. Подграф данного графа, содержащий все его вершины и найденное множество рёбер, является его остовным деревом минимального веса.

До начала работы алгоритма необходимо отсортировать рёбра по весу, это требует O(E × log(E)) времени. После чего компоненты связности удобно хранить в виде системы непересекающихся множеств. Все операции в таком случае займут O(E × α(E, V)), где α — функция, обратная к функции Аккермана. Поскольку для любых практических задач α(E, V) < 5, то можно принять её за константу, таким образом общее время работы алгоритма Крускала можно принять за O(E * log(E)).

Алгоритм Крускала действительно находит остовное дерево минимального веса, поскольку он является частным случаем алгоритма Радо — Эдмондса для графического матроида, где независимые множества — ациклические множества рёбер.

Изображение	Описание
	Ребра AD и CE имеют минимальный вес, равный 5. Произвольно выбирается ребро AD (выделено на рисунке).
	Теперь наименьший вес, равный 5, имеет ребро CE. Так добавление CE не образует цикла, то выбираем его в качестве второго ребра.
	Аналогично выбираем ребро DF, вес которого равен 6.
	Следующие ребра — AB и BE с весом 7. Произвольно выбирается ребро AB, выделенное на рисунке. Ребро BD выделено красным, так уже существует путь (зеленый) между B и D, поэтому, если бы это ребро было выбрано, то образовался бы цикл ABD.
	Аналогичным образом выбирается ребро BE, вес которого равен 7. На этом этапе красным выделено гораздо больше ребер: BC, потому что оно создаст цикл BCE, DE, потому что оно создаст цикл DEBA, и FE, потому что оно сформирует цикл FEBAD.
	Алгоритм завершается добавлением ребра EG с весом 9. Минимальное остовное дерево построено.

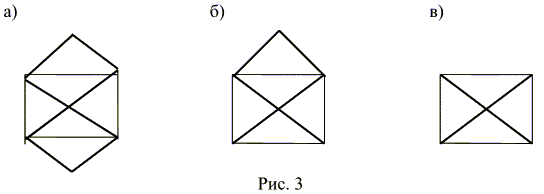
14.Граф (или мультиграф без петель) называется эйлеровым, если существует цикл без повторения ребер (такой цикл называют эйлеровым),обходящий все вершины графа. Граф называется полуэйлеровым,если существует маршрут без повторения ребер (эйлеров путь), обходящий все ребра графа ровно один раз. На рис. 3 изображены: а – эйлеров граф, б – полуэйлеров граф и в – граф, не являющийся ни эйлеровым, ни полуэйлеровым.

Для того чтобы данный связный граф (не орграф, но, возможно, мультиграф без петель) был эйлеровым, необходимо и достаточно, чтобы степени всех вершин были четными. Данный связный граф будет полуэйлеровым тогда и только тогда, когда степени двух вершин будут нечетными, а степени остальных вершин – четными.

15.Пусть G – эйлеров граф, тогда следующая процедура всегда возможна и приводит к эйлеровой цепи графа G. Выходя из произвольной вершины и, идём по рёбрам графа произвольным образом, соблюдая лишь следующие правила:

1) стираем рёбра по мере их прохождения и стираем также изолированные вершины, которые при этом образуются;

2) на каждом этапе идём по мосту только тогда, когда нет других возможностей.

Доказательство: Покажем сначала, что указанная процедура может быть выполнена на каждом этапе. Предположим, что мы достигли некоторой вершины V; тогда если V¹U, то оставшийся подграф H связен и содержит ровно две вершины нечётной степени, а именно U и V. Согласно теореме 3 и определению полуэйлерова графа, граф H содержит полуэйлерову цепь P из V в U. Поскольку удаление первого ребра цепи Р не нарушает связности графа Н, то описанное в теореме построение (Т 1б)) возможно на каждом этапе. Если же V=U, то доказательство остаётся тем же самым до тех пор, пока есть ещё рёбра, инцидентные вершине U.

Осталось только показать, что данная процедура всегда приводит к полной эйлеровой цепи. Но это очевидно, так как в G не может быть рёбер, оставшихся не пройденными после использования последнего ребра, инцидентного U. В противном случае удаление некоторого ребра, смежного одному из оставшихся, привело бы к несвязному графу, что противоречит условию 2)

16.Гамильтоновы и полугамильтоновы графы.

17. Матрица смежности — один из способов представления графа в виде матрицы.

Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента a_ij равно числу рёбер из i-й вершины графа в j-ю вершину.

Иногда, особенно в случае неориентированного графа, петля (ребро из i-й вершины в саму себя) считается за два ребра, то есть значение диагонального элемента a_ii в этом случае равно удвоенному числу петель вокруг i-й вершины.

Матрица смежности простого графа (не содержащего петель и кратных ребер) является бинарной матрицей и содержит нули на главной диагонали.

Ниже приведён пример неориентированного графа и соответствующей ему матрицы смежности A. Этот граф содержит петлю вокруг вершины 1, так что, в зависимости от конкретных приложений, элемент a₁₁ может считаться равным либо единице (как показано ниже), либо 0.

Граф	Матрица смежности

· a_ij - число ребер, связывающих вершины v_i и v_j, причем при i=j каждая петля учитывается дважды.

· Матрица смежности пустого графа, не содержащего ни одного ребра, состоит из одних нулей.

Матрица инцидентности — одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро(дуга) и вершина). Столбцы матрицы соответствуют ребрам, строки — вершинам. Ненулевое значение в ячейке матрицы указывает связь между вершиной и ребром (их инцидентность).

В случае ориентированного графа каждому ребру <x,y> ставится в соответствие "-1" на позиции (x,y) и "1" на позиции (y,x); если связи между вершинами нет, то ставится в соответствие "0".

Не нашли, что искали? Воспользуйтесь поиском по сайту: