
|
|
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ12
1.Скалярным произведением векторов Скалярное произведение векторов
Свойства скалярного произведения двух векторов.
1. 2. 3. 4. 5. 6. 7. 8. если 9. если Так как направление нуль-вектора произвольно, то девятое свойство можно переформулировать как необходимое и достаточное условие ортогональности векторов: два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю. Из определения скалярного произведения и свойств косинуса непосредственно вытекает неравенство Коши-Буняковского. Для любых векторов
При этом, если 3. Механический смысл скалярного произведения заключается в следующем: если материальная точка под воздействием силы
4. Из свойств скалярного произведения вытекает, что линейные комбинации векторов можно перемножать как многочлены. Возьмем в пространстве векторов базис
Здесь
Матрица Гназывается матрицей Грамаскалярного произведения для базиса е. Используя матрицу Грама, можно получить формулу для вычисления Свойства матрицы Грама. 10. Матрица Грама симметрична относительно главной диагонали. 20.Диагональные элементы матрицы Грама строго положительны. 30. Для матрицы Грама и любого n-мерногостолбца х выполняется условие х Т×Г×х > 0. Равенства
Позволяют по координатам векторов и метрическим коэффициентам базиса находить длины векторов и углы между ними. Базис е = (е1, е2, ... , еn ) (на прямой, на плоскости или в пространстве называется ортонормированным, если
Длины векторов ортонормированного базиса равны единице:
Матрица Грама для ортонормированного базиса имеет вид
Ортонормированный базис в пространстве V2 обычно обозначается 5. Пусть в ортонормированном базисе
В ортонормированном базисе скалярное произведение двух векторов равно сумме попарных произведений их соответствующих координат.
Вычисление длины вектора в ортонормированном базисе.
Вычисление угла между векторами в ортонормированном базисе
Вычисление координат орта вектора в ортонормированном базисе
Вычисление ортогональной проекции вектора на направление в ортонормированном базисе
Замечание.Если Косинусы углов, которые отличный от нуля вектор образует с векторами ортонормированного базиса, называются направляющими косинусами.
Направляющие косинусы удовлетворяют соотношению
Из полученных выражений для направляющих косинусов видно, что они совпадают с координатами орта вектора.
Если A(x1, y1, z1), B(x2, y2, z2), то (x2 – x1, y2 – y1, z2 – z1) , то ½½= . Обозначим r(A, B) – расстояние между точками A и B. Тогда r(A, B) вычисляется по той же формуле. Отметим, что эта функция обладает следующими свойствами: 1. r(A, B) = r(B, A); 2. r(A, B) + r(B, C) ³ r(A, C) (неравенство треугольника); 3. r(A, B) ³ 0, и r(A, B) = 0 Û A = B.
6. Если задан некоторый вектор Аналогично,ортогональной составляющейвектора 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и
и  называется действительное число, равное произведению длин векторов на косинус угла между ними.
называется действительное число, равное произведению длин векторов на косинус угла между ними. или
или  . Итак,
. Итак, .
.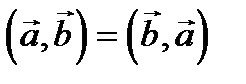 (коммутативность);
(коммутативность); (скалярный квадрат вектора равен квадрату его длины);
(скалярный квадрат вектора равен квадрату его длины); ;
;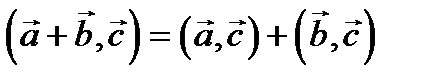 (линейность);
(линейность); (линейность);
(линейность); ;
; (положительная определенность).
(положительная определенность). , то
, то  ;
; .
. 0, то
0, то  тогда и только тогда, когда
тогда и только тогда, когда  , где
, где  .
. перемещается на вектор
перемещается на вектор  , то совершаемая этой силой работа равна скалярному произведению
, то совершаемая этой силой работа равна скалярному произведению  .
. . Тогда для векторов
. Тогда для векторов  и
и 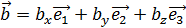 имеем
имеем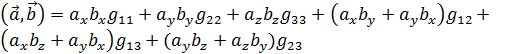 .
. - метрические коэффициенты. Составим из метрических коэффициентов матрицу
- метрические коэффициенты. Составим из метрических коэффициентов матрицу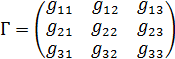
 .
. и
и 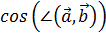 =
= 


 .
. , в пространстве V3 -
, в пространстве V3 -  .
. ,
,  .
.
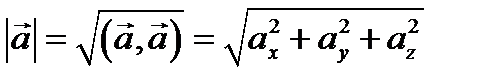
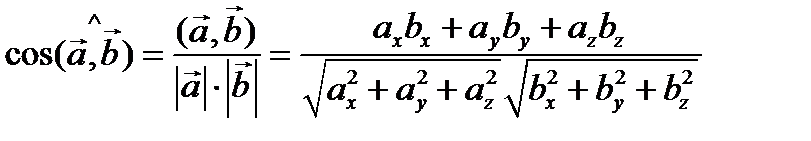 , откуда:
, откуда: .
.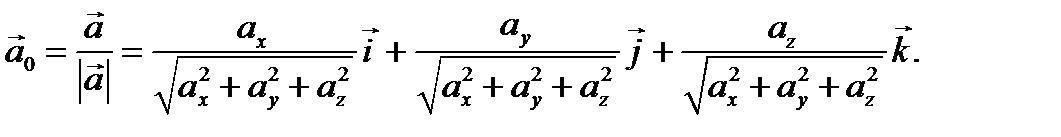
 .
.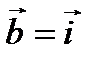 , то
, то  . Аналогично,
. Аналогично,  . Таким образом, координаты вектора в ортонормированном базисе являются его ортогональными проекциями на направления, заданные соответствующими ортами.
. Таким образом, координаты вектора в ортонормированном базисе являются его ортогональными проекциями на направления, заданные соответствующими ортами.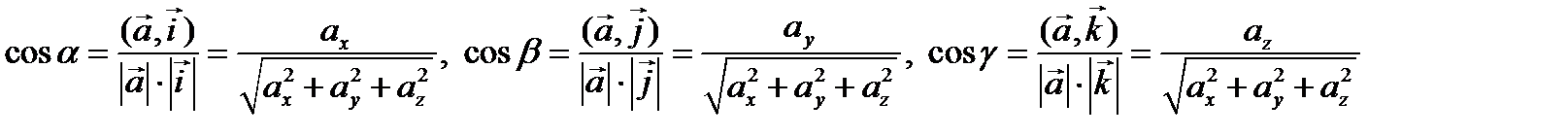 .
. .
. .
. , то ортогональной составляющей произвольного вектора
, то ортогональной составляющей произвольного вектора  вдоль вектора
вдоль вектора  , который коллинеарен
, который коллинеарен 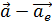 перпендикулярна вектору
перпендикулярна вектору  называется вектор
называется вектор  , компланарный плоскости
, компланарный плоскости  , причем разность
, причем разность  перпендикулярна этой плоскости.
перпендикулярна этой плоскости.