
|
|
Расчёт абсолютной, относительной и приведенной погрешностей результатов измерений12 Содержание
Задание и исходные данные
Используя ряд многократных измерений линейного размера (L) элемента конструкции химического оборудования, приведенный в нижеприведенной таблице задания, умноженных на порядковый номер студента в журнале учебной группы, выполнить: 1) расчёт абсолютной, относительной и приведенной погрешностей результатов измерений; 2) выделение аддитивной и мультипликативной составляющих из абсолютной и относительной погрешностей результатов измерений, построить их графические зависимости; 3) необходимые вычисления по определению факта наличия или отсутствия систематических погрешностей в исходном ряду измерений линейного размера элемента конструкции, используя метод последовательных разностей и метод дисперсионного анализа; 4) необходимые вычисления по выявлению грубых погрешностей в исходном ряду измерений линейного размера элемента конструкции, используя критерии: Граббса, «трёх сигм», Шарлье, Шовене, Диксона.
Таблица №1 Результаты измерений линейного размера L (в сантиметрах)
Все приведенные результаты измерений проводились одним и тем же средством измерений, в одних и тех же внешних условиях, одним и тем же субъектом измерения, с одинаковой тщательностью. При проведении всех расчётов за истинное (действительное) значение линейного размера (L) принять значение равное 1.1 см, умноженному на порядковый номер студента в журнале учебной группы. Порядковый номер студента ____13_____ в журнале учебной группы ЗТСБсд-114. Расчёт абсолютной, относительной и приведенной погрешностей результатов измерений Определение «погрешность» является одним из центральных в метрологии, в котором используются понятия «погрешность результата измерения» и «погрешность средства измерения». Погрешностью измерения называется отклонение результата измерения от истинного значения измеряемой физической величины. Так как истинное значение измеряемой величины неизвестно, то при количественной оценке погрешности пользуются действительным значением физической величины. Это значение находится экспериментальным путем и настолько близко к истинному значению, что для поставленной измерительной задачи может быть использовано вместо него. Погрешность средства измерения − разность между показаниями СИ и истинным (действительным) значением измеряемой физической величины. Она характеризует точность результатов измерений, проводимых данным средством. По способу количественного выражения погрешности измерения делятся на абсолютные, относительные и приведенные. Абсолютной погрешностью ∆, выражаемой в единицах измеряемой величины, называется отклонение результата измерения «X» от истинного значения «Xи»:
Абсолютная погрешность характеризует величину и знак полученной погрешности, но не определяет качество самого проведенного измерения. Относительной погрешностью δ называется отношение абсолютной погрешности измерения к истинному значению измеряемой величины:
Погрешность δ часто выражают в процентах:
Приведенной погрешностью δпр, выражающей потенциальную точность измерений, называется отношение абсолютной погрешности ∆, к некоторому нормирующему значению XN (например, к конечному значению шкалы прибора или сумме конечных значений шкал при двухсторонней шкале):
Представим результаты измерений линейного размера L (в сантиметрах) элемента конструкции (таблица №1 задания) с учетом порядкового номера «13» студента, в виде:
Таблица №2.1 Результаты измерений линейного размера L (в сантиметрах) элемента химического оборудования с учётом порядкового номера студента
Истинное (действительное) значение линейного размера (L) элемента конструкции с учётом задания составит 14,3 см. Тогда, применяя выражение (2.1), рассчитаем суммарные (т.е. содержащие аддитивные и мультипликативные составляющие) абсолютные погрешности (Δсi) для каждого измерения:
Результаты расчётов суммарных абсолютных погрешностей приведены в таблице 2.2.
Таблица №2.2 Суммарные абсолютные погрешности
Применяя полученные значения суммарной абсолютной погрешности (Δсi), рассчитаем среднее значение абсолютной погрешности Δср по зависимости вида:
Подставив в формулу (2.4) необходимые данные из таблицы 2.2, получим
Таблица 2.3 Суммарные относительные погрешности
Применяя полученные значения суммарной относительной погрешности (δ сi), рассчитаем среднее значение абсолютной погрешности (δ ср) по зависимости вида:
Подставив в формулу (2.5) необходимые данные из таблицы 2.3, получим 0,127, что в процентах соответствует 12,7%. Для расчёта приведенной погрешности результатов измерений, в соответствии с формулой (2.3), необходимо знание нормирующего значения XN, которое, в соответствии с заданием, не определено. Поэтому, учитывая реальные линейные размеры элемента конструкции строящегося здания, допустим, что средство измерения этих размеров имеет конечное значение шкалы, например, 25 см. Тогда средняя приведенная погрешность, с учётом выше рассчитанного значения Δср 1,82 см, составит:

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (2.1)
(2.1)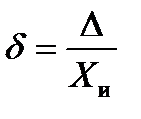 (2.2)
(2.2)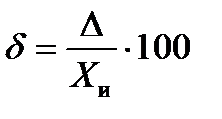 [%].
[%]. [%]. (2.3)
[%]. (2.3)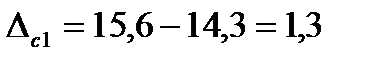 ;
; ;
; …
…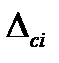 , см
, см
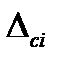 , см
, см
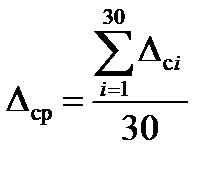 (2.4)
(2.4)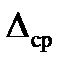 1,82 см. Используя рассчитанные значения суммарной абсолютной погрешности (Δсi), рассчитываются суммарные относительные погрешности измерений (δсi), применяя зависимость вида (2.2):
1,82 см. Используя рассчитанные значения суммарной абсолютной погрешности (Δсi), рассчитываются суммарные относительные погрешности измерений (δсi), применяя зависимость вида (2.2):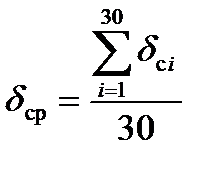 (2.5)
(2.5)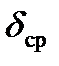
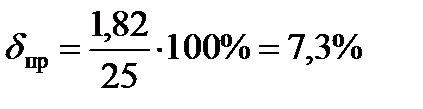 .
.