
|
|
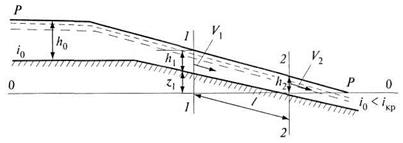
СВОБОДНОЙ ПОВЕРХНОСТИ СПОСОБОМ В. ЧАРНОМСКОГОЭтот способ удобен тем, что для расчета изменения глубины вдоль открытого потока не требуется применения специальных таблиц. Способ может использоваться как для непризматических, так и для призматических русел. Для вывода способа В. Чарномского рассмотрим неравномерный поток, представленный на рис. 8.11.
Рис. 8.11. К выводу уравнения В. Чарномского Составим уравнение Бернулли для сечений 1-1 и 2-2 относительно горизонтальной плоскости сравнения, проходящей на уровне наинизшей точки сечения 2-2. В сечении 1-1 глубина потока
При уклоне дна
Величины
Гидравлические потери по длине
Уравнение (8.33) примет следующий вид после соответствующих подстановок:
Удельная энергия потока в сечении 1-1
В сечении 2-2
Тогда согласно (8.35) получим
Разность удельных энергий в сечениях потока
Считаем с некоторой степенью приближения, что гидравлические потери по длине при неравномерном движении соответствуют потерям для равномерного движения. Следовательно, гидравлический уклон можно определить по формуле Шези:
Однако при определении Средняя скорость потока между этими сечениями
Среднее значение коэффициента Шези
Средний гидравлический радиус
Средний гидравлический уклон
Окончательно получим следующее выражение для длины между выбранными сечениями:
В связи с осреднением гидравлического уклона и заменой дифференциального уравнения уравнением в конечных разностях расстояние между сечениями по уравнению (8.44) получается достаточно приближенным. Для получения большей точности при расчете кривой свободной поверхности следует расстояние поделить на несколько большее количество участков. Чем меньше принимается расстояние между участками, тем выше получается точность расчетов. Порядок расчетов следующий: · устанавливается форма кривой свободной поверхности потока; · назначается исходное сечение: например, для кривой спада - сечение с критической глубиной; для кривой подпора - сечение с нормальной глубиной; · кривая свободной поверхности разбивается на n участков; · определяются удельные энергии сечений в начале и конце каждого участка; · определяются гидравлические уклоны в начале и конце каждого участка, а также среднее значение гидравлического уклона на всей длине участка; · производится расчет длины каждого участка. Способ, предложенный В. Чарномским, может быть применен для русла любого поперечного сечения. В случае призматического русла решение уравнения (8.44) по определению глубины в нем существенно упрощается. Известны другие методы интегрирования дифференциального уравнения неравномерного движения - способы Н. Павловского, К. Михайлова, В. Даденкова и др. ♦ Пример 8.2 В конце трапецеидального водоотводного канала установлена плотина, создавшая подпор в канале (см. рис. 8.1). В результате этого движение воды в канале стало неравномерным установившимся. Уклон дна канала Отрезки длин кривой свободной поверхности определяем по формуле (8.44):
Первый отрезок: Смоченные периметры: Площади сечений: Гидравлический радиус: Коэффициенты Шези: Удельные энергии сечений при глубинах
Средняя скорость
Средний коэффициент Шези
Средний гидравлический радиус
Длина отрезка
Результаты вычислений для других отрезков сведены в табл. 8.2 и 8.3. Таблица 8.2 - Результаты вычислений
Таблица 8.3 - Результаты вычислений
На рис. 8.12 приведена схема построения кривой свободной поверхности.
Рис. 8.12. Кривая свободной поверхности в канале
ГИДРАВЛИЧЕСКИЙ ПРЫЖОК При проведении анализа изменения глубины по длине неравномерного установившегося потока было отмечено, что для русел с любым уклоном дна кривая свободной поверхности пересекает линию критических глубин практически под прямым углом, и в случае образования кривой подпора возникает гидравлический прыжок. Гидравлический прыжок - явление резкого увеличения глубины при переходе потока из бурного состояния в спокойное, когда глубина изменяется от В системах водоотведения гидравлический прыжок образуется на очистных сооружениях при истечении потоков из-под щита и в перепадных колодцах, при изменении уклона трассы коллектора и в других случаях. На транспортных магистралях гидравлический прыжок может иметь место в водопропускных и водоотводных сооружениях (каналы, трубы, малые мосты, перепады, быстротоки). Прыжок, в котором над основанием транзитного потока образуется валец с водоворотным движением, называется совершенным гидравлическим прыжком. Рассмотрим гидравлический прыжок на примере истечения жидкости из-под щита (рис. 8.13). Гидравлический прыжок можно разделить на две характерные зоны - транзитная струя и валец (водоворот), находящийся над транзитной струей.
Рис. 8.13. Совершенный гидравлический прыжок При истечении из-под щита потенциальная энергия жидкости перед щитом переходит в кинетическую энергию вытекающей струи. За счет большой скорости истечения сразу за щитом поток в начале прыжка находится в бурном состоянии и глубина его В результате образования прыжка наблюдается поверхность раздела между транзитной струей и вальцем, представленная на рис. 8.13 линией ABC. После точки А транзитный поток расширяется от глубины Разность отметок свободной поверхности потока до прыжка и после него В вальце происходит вращательное движение жидкости, при этом он насыщен пузырьками воздуха. Верхняя поверхность вальца имеет волнообразную форму. В нижней части вальца, от начала к концу прыжка, движение совпадает с направлением транзитной струи; в верхней части вальца движение происходит против основного направления потока, от конца прыжка к его началу. На некоторой глубине из-за вращательного движения жидкости внутри вальца скорость В транзитной струе, расположенной под вальцем, происходит движение жидкости. Гидравлический прыжок можно рассматривать как затопленную полуограниченную струю, вытекающую из отверстия в однородную жидкость. Такой подход к рассмотрению прыжка позволяет несколько лучше представить физическую модель прыжка, в которой транзитный растекающийся поток является основным участком струи. В зоне поверхности раздела между вальцами и транзитным потоком, за счет пульсации скоростей и давления происходит интенсивный массобмен частичками жидкости. За гидравлическим прыжком осуществляется выравнивание эпюры скоростей, и окончательно эпюра скорости приобретает форму, соответствующую равномерному установившемуся движению потока в открытом русле. Участок от прыжка до сечения, в котором эпюра скорости выравнивается, называется послепрыжковым, а длина этого участка обозначается Следует отметить, что на участке вальца за счет вихреобразования имеют место наибольшие скорости у дна русла и они уменьшаются на послепрыжковом участке. Рассмотрим совершенный гидравлический прыжок (рис. 8.13), считая длину прыжка достаточно малой и уклон дна русла Рассмотрим два сечения - 1-1 в начале прыжка и 2-2 в его конце - и проведем координатную ось х по дну русла. Для вывода уравнения прыжка используем теорему об изменении количества движения применительно к объему жидкости AbdC массой m, заключенному между сечениями 1-1 и 2-2. Предположим, что за короткий промежуток времени dt сечение потока 1-1 переместится в положение 1'-1', а сечение 2-2 за тот же промежуток времени - в положение 2'-2' соответственно на длины Изменение проекции количества движения на ось х за время dt равно разности количества движения массы объемов A'b'd'C' и AbdC. Следовательно, изменение количества движения
Массе жидкости, проходящей через сечение 2-2, соответствует масса объема dCC'd' и равняется массе жидкости объема Abb'А' первого сечения. Масса
Изменение количества движения
где Средние скорости в сечениях с площадями живого сечения
Изменения количества движения за время dt
Определим сумму проекций на ось х импульсов сил, действующих на объем жидкости AbdC, за тот же промежуток времени. Для этого принимаем следующие допущения: • считаем, что в сечениях 2-2 и 1-1 движение плавно изменяющееся; • в виду достаточно малой длины прыжка пренебрегаем силами трения потока жидкости в прыжке о стенки русла. В связи с принятыми допущениями при определении импульса сил учитываются только силы давления жидкости в сечениях 1-1 - Для плавно изменяющегося движения гидростатический напор в любой точке взятого сечения постоянен, т.е. соблюдается распределение давления по гидростатическому закону. Поэтому силы давления
где
Изменение количества движения равно импульсу сил:
После некоторых упрощений и перестановок в (8.50) получим основное уравнение гидравлического прыжка
При заданном расходе левая часть уравнения (8.51) является функцией глубины
Функция
где Используя свойство, что прыжковые функции равны, можно найти одну из глубин, если другая известна. Решение этой функции показывает, что при критической глубине она имеет минимальное значение. На рис. 8.14 изображен график прыжковой функции, построенной согласно зависимости (8.52).
Рис. 8.14. График прыжковой функции На рис. 8.14 приведена кривая удельной энергии сечения График этой функции Исследование графика прыжковой функции позволяет сделать следующие выводы: · глубины в начале · изменение глубины в начале прыжка ведет к изменению глубины в его конце, причем эта зависимость обратная. Увеличение глубины Построив график прыжковой функции для данного русла, при заданном расходе Q можно, зная одну из глубин - 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и скорость
и скорость  , а в сечении 2-2 соответственно
, а в сечении 2-2 соответственно  и
и 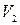
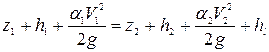 . (8.33)
. (8.33) понижение отметки дна русла на участке 1-1 и 2-2 длиной
понижение отметки дна русла на участке 1-1 и 2-2 длиной 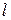
 .
.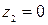 ,
, 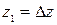 ;
; . (8.34)
. (8.34)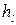 на выбранном участке выразим через гидравлический уклон
на выбранном участке выразим через гидравлический уклон  :
: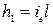 .
. . (8.35)
. (8.35) . (8.36)
. (8.36)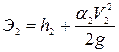 . (8.37)
. (8.37)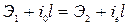 . (8.38)
. (8.38) . (8.39)
. (8.39)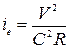 .
.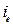 принимаем его среднее значение относительно сечений 1-1 и 2-2.
принимаем его среднее значение относительно сечений 1-1 и 2-2.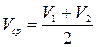 . (8.40)
. (8.40) . (8.41)
. (8.41)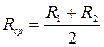 . (8.42)
. (8.42)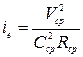 . (8.43)
. (8.43) . (8.44)
. (8.44) ; ширина канала
; ширина канала  м; заложение откосов
м; заложение откосов  ; расход воды в канале
; расход воды в канале 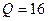 м3/с. Глубина воды перед плотиной
м3/с. Глубина воды перед плотиной 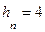 м. Построить кривую свободной поверхности. Нормальная глубина в канале
м. Построить кривую свободной поверхности. Нормальная глубина в канале 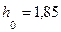 м.
м. .
.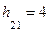 м;
м; 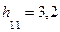 м.
м. м;
м;  м.
м.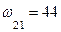 м2;
м2; 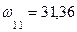 м2.
м2. м;
м;  м.
м.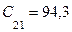 мl/2/c;
мl/2/c;  мl/2/c.
мl/2/c.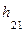 и
и  ,
,  :
: м;
м;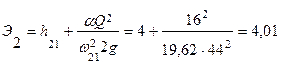 м.
м. м/с.
м/с.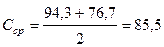 мl/2/c
мl/2/c м.
м. м.
м.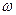 , м2
, м2
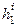 , м
, м
 , м
, м
 , м/с
, м/с
 , м1/2/с
, м1/2/с
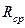 , м
, м
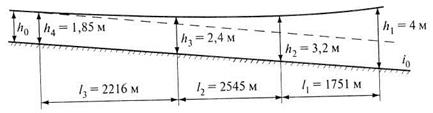
 до
до 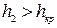 . Гидравлический прыжок может происходить в результате движения жидкости через плотины, входящие в состав гидроузлов водохранилищ. Гидравлический прыжок образуется, когда поток из бурного состояния в результате перелива через плотину переходит в спокойное состояние.
. Гидравлический прыжок может происходить в результате движения жидкости через плотины, входящие в состав гидроузлов водохранилищ. Гидравлический прыжок образуется, когда поток из бурного состояния в результате перелива через плотину переходит в спокойное состояние.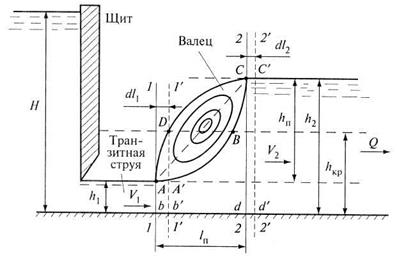
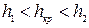 .
. называется высотой прыжка. Расстояние между началом и концом прыжка - длина прыжка
называется высотой прыжка. Расстояние между началом и концом прыжка - длина прыжка  .
. . Положение прыжка несколько изменяется во времени - он смещается влево и вправо от рассматриваемого положения.
. Положение прыжка несколько изменяется во времени - он смещается влево и вправо от рассматриваемого положения.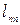 .
. . Сечение русла на участке прыжка постоянно и может иметь любую форму. Расход жидкости равен Q.
. Сечение русла на участке прыжка постоянно и может иметь любую форму. Расход жидкости равен Q.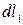 и
и  . При этом объем жидкости AbdC, заключенный между сечениями 1-1 и 2'-2', займет положение объема потока жидкости A'b'd'C'.
. При этом объем жидкости AbdC, заключенный между сечениями 1-1 и 2'-2', займет положение объема потока жидкости A'b'd'C'.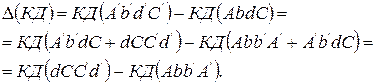 . (8.45)
. (8.45) .
. , (8.46)
, (8.46) и
и  - средние скорости в сечениях 2-2 и 1-1.
- средние скорости в сечениях 2-2 и 1-1. и
и 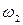
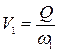 и
и 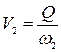 .
.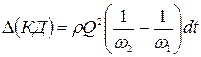 . (8.47)
. (8.47) и 2-2 -
и 2-2 - 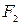 , проекция силы тяжести на ось х равна нулю.
, проекция силы тяжести на ось х равна нулю.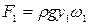 ;
; 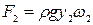 , (8.48)
, (8.48)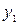 , и
, и 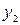 - погружение центров тяжести сечений соответственно площадей
- погружение центров тяжести сечений соответственно площадей  , и
, и 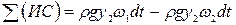 . (8.49)
. (8.49) . (8.50)
. (8.50) . (8.51)
. (8.51) , так же как и правая часть уравнения. Для любого сечения в пределах гидравлического прыжка можно записать
, так же как и правая часть уравнения. Для любого сечения в пределах гидравлического прыжка можно записать . (8.52)
. (8.52) , (8.53)
, (8.53) и
и 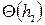 - функции, соответствующие глубинам в русле
- функции, соответствующие глубинам в русле 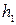 , и
, и 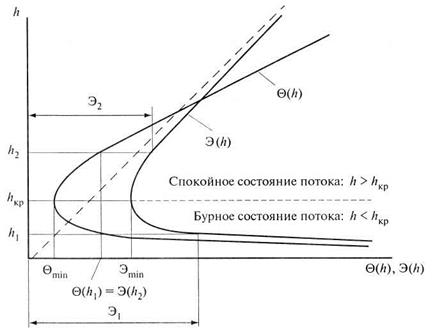
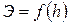 .
. , чем функции
, чем функции  .
.