|
Расстояние от точки до плоскости
Дано:  , П : Ах + Ву + Сz + D = 0, М(х0, у0, z0).
Найти расстояние d(M0, П) от точки М0 до плоскости П.
Из уравнения плоскости П следует, что вектор , П : Ах + Ву + Сz + D = 0, М(х0, у0, z0).
Найти расстояние d(M0, П) от точки М0 до плоскости П.
Из уравнения плоскости П следует, что вектор 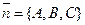 перпендикулярен плоскости П. Опустим из точки М0 перпендикуляр NM0 на плоскость П (рис. 51). Пусть N(x1, y1, z1). Тогда Ax1 + By1 + Cz1 + D = 0 (*). Искомое расстояние
d(M0, П) = перпендикулярен плоскости П. Опустим из точки М0 перпендикуляр NM0 на плоскость П (рис. 51). Пусть N(x1, y1, z1). Тогда Ax1 + By1 + Cz1 + D = 0 (*). Искомое расстояние
d(M0, П) = 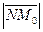 (**) (**)
| 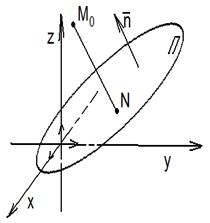 Рис. 51
Рис. 51
| Вектор 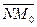 коллинеарен с вектором коллинеарен с вектором 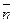 . Так как . Так как 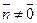 , то , то 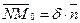 (***). Отсюда и из равенства (**) следует, что d(M0, П) = (***). Отсюда и из равенства (**) следует, что d(M0, П) = 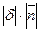 = = 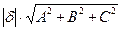 (****). Итак, задача свелась к нахождению d. Умножим скалярно на (****). Итак, задача свелась к нахождению d. Умножим скалярно на 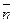 обе части равенства (***), получим обе части равенства (***), получим 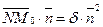 . Перейдя к координатам и учитывая, что система координат прямоугольная, получим . Перейдя к координатам и учитывая, что система координат прямоугольная, получим
A(x0 - x1) + B(y0 - y1) + C(z0 - z1) = d(A2 + B2 + C2).
Так как A2 + B2 + C2 ¹ 0, то 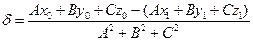 . Из равенства (*) следует, что . Из равенства (*) следует, что 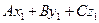 = -D. Итак, = -D. Итак,  . Подставив d в (**), получим . Подставив d в (**), получим
d(M0, П) = 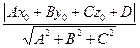 (52) (52)
Задача 18. Дано:  , П : 12х + 3у - 4z - 35 = 0. , П : 12х + 3у - 4z - 35 = 0.
Найдите уравнения плоскостей, параллельных П и отстоящих от неё на расстоянии 5.
Решение. Обозначим искомые плоскости П1 и П2 . Тогда М Î (П1 È П2) Û d(M, П) = 5. Используя формулу (52), получим М Î (П1 È П2) Û  . После упрощения получим . После упрощения получим 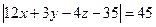 . Раскрывая модуль, получим уравнения двух плоскостей: . Раскрывая модуль, получим уравнения двух плоскостей:
П1 : 12х + 3у - 4z - 80 = 0 и П2 : 12х + 3у - 4z + 10 = 0.
Расстояние от точки до прямой
Дано:  , l : , l : 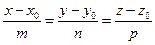 , М1(x1, y1, z1).
Найти расстояние d (M1, l).
Из уравнений прямой l следует, что точка M0 (x0, y0, z0 ) лежит на прямой l и вектор , М1(x1, y1, z1).
Найти расстояние d (M1, l).
Из уравнений прямой l следует, что точка M0 (x0, y0, z0 ) лежит на прямой l и вектор 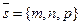 параллелен этой прямой. Искомое расстояние равно высоте параллелограмма, параллелен этой прямой. Искомое расстояние равно высоте параллелограмма,
| 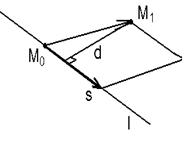 Рис. 52
Рис. 52
| построенного на векторах 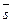 и и 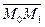 как на сторонах (рис. 52). как на сторонах (рис. 52).
Следовательно,
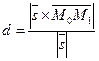 . .
Переписав это равенство в координатах, получим
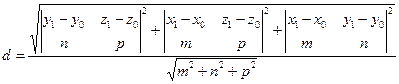 (53) (53)
Расстояние между скрещивающимися прямыми
Дано:  , l1: , l1: 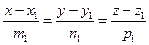 , l2 : , l2 : 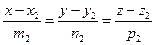 , l1 и l2 скрещиваются.
Найти d (l1, l2).
Из уравнений l1 и l2 следует, что M1 (x1, y1, z1) Î l1, M2 (x2, y2, z2)Î l2 и векторы , l1 и l2 скрещиваются.
Найти d (l1, l2).
Из уравнений l1 и l2 следует, что M1 (x1, y1, z1) Î l1, M2 (x2, y2, z2)Î l2 и векторы 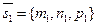 и и  параллельны параллельны
| 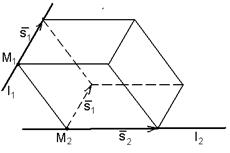 Рис. 53
Рис. 53
| прямым l1 и l2 соответственно. Искомое расстояние равно высоте параллелепипеда, построенного на векторах 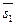 , , 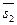 и и 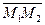 . Следовательно, . Следовательно,
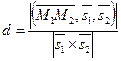 . .
Переписав это равенство в координатах, получим
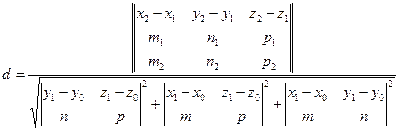 (54) (54)
Задача 19. Дано:  , l1 : , l1 : 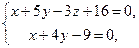 l2 : l2 : 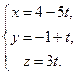
Проверьте, что l1 и l2 скрещиваются и найдите расстояние между ними.
Решение. Найдём направляющий вектор прямой l1 и какую-нибудь точку на ней.
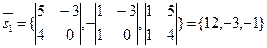 , М1 = {1, 2, 9}. Из уравнений l2 следует, что М2 (4, -1, 0) и , М1 = {1, 2, 9}. Из уравнений l2 следует, что М2 (4, -1, 0) и 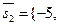 1, 3}. 1, 3}.
Вычислим 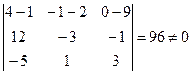 . Следовательно, l1 и l скрещиваются. Найдём . Следовательно, l1 и l скрещиваются. Найдём 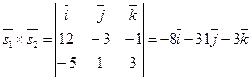 . Следовательно, . Следовательно,
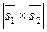 = = 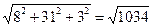 и и 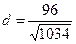 . .
3.6.3. Геометрический смысл неравенства Ах + Ву + Сz + D ³ 0 (£ 0, > 0, < 0)
Дано:R = 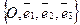 , Ах + Ву + Сz + D ³ 0.
Исследовать, какую фигуру задаёт данное неравенство.
Уравнение Ах + Ву + Сz + D = 0 задаёт плоскость. Пусть это плоскость П. Рассмотрим все точки пространства, не лежащие на П.
Вектор , Ах + Ву + Сz + D ³ 0.
Исследовать, какую фигуру задаёт данное неравенство.
Уравнение Ах + Ву + Сz + D = 0 задаёт плоскость. Пусть это плоскость П. Рассмотрим все точки пространства, не лежащие на П.
Вектор 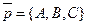 не параллелен плоскости П. Действительно, если бы не параллелен плоскости П. Действительно, если бы 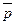 был параллелен П, то А×А + В×В + С×С = А2 + В2 + С2= 0. Но это невозможно. был параллелен П, то А×А + В×В + С×С = А2 + В2 + С2= 0. Но это невозможно.
| 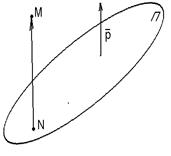 Рис. 54
Рис. 54
| Рассмотрим множество всех точек пространства, не лежащих на плоскости П. Пусть М – любая из этих точек. Проведём через точку М прямую, параллельную вектору 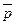 , и пусть она пересекает П в точке N. Векторы , и пусть она пересекает П в точке N. Векторы 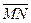 и и 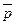 коллинеарны, коллинеарны, 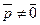 , следовательно, , следовательно, 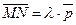 . (*) Очевидно, l > 0 Û когда точки М лежат в одной открытой полуплоскости с границей П, а именно в той, в сторону которой направлен вектор . (*) Очевидно, l > 0 Û когда точки М лежат в одной открытой полуплоскости с границей П, а именно в той, в сторону которой направлен вектор 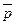 . И l < 0 Û когда точки М лежат в другой открытой полуплоскости с этой же границей. Перейдём к координатам. Пусть М (х, у, z) и N (х1, у1, z1). Тогда . И l < 0 Û когда точки М лежат в другой открытой полуплоскости с этой же границей. Перейдём к координатам. Пусть М (х, у, z) и N (х1, у1, z1). Тогда 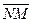 = {x - x1, y - y1, z - z1}. Равенство (*) в координатах перепишется: = {x - x1, y - y1, z - z1}. Равенство (*) в координатах перепишется:
x - x1 = lA, y - y1 = lB, z - z1 = lC.
Отсюда x1 = x - lA, y1 = y - lB, z1 = z - lC. Так как N Î П, то Ах1 + Ву1 + Сz1 + D = 0. Следовательно, А(x - lA) + В(y - lB) + С (z - lC) + D = 0. Ах + Ву + Сz + D = l (A2 + B2 + C2).
Так как A2 + B2 + C2 > 0, то знак Ах + Ву + Сz + D совпадает со знаком l.
Итак, Ах + Ву + Сz + D > 0 Û точки М лежат в одной открытой полуплоскости с границей П, а именно в той, в сторону которой направлен вектор 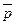 . Ах + Ву + Сz + D > 0 Û точки М лежат в другой открытой полуплоскости с этой же границей. . Ах + Ву + Сz + D > 0 Û точки М лежат в другой открытой полуплоскости с этой же границей.
Неравенства Ах + Ву + Сz + D ³ 0 и Ах + Ву + Сz + D £ 0 определяют замкнутые полуплоскости (их называют просто полуплоскости) с границей П.
Задача 20. Какую фигуру задаёт в аффинной системе координат система  ? ?
Решение. Уравнение x + z - 2 = 0 задаёт плоскость П1, параллельную оси (Оу) и пересекающую оси (Ох) и (Оz) в точках (2, 0, 0) и (0, 0, 2) соответственно. Неравенство 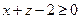 задаёт полуплоскость с границей П1, в которой не лежит начало координат (ибо координаты начала координат не удовлетворяют этому неравенству). Уравнение 2x + y - 4 = 0 определяет плоскость П2, параллельную оси (Оz) и пересекающую оси (Ох) и (Оу) в точках (2, 0, 0) и (0, 4, 0). Неравенство задаёт полуплоскость с границей П1, в которой не лежит начало координат (ибо координаты начала координат не удовлетворяют этому неравенству). Уравнение 2x + y - 4 = 0 определяет плоскость П2, параллельную оси (Оz) и пересекающую оси (Ох) и (Оу) в точках (2, 0, 0) и (0, 4, 0). Неравенство
| 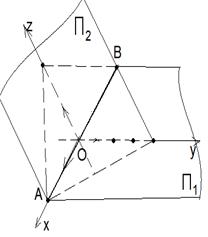
| 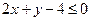 задаёт полуплоскость с границей П2 , в которой не лежит начало координат. Плоскости П1 и П2 пересекаются по прямой АВ. Данная система задаёт пару вертикальных двугранных углов с гранями П1 и П2, ни в одном из которых не лежит начало координат. задаёт полуплоскость с границей П2 , в которой не лежит начало координат. Плоскости П1 и П2 пересекаются по прямой АВ. Данная система задаёт пару вертикальных двугранных углов с гранями П1 и П2, ни в одном из которых не лежит начало координат.
IV. ОБРАЗЫ ВТОРОГО ПОРЯДКА
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


 , П : Ах + Ву + Сz + D = 0, М(х0, у0, z0).
Найти расстояние d(M0, П) от точки М0 до плоскости П.
Из уравнения плоскости П следует, что вектор
, П : Ах + Ву + Сz + D = 0, М(х0, у0, z0).
Найти расстояние d(M0, П) от точки М0 до плоскости П.
Из уравнения плоскости П следует, что вектор 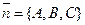 перпендикулярен плоскости П. Опустим из точки М0 перпендикуляр NM0 на плоскость П (рис. 51). Пусть N(x1, y1, z1). Тогда Ax1 + By1 + Cz1 + D = 0 (*). Искомое расстояние
d(M0, П) =
перпендикулярен плоскости П. Опустим из точки М0 перпендикуляр NM0 на плоскость П (рис. 51). Пусть N(x1, y1, z1). Тогда Ax1 + By1 + Cz1 + D = 0 (*). Искомое расстояние
d(M0, П) = 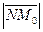 (**)
(**)
 Рис. 51
Рис. 51
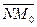 коллинеарен с вектором
коллинеарен с вектором 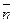 . Так как
. Так как 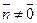 , то
, то 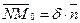 (***). Отсюда и из равенства (**) следует, что d(M0, П) =
(***). Отсюда и из равенства (**) следует, что d(M0, П) = 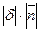 =
= 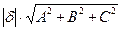 (****). Итак, задача свелась к нахождению d. Умножим скалярно на
(****). Итак, задача свелась к нахождению d. Умножим скалярно на 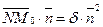 . Перейдя к координатам и учитывая, что система координат прямоугольная, получим
. Перейдя к координатам и учитывая, что система координат прямоугольная, получим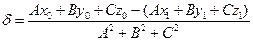 . Из равенства (*) следует, что
. Из равенства (*) следует, что 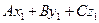 = -D. Итак,
= -D. Итак,  . Подставив d в (**), получим
. Подставив d в (**), получим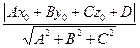 (52)
(52) . После упрощения получим
. После упрощения получим 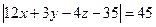 . Раскрывая модуль, получим уравнения двух плоскостей:
. Раскрывая модуль, получим уравнения двух плоскостей: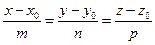 , М1(x1, y1, z1).
Найти расстояние d (M1, l).
Из уравнений прямой l следует, что точка M0 (x0, y0, z0 ) лежит на прямой l и вектор
, М1(x1, y1, z1).
Найти расстояние d (M1, l).
Из уравнений прямой l следует, что точка M0 (x0, y0, z0 ) лежит на прямой l и вектор 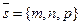 параллелен этой прямой. Искомое расстояние равно высоте параллелограмма,
параллелен этой прямой. Искомое расстояние равно высоте параллелограмма,
 Рис. 52
Рис. 52
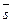 и
и 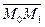 как на сторонах (рис. 52).
как на сторонах (рис. 52).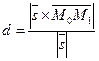 .
.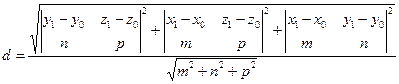 (53)
(53)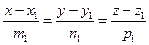 , l2 :
, l2 : 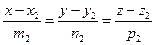 , l1 и l2 скрещиваются.
Найти d (l1, l2).
Из уравнений l1 и l2 следует, что M1 (x1, y1, z1) Î l1, M2 (x2, y2, z2)Î l2 и векторы
, l1 и l2 скрещиваются.
Найти d (l1, l2).
Из уравнений l1 и l2 следует, что M1 (x1, y1, z1) Î l1, M2 (x2, y2, z2)Î l2 и векторы 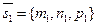 и
и  параллельны
параллельны
 Рис. 53
Рис. 53
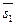 ,
, 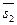 и
и 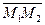 . Следовательно,
. Следовательно,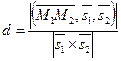 .
.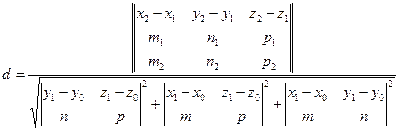 (54)
(54)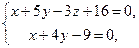 l2 :
l2 : 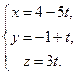
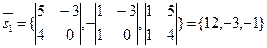 , М1 = {1, 2, 9}. Из уравнений l2 следует, что М2 (4, -1, 0) и
, М1 = {1, 2, 9}. Из уравнений l2 следует, что М2 (4, -1, 0) и 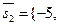 1, 3}.
1, 3}.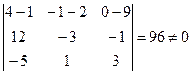 . Следовательно, l1 и l скрещиваются. Найдём
. Следовательно, l1 и l скрещиваются. Найдём 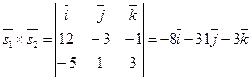 . Следовательно,
. Следовательно,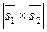 =
= 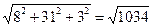 и
и 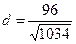 .
.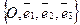 , Ах + Ву + Сz + D ³ 0.
Исследовать, какую фигуру задаёт данное неравенство.
Уравнение Ах + Ву + Сz + D = 0 задаёт плоскость. Пусть это плоскость П. Рассмотрим все точки пространства, не лежащие на П.
Вектор
, Ах + Ву + Сz + D ³ 0.
Исследовать, какую фигуру задаёт данное неравенство.
Уравнение Ах + Ву + Сz + D = 0 задаёт плоскость. Пусть это плоскость П. Рассмотрим все точки пространства, не лежащие на П.
Вектор 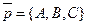 не параллелен плоскости П. Действительно, если бы
не параллелен плоскости П. Действительно, если бы 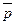 был параллелен П, то А×А + В×В + С×С = А2 + В2 + С2= 0. Но это невозможно.
был параллелен П, то А×А + В×В + С×С = А2 + В2 + С2= 0. Но это невозможно.
 Рис. 54
Рис. 54
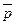 , и пусть она пересекает П в точке N. Векторы
, и пусть она пересекает П в точке N. Векторы 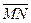 и
и 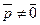 , следовательно,
, следовательно, 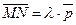 . (*) Очевидно, l > 0 Û когда точки М лежат в одной открытой полуплоскости с границей П, а именно в той, в сторону которой направлен вектор
. (*) Очевидно, l > 0 Û когда точки М лежат в одной открытой полуплоскости с границей П, а именно в той, в сторону которой направлен вектор 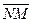 = {x - x1, y - y1, z - z1}. Равенство (*) в координатах перепишется:
= {x - x1, y - y1, z - z1}. Равенство (*) в координатах перепишется: ?
?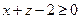 задаёт полуплоскость с границей П1, в которой не лежит начало координат (ибо координаты начала координат не удовлетворяют этому неравенству). Уравнение 2x + y - 4 = 0 определяет плоскость П2, параллельную оси (Оz) и пересекающую оси (Ох) и (Оу) в точках (2, 0, 0) и (0, 4, 0). Неравенство
задаёт полуплоскость с границей П1, в которой не лежит начало координат (ибо координаты начала координат не удовлетворяют этому неравенству). Уравнение 2x + y - 4 = 0 определяет плоскость П2, параллельную оси (Оz) и пересекающую оси (Ох) и (Оу) в точках (2, 0, 0) и (0, 4, 0). Неравенство

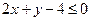 задаёт полуплоскость с границей П2 , в которой не лежит начало координат. Плоскости П1 и П2 пересекаются по прямой АВ. Данная система задаёт пару вертикальных двугранных углов с гранями П1 и П2, ни в одном из которых не лежит начало координат.
задаёт полуплоскость с границей П2 , в которой не лежит начало координат. Плоскости П1 и П2 пересекаются по прямой АВ. Данная система задаёт пару вертикальных двугранных углов с гранями П1 и П2, ни в одном из которых не лежит начало координат.