
|
|
Умножение вектора на действительное числоАНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ (для направления «Прикладная математика и информатика)
I. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ Геометрические векторы Определение 1. Геометрический отрезок называется ориентированным, если указан порядок его концов. Определение 2. Геометрическим вектором (вектором) называется ориентированный отрезок. При этом начало и конец ориентированного отрезка называются соответственно началом и концом вектора. Длина ориентированного отрезка называется длиной вектора. Вектор обозначается Определение 3. Два вектора называются равными, если они либо оба нулевые, либо имеют одинаковые длину и направление. Равенство векторов обладает следующими очевидными свойствами: 1) рефлексивность (всякий вектор равен сам себе); 2) симметричность ( если Множество всех равных векторов можно задать 1) одним из векторов (ориентированным отрезком); 2) упорядоченной парой точек; 3) длиной и направлением (в случае ненулевого вектора).
А равно Замечание. Часто бывает удобно все равные векторы считать за один вектор. В этом случае можно определить равенство ориентированных отрезков. Это равенство будет отношением эквивалентности на множестве всех ориентированных отрезков. Следовательно, множество ориентированных отрезков будет разбиваться на классы эквивалентности. Определение 2 можно дать в следующем виде. Определение 21. Геометрическим вектором называется класс ориентированных отрезков. При этом каждый отрезок из класса называется изображением вектора (слово «изображение» часто опускают).
Сложение векторов
10. Для любых двух векторов их сумма определена и однозначна. (Следует из определения). 20. 30. Для любого вектора 40. Доказательство. В случае, когда хотя бы один из векторов нулевой, утверждение следует из предыдущего свойства. Остаётся рассмотреть ненулевые векторы. При этом возможны следующие случаи.
поэтому сонаправлены между собой. Очевидно, в) Случай, когда векторы Определение 4. Векторы называются коллинеарными, если их можно отложить на одной прямой. Очевидно, два вектора неколлинеарны тогда и только тогда, когда они ненулевые и не параллельные. Из случая а) проведённого доказательства следует ещё одно правило сложения неколлинеарных векторов: Чтобы сложить два неколлинеарных вектора, достаточно отложить их от одной точки, построить на них, как на сторонах, параллелограмм, тогда диагональ этого параллелограмма, идущая из данной точки, будет задавать вектор суммы.
Теорема 1. Множество всех геометрических векторов есть аддитивная абелева группа. Определение 5.Разностью упорядоченной пары векторов называется сумма первого вектора и вектора, противоположного второму, т.е.
10. Для любой упорядоченной пары векторов их разность определена и однозначна. 20. Разность двух векторов антикоммутативна.
30. Не выполняется ассоциативный закон, а именно
Задача 1. АВСDA1B1C1D1 - параллелепипед,
Умножение вектора на действительное число Определение 6. Произведением ненулевого вектора
Если Свойства операции умножения вектора на действительное число. 10. Произведение любого вектора на любое действительное число определено и однозначно. 20. 1 30. Доказательство. Возможны случаи. 1) a = 0, или b = 0, или 2) a ¹ 0, b ¹ 0 и
Следовательно, а) a и b одного знака (пусть a > 0, b > 0). В этом случае a × b > 0.
Итак, левая и правая части доказываемого равенства имеют одинаковые длины и направления, поэтому они равны. б) a и b имеют разные знаки (пусть a > 0, b < 0). В этом случае a × b < 0.
Снова получили, что левая и правая части доказываемого равенства имеют одинаковые длины и направления, поэтому они равны. 40. Теорема 2. Множество всех геометрических векторов есть векторное (линейное) пространство над полем действительных чисел. Доказательство следует из теоремы 1 и свойств 10 – 40 операции умножения вектора на действительное число. Коллинеарные векторы Определение 7. Векторы называются коллинеарными, если их можно отложить на одной прямой. Свойства коллинеарных векторов. 10. Нулевой вектор коллинеарен с любым вектором. 20. Противоположные векторы коллинеарны. 30. При сложении двух коллинеарных векторов получается вектор, коллинеарный с данными векторами. Следовательно, множество коллинеарных векторов замкнуто относительно операции сложения. 40. Если вектор умножить на действительное число, то получится вектор, коллинеарный данному. Следовательно, множество коллинеарных векторов замкнуто относительно операции умножения на действительное число. Из этих свойств вытекает Теорема 3. Множество всех коллинеарных векторов есть векторное (линейное) пространство над полем действительных чисел. 50. Если два вектора коллинеарны, то хотя бы один из них можно представить в виде произведения другого на действительное число. Доказательство. Пусть векторы Из двух последних свойств следуют следующие два свойства. 60. (Необходимое и достаточное условие коллинеарности двух векторов) Два вектора коллинеарны тогда и только тогда, когда хотя бы один из них можно представить в виде произведения другого на действительное число. 70. Если вектор Следствие. Множество всех коллинеарных векторов есть одномерное векторное пространство над полем действительных чисел. Базисом в нём является любой его ненулевой вектор. Задача 2. Отрезок АВ точками С, Р, О, К, М, Т разбит на семь равных частей. Пусть
1.5. Компланарные векторы Определение 8. Векторы называются компланарными, если их можно отложить в одной плоскости. Свойства компланарных векторов. 10. Коллинеарные векторы компланарны. Иными словами, во множество всех возможных компланарных между собой векторов вместе с каждым его вектором входят все векторы, коллинеарные с ним. В частности, нулевой вектор содержится в любом таком множестве и вместе с каждым вектором в это множество входит противоположный ему вектор. Отсюда же следует, что множество компланарных векторов замкнуто относительно операции умножения на действительное число. 20. Сумма двух векторов есть вектор, компланарный с ними. Следовательно, множество компланарных векторов замкнуто относительно операции сложения. 30. Три вектора компланарны тогда и только тогда, когда хотя бы один из них можно представить в виде линейной комбинации двух других. Доказательство. Þ Пусть векторы 1) Среди данных векторов есть хотя бы одна пара коллинеарных векторов. Пусть
Ü Пусть 40. Если векторы Теорема 4. Множество всех компланарных векторов есть двумерное векторное пространство над полем действительных чисел. Базисом в нём является любая упорядоченная пара неколлинеарных векторов. Доказательство следует изпредыдущих свойств. Задача 3.АВСD и AB1C1D1 - два произвольных параллелограмма.
Теорема 5. Если векторы Доказательство. Пусть векторы 1) Вектор
Теорема 6. Множество всех геометрических векторов есть трёхмерное векторное пространство над полем действительных чисел. Базисом в нём является любая упорядоченная тройка некомланарных векторов. Доказательство следует из теоремы 5 и свойств компланарных векторов. В курсе линейной алгебры (в первом семестре) введены координаты вектора в данном базисе и рассмотрены свойства координат. Все определения и свойства их будут использоваться в векторных пространствах геометрических векторов. Если в векторном пространстве зафиксированы два базиса В и В1, Т – матрица перехода от базиса В к базису В1, х и х1 столбцы координат данного вектора
Во множестве всех геометрических векторов

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
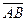 , где А – начало, а В – конец вектора. Если начало и конец вектора нас не интересуют, то вектор обозначают
, где А – начало, а В – конец вектора. Если начало и конец вектора нас не интересуют, то вектор обозначают  . Длина вектора обозначается
. Длина вектора обозначается  или
или  . Если начало и конец вектора совпадают, то вектор называют нулевым и обозначают
. Если начало и конец вектора совпадают, то вектор называют нулевым и обозначают 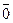 . Если начало и конец вектора – различные точки (А ¹ В), то существует и только один луч с началом А, проходящий через точку В. Этот луч задаёт в пространстве направление, которое называется направлением данного вектора. Нулевой вектор не имеет направления.
. Если начало и конец вектора – различные точки (А ¹ В), то существует и только один луч с началом А, проходящий через точку В. Этот луч задаёт в пространстве направление, которое называется направлением данного вектора. Нулевой вектор не имеет направления. , то
, то 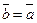 ); 3) транзитивность (если
); 3) транзитивность (если 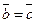 , то
, то  ).
). , то существует и только один вектор с началом в точке А, равный данному вектору. Это вектор
, то существует и только один вектор с началом в точке А, равный данному вектору. Это вектор  (т.е. В = А). Если
(т.е. В = А). Если  , то существует и только один луч, сонаправленный с вектором
, то существует и только один луч, сонаправленный с вектором 
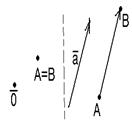 Рис. 1
Рис. 1
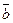 - любые два вектора. Чтобы к вектору
- любые два вектора. Чтобы к вектору  ), от конца В полученного вектора отложить вектор
), от конца В полученного вектора отложить вектор  ). Тогда вектор
). Тогда вектор 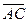 будет вектором суммы, т.е.
будет вектором суммы, т.е.
 . Иными словами,
. Иными словами,  .
Свойства сложения векторов.
.
Свойства сложения векторов.
 Рис. 2
Рис. 2
 =
= 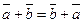 для любых векторов
для любых векторов  . Отложим от точки А вектор
. Отложим от точки А вектор  . Так как
. Так как 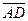 и
и  имеют одинаковые длины и направления, то АВСD – параллелограмм. Следовательно, отрезки АВ и DC тоже имеют одинаковые длины и направления. Итак,
имеют одинаковые длины и направления, то АВСD – параллелограмм. Следовательно, отрезки АВ и DC тоже имеют одинаковые длины и направления. Итак,  . По правилу сложения векторов
. По правилу сложения векторов
 Рис. 3
Рис. 3
 и
и 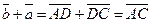 . Отсюда
. Отсюда  (рис.4). Векторы
(рис.4). Векторы  сонаправлены с вектором
сонаправлены с вектором 
 Рис. 4
Рис. 4
 . Следовательно,
. Следовательно,  , т.е.
, т.е.  для любых векторов
для любых векторов  Доказательство. Для левой части получим
Доказательство. Для левой части получим
 . Для правой части
. Для правой части  . Итак, результаты равны.
Из свойств 10 – 50 вытекает
. Итак, результаты равны.
Из свойств 10 – 50 вытекает
 Рис. 5
Рис. 5
 .
. Рис. 6
Рис. 6
 для любых векторов
для любых векторов  для любых векторов
для любых векторов  .
. =
=  ,
,  ,
, 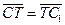 ,
,
 ,
,  ,
,
 . Найдите
1)
. Найдите
1)  ; 2)
; 2)  .
Решение. 1)Так как
.
Решение. 1)Так как 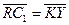 ,
,  ,
,  , то
, то 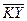 +
+  +
+ 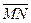 =
=  .
2) Так как
.
2) Так как  и
и  , то
, то
 .
.
 Рис. 7
Рис. 7
 ), что
), что ,
,

 для любого вектора
для любого вектора  для любого вектора
для любого вектора 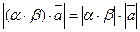 ,
,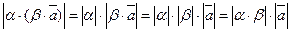 .
. . Так как направления векторов зависят от знаков коэффициентов, то рассмотрим все возможные случаи.
. Так как направления векторов зависят от знаков коэффициентов, то рассмотрим все возможные случаи. ,
, , следовательно,
, следовательно,  .
. .
. .
. и (
и (  для любых векторов
для любых векторов 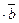 . Если
. Если 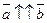 , то
, то  . Если
. Если 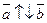 , то
, то  . Иными словами, для задания множества всех коллинеарных векторов достаточно задать один ненулевой из них.
. Иными словами, для задания множества всех коллинеарных векторов достаточно задать один ненулевой из них. . Выразить через вектор
. Выразить через вектор  .
Решение.
.
Решение.  ,
, 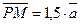 ,
,  ,
,  ,
,  .
.
 Рис. 8
Рис. 8
 компланарны. Возможны два случая.
компланарны. Возможны два случая. , т.е. вектор
, т.е. вектор  ,
,  ,
,  . Отрезки ОА, ОВ, ОС попарно не параллельны. Проведём СD ïïОА так, что D Î ОВ (прямой ОВ). Тогда получим
. Отрезки ОА, ОВ, ОС попарно не параллельны. Проведём СD ïïОА так, что D Î ОВ (прямой ОВ). Тогда получим 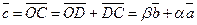 , т.е. вектор
, т.е. вектор  Рис. 9
Рис. 9
 . По свойствам 10 и 20 следует, что вектор
. По свойствам 10 и 20 следует, что вектор 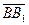 ,
,  ,
,  параллельны одной плоскости.
Решение. Для решения задачи достаточно показать, что эти векторы компланарны.
параллельны одной плоскости.
Решение. Для решения задачи достаточно показать, что эти векторы компланарны.
 ;
;
 ;
;
 =
= (
=
= (  ) + (
) + (  ) = =
) = =  . Так как
. Так как  , то эти векторы компланарны .
, то эти векторы компланарны .
 Рис. 10
Рис. 10
 - любой вектор. Возможны два случая.
- любой вектор. Возможны два случая. .
. ,
,  ,
,  и
и  (рис. 11). Проведём (DM) ||
(рис. 11). Проведём (DM) ||  . Но
. Но  коллинеарен вектору
коллинеарен вектору 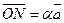 . Аналогично,
. Аналогично,  ,
,  . Следовательно,
. Следовательно,  .
.
 Рис. 11
Рис. 11
 где
где 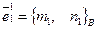 ,
,  .
.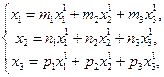 где
где  ,
,  ,
, 