
|
|
Геометрический смысл векторного произведенияБилет 1 Прямоугольная декартова система координат на плоскости Прямоугольной ДСК на плоскости называют две взаимно перпендикулярные координатные оси с общим началом и одинаковой масштабной единицей. Ox – ось абсцисс, Oy – ось ординат. Координатой точки на плоскости называют пару чисел x и y, где Прямоугольная система координат в пространстве (в этом параграфе имеется в виду трехмерное пространство, о более многомерных пространствах — см. ниже) образуется тремя взаимно перпендикулярными осями координат
Рис. 2 Положение точки Координата координата
Символически это записывают так: или привязывают запись координат к конкретной точке с помощью индекса:
Прямоугольные все системы координат в трехмерном пространстве делятся на два класса — правые (также используются термины положительные, стандартные) и левые. Обычно по умолчанию стараются использовать правые координатные системы, а при их графическом изображении еще и располагать их если можно, в одном из нескольких обычных (традиционных) положений. (На рис. 2 изображена правая координатная система). Правую и левую системы координат невозможно поворотами[3] совместить так, чтобы совпали соответствующие оси (и их направления). Определить, к какому классу относится какая-либо конкретно взятая система координат можно используя правило правой руки, правило винта итп (положительное направление осей выбирают так, чтобы при повороте оси Билет 2
1. Пусть даны две точки Согласно теореме Пифагора, 2. Деление отрезка в данном отношении. Говорят, что точка C делит отрезок AB внутренним образом, если C лежит внутри AB и внешним, если C лежит вне AB. Говорят, что точка C делит отрезок AB в отношении l, если Замечание: Пусть даны две точки: В системе из трёх материальных точек, имеющих x=(m1*x1+m2*x2+x3*m3)/(m1+m2+m3);
Билет 3 Полярная система координат Полярной системой координат называют точку O (полюс) и луч Ox (полярная ось), выходящий из этой точки с масштабной единицей. Полярными координатами точки M называют пару чисел r и j, где r - расстояние от M до полюса, j - угол между радиус-векторами OM и Ox, отсчитываемый от полярной оси против часовой стрелки ( Связь между декартовыми и полярными координатами: Цилиндрической системой координат называют трёхмерную систему координат, являющуюся расширением полярной системы координат путём добавления третьей координаты (обычно обозначаемой Точка
При использовании в физических науках и технике международный стандарт ISO 31-11 рекомендует использовать обозначения Некоторые математики используют Цилиндрические координаты удобны при анализе поверхностей, симметричных относительно какой-либо оси, если ось Сферическими координатами называют систему координат для отображения геометрических свойств фигуры в трёх измерениях посредством задания трёх координат Понятия зенит и азимут широко используются в астрономии. Вообще зенит — это направление вертикального подъёма над произвольно выбранной точкой (точкой наблюдения), принадлежащей так называемой фундаментальной плоскости. В качестве фундаментальной плоскости в астрономии может быть выбрана плоскость, в которой лежит экватор, или плоскость, в которой лежит горизонт, или плоскость эклиптики и т. д., что порождает разные системы небесных координат. Азимут — угол между произвольно выбранным лучом фундаментальной плоскости с началом в точке наблюдения и другим лучом этой плоскости, имеющим общее начало с первым. Применительно к нашему рисунку сферической системы координат, фундаментальная плоскость — это плоскость xy. Зенит — некая удалённая точка, лежащая на оси Z и видимая из начала координат. Азимут отсчитывается от оси X до проекции радиус-вектора r на плоскость xy. Это объясняет названия углов, как и то, что сферическая система координат может служить обобщением (пусть хотя бы и приближённым) множества видов систем небесных координат.
Угол Зависимо или независимо от стандарта (ISO 31-11), существует и такое соглашение или конвенция (англ. convention), когда вместо зенитного угла Тогда углы Билет 5 Векторная алгебра Основные понятия: Вектором называют отрезок прямой, если указано, какая из его граничных точек является началом, а какая – концом.
Коллинеарными называют векторы, лежащие на параллельных прямых. Компланарными – лежащие на одной или параллельных плоскостях. Равными называют векторы сонаправленные и имеющие одинаковую длину. Противоположные – противоположно направленные и имеющие одинаковую длину. Ортом Угол между векторами: cosw= ab/|a|*|b| в координатах же : cosw= ( x1x2+y1y2+z1z2)/(sqrt(x1^2+y1^2+z1^2)+sqrt(x2^2+y2^2+z2^2))
Билет 6 Линейные операции над векторами: 1. Сложение векторов выполняется по правилу треугольника или параллелограмма. 2. Умножение вектора на число. Произведением вектора Линейной комбинацией векторов Если
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому вектору. Необходимое и достаточное условие коллинеарности двух векторов: Для того чтобы 1. Пусть 2. Пусть Любой вектор на плоскости может быть единственным образом по двум неколлинеарным векторам. Из рисунка видно, что такое разложение существует. Докажем единственность. Действительно, Пусть также
Билет 7 Любой вектор в пространстве может быть единственным образом разложен по трём некомпланарным векторам. Доказывается аналогично. Совокупность векторов, обладающих двумя свойствами: любой вектор может быть выражен через эти вектора и это выражение будет единственным, называется базисом. Таким образом, базис образуют любые два неколлинеарных вектора на плоскости и любые три некомпланарных в пространстве. Пусть Базис образует аффинную систему координат. Углом между векторами называют наименьший из углов, на который надо повернуть один вектор до совмещения с другим по приведения из к общему началу. Обозначение: Орт оси – единичный вектор, сонаправленный с осью. Углом между вектором и осью называют угол между вектором и ортом оси.
Свойства проекции вектора на ось: 1. 2. 3. Координаты вектора в прямоугольной декартовой системе координат ДСК – частный случай аффинной системы координат. Разложим Направляющие косинусы вектора в прямоугольной декартовой системе координат Пусть a, b и g - углы, которые образует Если даны две точки М1 и М2 , являющиеся соответственно началом и концом вектора а, то его коорлинаты X Y Z вычисляются по вормулам X=x2-x1 Y=y2-y1 Z=z2-z1 . Формула |a|=Sqrt(X^2+Y^2+Z^2) позволяет по координатам вектора определить его модуль. Если q w e – углы, которые состовляют вектор а с координатными осями, то cos q cos w cos e называются направляющими косинусами вектора а. Вследствии X=|a|cosq Y=|a|cosw Z=|a|cose Отсюда следует, что cos^2q+cos^2w+cos^2e=1 Аффинная система координат (косоугольная система координат) — прямолинейная система координат в аффинном пространстве. В
Tочку На аффинной плоскости
Линейные операции над векторами в аффинных координатах Пусть Свойства линейных операций: 1. 2. 3. 4. для 5. 6. 7. 8. Пусть в пространстве выбран базис
Билет 8 Скалярное произведение Скалярным произведением Второе определение: Оба определения равносильны, т.к. Алгебраические свойства скалярного произведения: 1. 2. 3. 4. 5. Геометрические свойства скалярного произведения С помощью скалярного произведения можно находить основные метрические величины: длины отрезков (или, что то же самое, длины векторов) и величины углов. 1. Длина вектора а находится по формуле: 2. Величина
— ненулевые векторы — угол между ненулевыми векторами — угол между ненулевыми векторами Алгебраическое значение длины ортогональной проекции вектора Ортогональная проекция вектора Если ось задается единичным вектором Необходимое и достаточное условие ортогональности двух векторов: Дл того чтобы 1.Если 1. Пусть 2. Пусть Пусть задана прямоугольная декартова система координат
Билет 9 Векторное произведение векторов Три вектора называют упорядоченной тройкой векторов, если указано, какой из них первый, какой второй и какой третий. Некомпланарная тройка векторов Векторным произведение Алгебраические свойства: 1. 2. 3. 4. Необходимое и достаточное условие коллинеарности двух векторов: Для того чтобы 1. Пусть 2. Пусть Модуль векторного произведение равен площади параллелограмма, построенного на этих векторах.
Выражение векторного произведения в ДСК
Если в ДСК Геометрический смысл векторного произведения 1. Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения. 2. Длина (модуль) векторного произведения
2. Длина (модуль) векторного произведения
Смешанное произведение трёх векторов Смешанным произведением векторов
Пусть в ДСК Билет 10 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

 . Записываются так:
. Записываются так:  .
. ,
,  и
и 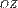 . Оси координат пересекаются в точке
. Оси координат пересекаются в точке  , которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно (не обязательно[2]) одинаковы для всех осей.
, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно (не обязательно[2]) одинаковы для всех осей.  — ось абсцисс,
— ось абсцисс,  — ось ординат,
— ось ординат, 

 в пространстве определяется тремя координатами
в пространстве определяется тремя координатами  ,
,  и
и  . Координата
. Координата  равна длине отрезка
равна длине отрезка  , координата
, координата  — длине отрезка
— длине отрезка  , координата
, координата  — длине отрезка
— длине отрезка 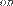 в выбранных единицах измерения. Отрезки
в выбранных единицах измерения. Отрезки  и
и  определяются плоскостями, проведёнными из точки
определяются плоскостями, проведёнными из точки  параллельно плоскостям
параллельно плоскостям  ,
, 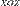 и
и 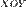 соответственно.
соответственно. называется абсциссой точки
называется абсциссой точки  ,
, координата
координата  — аппликатой точки
— аппликатой точки  .
. Или
Или 
 и т. п.
и т. п. Каждая ось рассматривается как числовая прямая, т. е. имеет положительное направление, а точкам, лежащим на отрицательном луче приписываются отрицательные значения координаты (расстояние берется со знаком минус). То есть, если бы, например, точка
Каждая ось рассматривается как числовая прямая, т. е. имеет положительное направление, а точкам, лежащим на отрицательном луче приписываются отрицательные значения координаты (расстояние берется со знаком минус). То есть, если бы, например, точка  лежала не как на рисунке — на луче
лежала не как на рисунке — на луче  , а на его продолжении в обратную сторону от точки
, а на его продолжении в обратную сторону от точки 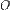 (на отрицательной части оси
(на отрицательной части оси  ), то абсцисса
), то абсцисса 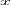 точки
точки  ). Аналогично и для двух других осей.
). Аналогично и для двух других осей. против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси
против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси  , если этот поворот наблюдать со стороны положительного направления оси
, если этот поворот наблюдать со стороны положительного направления оси 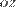 ).
). Простейшие задачи аналитической геометрии
Простейшие задачи аналитической геометрии и
и 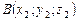 . Найти расстояние между ними.
. Найти расстояние между ними. .
. . При этом, если
. При этом, если  , то
, то  , иначе
, иначе  .
. и
и  .
. и
и  и пусть C делит AB в отношении l. Найдём точку C. Пусть
и пусть C делит AB в отношении l. Найдём точку C. Пусть  . Тогда по теореме Фаллеса
. Тогда по теореме Фаллеса  , и
, и  .
. ,
,  ).
). ,
, 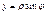 .
. даётся как
даётся как  . В терминах прямоугольной системы координат:
. В терминах прямоугольной системы координат: — расстояние от
— расстояние от  до
до  , ортогональной проекции точки
, ортогональной проекции точки  на плоскость
на плоскость  . Или то же самое, что расстояние от
. Или то же самое, что расстояние от  до оси
до оси  .
. — угол между осью
— угол между осью  и отрезком
и отрезком  .
. .
.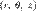 .
. взять в качестве оси симметрии. Например, бесконечно длинный круглый цилиндр в прямоугольных координатах имеет уравнение
взять в качестве оси симметрии. Например, бесконечно длинный круглый цилиндр в прямоугольных координатах имеет уравнение  , а в цилиндрических — очень простое уравнение
, а в цилиндрических — очень простое уравнение  . Отсюда и идёт для данной системы координат имя «цилиндрическая».
. Отсюда и идёт для данной системы координат имя «цилиндрическая». , где
, где  — расстояние до начала координат, а
— расстояние до начала координат, а  и
и  — зенитный и азимутальный угол соответственно.
— зенитный и азимутальный угол соответственно. ОпределенияТри координаты
ОпределенияТри координаты  определены как:
определены как: — расстояние от начала координат до заданной точки
— расстояние от начала координат до заданной точки  .
. — угол между осью
— угол между осью  — угол между осью
— угол между осью  и проекцией отрезка, соединяющего начало координат с точкой
и проекцией отрезка, соединяющего начало координат с точкой  (в Америке углы
(в Америке углы  и
и 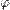 меняются ролями[источник не указан 292 дня]).
меняются ролями[источник не указан 292 дня]). называется зенитным, или полярным, или нормальным, а также он может быть назван английским словом colatitude, а угол
называется зенитным, или полярным, или нормальным, а также он может быть назван английским словом colatitude, а угол  — азимутальным. Углы
— азимутальным. Углы  и
и  , а
, а  (то есть при
(то есть при  или
или  ).
). —
—  . В этом случае он будет изменяться в пределах
. В этом случае он будет изменяться в пределах  .
. и
и  , так же как и в первом случае, а
, так же как и в первом случае, а  , (уже при
, (уже при 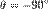 или
или  ).
). , если начало совпадает с концом.
, если начало совпадает с концом. называют единичный вектор, сонаправленный с
называют единичный вектор, сонаправленный с  такой, что
такой, что  и
и  , если
, если  и
и  , если
, если  , то
, то  . У
. У  произвольное направление.
произвольное направление. называют сумму произведений этих векторов на произвольные числа:
называют сумму произведений этих векторов на произвольные числа:  .
. , то говорят, что
, то говорят, что  и
и  были коллинеарны, необходимо и достаточно, чтобы
были коллинеарны, необходимо и достаточно, чтобы  .
. .
. и
и  и
и  . Очевидно, что l существует.
. Очевидно, что l существует. ,
,  , следовательно
, следовательно 
 , где
, где  . Вычтем из первого уравнения второе. Получим:
. Вычтем из первого уравнения второе. Получим:  . Т.к.
. Т.к.  , то
, то  , т.е.
, т.е.  , что противоречит условию.
, что противоречит условию. - базис в пространстве и вектор
- базис в пространстве и вектор  . Тогда числа a, b и g называют координатами вектора
. Тогда числа a, b и g называют координатами вектора 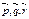 .
. .
.
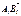 - геометрическая проекция
- геометрическая проекция  на ось l.
на ось l. - скалярная проекция
- скалярная проекция  на ось l.
на ось l.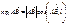 .
. .
. .
. по базису
по базису  , который образует декартову систему координат и центр которого совпадает с началом вектора
, который образует декартову систему координат и центр которого совпадает с началом вектора  :
:  . Здесь x, y и z – координаты вектора в базисе. Тогда
. Здесь x, y и z – координаты вектора в базисе. Тогда  ,
,  ,
,  .
. с осями ДСК (Ox, Oy и Oz). Тогда
с осями ДСК (Ox, Oy и Oz). Тогда  ,
,  и
и  называют направляющими косинусами
называют направляющими косинусами  . Пусть x, y и z – координаты вектора
. Пусть x, y и z – координаты вектора  ,
,  ,
,  ,
, 
 ,
, 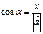 ,
,  ,
, 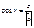 .
. -мерном пространстве она задаётся упорядоченной системой линейно независимых векторов
-мерном пространстве она задаётся упорядоченной системой линейно независимых векторов 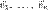 , выходящих из одной точки
, выходящих из одной точки  . Аффинными координатами точки
. Аффинными координатами точки  называют такие числа
называют такие числа  , что
, что
 и систему векторов
и систему векторов  называют репером или аффинным базисом; прямые, проходящие через вектора
называют репером или аффинным базисом; прямые, проходящие через вектора  — координатными осями.
— координатными осями.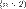 координату
координату  называют абсциссой, а
называют абсциссой, а  — ординатой точки
— ординатой точки  . В пространстве же координаты точки называют её абсциссой, ординатой и аппликатой. Аналогичным образом именуют и координатные оси.
. В пространстве же координаты точки называют её абсциссой, ординатой и аппликатой. Аналогичным образом именуют и координатные оси. 
 ,
,  .
. .
. .
. .
.
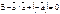 .
. .
. .
.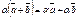 .
. .
. и пусть
и пусть  и
и 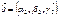 . Тогда
. Тогда  ,
,  ,
,  ,
,  . Таким образом,
. Таким образом,  ,
,  .
. .
. .
. ,
, 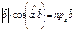 .
. .
. .
.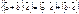 .
. , если
, если  , иначе
, иначе  .
. .
. угла между ненулевыми векторами находится по формуле:
угла между ненулевыми векторами находится по формуле: Отсюда заключаем, что:
Отсюда заключаем, что: и
и  перпендикулярны
перпендикулярны  тогда и только тогда, когда их скалярное произведение равно нулю:
тогда и только тогда, когда их скалярное произведение равно нулю:  ;
; и
и  острый
острый  тогда и только тогда, когда их скалярное произведение положительно;
тогда и только тогда, когда их скалярное произведение положительно; и
и  тупой
тупой  тогда и только тогда, когда их скалярное произведение отрицательно.
тогда и только тогда, когда их скалярное произведение отрицательно. на ось, задаваемую вектором .
на ось, задаваемую вектором . 

 , то .
, то .  Свойства 1 и 2 следуют непосредственно из определения скалярного произведения. Третье и четвертое свойства вытекают из геометрического смысла скалярного произведения (см. (1.8)) и п.1 замечаний 1.4.
Свойства 1 и 2 следуют непосредственно из определения скалярного произведения. Третье и четвертое свойства вытекают из геометрического смысла скалярного произведения (см. (1.8)) и п.1 замечаний 1.4.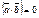 .
. или
или 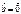 , то теорема справедлива, т.к. нулевой вектор имеет произвольное направление и
, то теорема справедлива, т.к. нулевой вектор имеет произвольное направление и  .
. . Тогда
. Тогда  и, т.к.
и, т.к.  и
и  , то
, то  , т.е.
, т.е.  .
. . Тогда
. Тогда  .
. и пусть
и пусть  и
и  . Тогда
. Тогда 
 , т.к.
, т.к.  ,
, 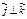 и
и 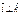 .
. называется правой (левой) если после приведения их к общему началу
называется правой (левой) если после приведения их к общему началу 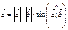 ,
,  ,
,  и векторы
и векторы  ,
, 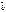 и
и  образуют правую тройку. Обозначение:
образуют правую тройку. Обозначение:  .
. .
. .
.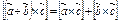 .
. .
. , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы 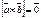 .
. ,
,  . Тогда
. Тогда  , т.е.
, т.е.  .
. . Тогда
. Тогда  .
.
 .
.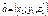 и
и 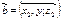 то
то  .
. 

 .
. x
x  равна площади S параллелограмма, построенного на приведенных к общему началу векторах
равна площади S параллелограмма, построенного на приведенных к общему началу векторах 
 x
x  равна площади S параллелограмма, построенного на приведенных к общему началу векторах
равна площади S параллелограмма, построенного на приведенных к общему началу векторах 
 ,
,  и
и  называют число
называют число  .
. Модуль смешанного произведения векторов равен объёму параллелепипеда, построенного на этих векторах после приведения их к общему началу.
Модуль смешанного произведения векторов равен объёму параллелепипеда, построенного на этих векторах после приведения их к общему началу. , где
, где  - орт
- орт  .
. ,
,  ,
,  . Тогда
. Тогда 
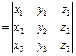 .
.