
|
|
Если прямые скрещиваются, то выполняются условия
Если прямые скрещиваются, то расстояние между ними равно расстоянию между параллельными плоскостями, проведенными через заданные прямые. Вектор нормали п этих плоскостей перпен-дикулярен векторам s1 и s2, следовательно, n= s1xs2 Так как P1(x1;y1;z1), P2(x2;y2;z2) -точки, принадлежащие прямым, расстояние между скрещивающимися прямыми вычисляем по формуле
Пусть в пространстве заданы канонические уравнения прямой l и общее уравнение плоскости pi:
Углом между прямой и плоскостью называется меньший из углов между прямой и ее проекцией на плоскость. Синус угла между прямой и плоскостью определяем по формуле
В координатной форме синус угла между прямой и плоскостью определяем по формуле
Для определения точки пересечения прямой с плоскостью решим систему уравнений плоскости и прямой, записав параметрические уравнения прямой:
Подставим x, y, z в уравнение плоскости и найдем параметр t. Найденное значение t = -(Ax1+By1+Cz1+D)/(mA+nB+pC) подставляем в параметрическое уравнение прямой и вычисляем координаты точки пересечения. Если mA+nB+pC<>0, то прямая пересекае плоскость в единственной точке. Условие параллельности прямой и плоскости: mA+nB+pС=0 и Ax1+By1+Cz1+D<>0 Условие ортогональности прямой и плоскости: m/A=n/B=p/C Условие принадлежноности прямой и плоскости: mA+nB+pС=0 и Ax1+By1+Cz1+D=0 Вычисление расстояния между параллельными прямыми:
Решение: Составим уравнение плоскости, проходящей через точкуP1(x1;y1;z1), принадлежащую первой прямой и перпендикулярной заданным прямым (n=s=(m2;n2;p2): m2(x-x1)+n2(y-y1)+p2(z-z1)). Записав параметрические уравнения второй прямой, найдем точку Р пересечения второй прямой и плоскости. Далее подставляя найденное значение t в параметрическое уравнение прямой, находим точку Р. Найдем вектор РР1, и расстояние между прямыми | РР1|. Эллипс: эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных точек, называемых фокусами эллипса, есть величина постоянная. F1, F2 – фокусы
Выведение канонического уравнения эллипса: Для любой точки М(х, y) эллипса по определению имеет место равенство |MF1|+|MF2|=2a, отсюда
Это и есть уравнение эллипса. Упростим его. Освободимся от радикалов. Перенесем второй корень в правую часть равенства и возведем обе части равенства в квадрат, одновременно раскрывая скобки и приводя подобные члены. Оставшийся радикал снова уединим в левую часть равенства.
Еще раз возведем в квадрат обе части уравнения, перенесем члены с текущими координатами в левую, а постоянные — в правую часть равенства.
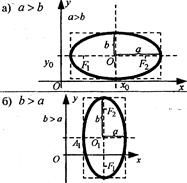
Свойства эллипса(x2/a2+y2/b2=1): 1.Сумма двух положительных слагаемых равна 1=> x2/a2<=1 и y2/b2<=1 => -a<=x<=a, -b<=y<=b, т.е. эллипс лежит внутри прямоугольника, определяемого этими неравенствами. 2. Т.к. уравнение содержит только квадраты текущих координат, т.е. точка (х, у) принадлежит эллипсу, то и точки (х, -у), (-х, у), (-х, -у) принадлежат эллипсу. Следовательно, эллипс имеет две оси симметрии — оси координат. Точка пересечения осей симметрии О называется центром эллипса. 3. Найдем точки пересечения эллипса с осями координат. При у=0 х = ±а, при х = 0 у=±b. Точки А1(-а, о), А2(а, о),В1(0, -b), В2(о, b) называются вершинами эллипса. Отрезки А1А2 и В1В2, а также их длины 2аи 2b называются большой и малой осями эллипса, а и b — полуосями. Достаточно построить кривую по точкам при х≥ 0, у ≥ 0 , а затем использовать симметрию. Замечание. Из соотношения между параметрами a2 - c2 = b2можно определить положение фокусов, построив прямоугольный треугольник по катету b и гипотенузе а (см. рис. 2).
Чем больше ε, тем больше расстояние от центра до фокусов и тем более сплющен эллипс. При ε = 0 b/a = 1, т. е. b = а, при этом эллипс превращается в окружность х2 + у2 = а. Замечание. Можно систему координат ввести иначе. Через фокусы провести ось Оу . Вид канонического уравнения в этом случае не изменится. Договоримся только, что полуось вдоль оси Ох обозначать через а, а вдоль оси Оу — через b( |MF1|+|MF2|=2b) Если в первом случае было а>b и a2 - c2 = b2,то теперь а<b и b2- c2 =a2. Гипербола:Из школьного курса математики известно, что кривая, задаваемая уравнением y=k/x , где k - число, называется гиперболой. Однако это - частный случай гиперболы (равносторонняя гипербола). Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная. Так же, как и в случае эллипса, для получения уравнения гиперболы выберем подходящую систему координат. Начало координат расположим на середине отрезка между фокусами, ось направим вдоль этого отрезка, а ось ординат -- перпендикулярно к нему. Теорема. Пусть расстояние между фокусами F1 и F2 гиперболы равно 2c, а абсолютная величина разности расстояний от точки гиперболы до фокусов равна 2a. Тогда гипербола в выбранной выше системе координат имеет уравнение (x2/a2-y2/b2=1), где b2= с2 - а2. Доказательство. Пусть M(x, y) - текущая точка гиперболы.
Так как разность двух сторон треугольника меньше третьей стороны, то |F1M- F2M|< F1F2 то есть a<c. В силу последнего неравенства вещественное число , определяемое формулой (12.9), существует. По условию, фокусы -- F1(-c; 0) F2(c; 0) , . По формуле (10.4) для случая плоскости получаем По определению гиперболы Это уравнение запишем в виде Обе части возведем в квадрат: После приведения подобных членов и деления на 4, приходим к равенству Опять обе части возведем в квадрат: Раскрывая скобку и приводя подобные члены, получим С учетом формулы Разделим обе части уравнения на a2b2 и каноническое уравнение гиперболы. Исследуем форму гиперболы: 1.Оси координат являются осями симметрии гиперболы. 2.Точки пересечения гиперболы с осями координат. Она пересекает ось Ох в двух точках, а ось Оу не пересекает. Обозначим их А1 и А2. Точки пересечения гиперболы с осью симметрии называются ее вершинами, а сама ось и отрезок А1А2 называются действительной осью гиперболы. Ось симметрии, которую гипербола на пересекает, называется мнимой осью гиперболы. Мнимой осью называется также отрезок В1В2, где В1 и В2расположены на мнимой оси по обе стороны от ее центра симметрии О на расстоянии b. 3. Покажите, что все точки гиперболы лежат вне полосы, ограниченной прямыми х=±а и, следовательно, гипербола состоит из двух отдельных ветвей. 4. Можно доказать, что при неограниченном удалении точек гиперболы от начала координат они неограниченно приближаются к прямым, проходящим через диагонали прямоугольникасо сторонами х = ±а и у = ±b, т. е. к прямым У = ±(b/a)*x, которые являются асимптотами гиперболы.
5. Теперь сделайте чертеж. Постройте прямоугольник со сторонами х = ±а, у = ±b, проведите его диагонали и продолжите их за вершины прямоугольника, постройте вершины гиперболы, а затем всю гиперболу (рис. 5). Эксцентриситет гиперболы ε=| F1F2|/| А1А2|, т.е. ε=с/a=(1+(b/a)^2)^0.5 > 1. Парабола В школьном курсе математики достаточно подробно изучалась парабола, которая, по определению, являлась графиком квадратного трехчлена. Здесь мы дадим другое (геометрическое) определение параболы. Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы. Чтобы получить уравнение кривой, соответствующей этому определению, введем подходящую систему координат. Для этого из фокуса F опустим перпендикуляр FD на директрису l. Начало координат O расположим на середине отрезка FD, ось Ox направим вдоль отрезка FD так, чтобы ее направление совпадало с направлением вектора DF. Ось Oy проведем перпендикулярно оси Ox.
ТеоремаПусть расстояние между фокусом F и директрисой l параболы равно P. Тогда в выбранной системе координат парабола имеет уравнение y2=2px Доказательство. В выбранной системе координат фокусом параболы служит точка F(p/2,0), а директриса имеет уравнение x=-p/2. Пусть M(x,y) -- текущая точка параболы. Тогда по формуле (10.4) для плоского случая находим
Расстоянием от точки M до директрисы l служит длина перпендикуляра MK, опущенного на директрису из точки M. Из рисунка очевидно, что M=x+p/2 . Тогда по определению параболы MK=FM, то есть
После приведения подобных членов получим каноническое уравнение. Свойства:
Если фокус перпендикулярно директрисе провести ось Оу, то уравнение параболы примет вид x2=-2рy.
Cмещенные кривые второго порядка:
Матрицей типа (или размера) m x n называют прямоугольную числовую таблицу, состоящую из mn чисел, которые расположены в m строках и n столбцах. Составляющие матрицу числа называют элементами матрицы. aij, где i – номер строки, j – номер столбца.
Типы матриц: 1)матрица размером 1 x n. (a11 a12 … a1n) матрица – строка, число n – длина строки. 2)матрица размером m x 1 – матрица – столбец. Число m – высота матрицы.
6) Если в диагональной матрице порядка n на диагонали стоят единицы, то её называют единичной. Для обозначения единичной матрицы обычно используется буква 7)Квадратная матрица называется верхней треугольной (нижней треугольной), если все ее элементы, стоящие ниже (выше) главной диагонали, равны нулю. Например, верхние треугольные матрицы:
Нижние треугольные матрицы:
Верхняя треугольная матрица иногда называется правой треугольной, а нижняя треугольная - левой треугольной. 8) Матрица называется ступенчатой, если для любой её строки выполнено следующее её условие: под первым слева нулевым элементом строки предшествующими ему нулевыми элементами строки все элементы матрицы равны нулю.
Две матрицы называются равными, если они имеют один и тот же тип и если у них совпадают соответствующие элементы.
Сложение. Сложение определено только для матриц одинаковых размеров. Суммой матриц
Произведениемматрицы Операциювычитания матриц можно определить следующим способом:
что соответствует вычитанию элементов, стоящих на одинаковых местах. Используя операции сложения и умножения, мы можем находить линейные комбинации матриц, то есть выражения вида Легко проверить, что операции сложения матриц и умножения матрицы на число, называемые линейными операциями, обладают следующими свойствами: 1. 2. 3. 4. 5. 6. 7. 8. Здесь
Транспонирование матрицы. Пусть Транспонированная матрица
Если AT = A то матрицу А называют симметрической, а если АT = -А то кососимметрической. И в том и в другом случае матрицы должны быть квадратными. Свойства транспонированной матрицы: 1) (АT)T = A, 2) (А + B)T = AT + BT. 3) (λA)T = λ + AT. Линейная зависимость строк и столбцов: Строки и столбцы матрицы можно рассматривать как матрицы – строки и матрицы – столбцы, соответственно над ними тоже можно выполнять линейные операции. Ограничение на операцию сложения состоит лишь в том, что строки (столбцы) должны быть одинаковой длины (высоты), но это условие всегда выполняется для строк (столбцов) одной матрицы. Строки (столбцы) a1 … as называют линейно зависимыми, если равенство λ1a1 + … + λ2as =0 Где 0 в правой части – нулевая строка (столбец), возможно лишь при λ1 = … = λs = 0. В противном случае, когда существуют такие действительные числа λ1 … λs, не равные нулю одновременно, что выполняется равенство (λ1a1 + … + λ2as =0), эти строки (столбцы) называют линейно зависимыми. Th1Строки (столбцы) линейно зависимы тогда и только тогда, когда хотя бы одна (один) из них является линейной комбинацией остальных. Док-во: Если строки a1, … as линейно зависимы, то согласно определению линейно независимых строк, существуют такие действительные числа λ1, … λs, не равные нулю одновременно, что λ1a1 + … + λsas = 0. Выберем ненулевой коэффициент λi. Для простоты пусть это будет λ1. Тогда: λ1a1 = (-λ2)a2 + … + (-λs)as, и следовательно a1 = (-λ2/λ1)a2 + … + (-λs/λ1)as, т.е строка a1 представляется в виде линейной комбинации остальных строк. Th.2Пусть строки (столбцы) a1, … as а каждая из строк (столбцов) b1, … bl являются их линейной комбинацией. Тогда все строки (столбцы) a1, … as , b1, … bl линейно зависимы. Док-во. По условию b1 есть линейная комбинация a1, … as т.е b1 = λ1a1 + … + λ2as . В эту линейную комбинацию добавим строки (столбцы) b2 … bl (при l>1) с нулевыми коэффициентами. b1 = λ1a1 + … + λ2as + 0 b2 + … + 0 bl. Согласно Th1 строки (столбцы) a1, … as , b1, … bl линейно зависимы. Определитель есть функция, определенная на множестве квадратных матриц порядка Определитель квадратной матрицы Определителем квадратной матрицы
где Свойства определителей: 1. Определитель не меняется при транспонировании. 2. Если одна из строк определителя состоит из нулей, то определитель равен нулю. 3. Если в определителе переставить две строки, определитель поменяет знак. 4. Определитель, содержащий две одинаковые строки, равен нулю. 5. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k. 6. Определитель, содержащий две пропорциональные строки, равен нулю. 7. Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых ai j = bj + cj (j= 8. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число.
При переходе от матрицы
Это соотношение верно и при
В силу равенства (14.11) получим
По определению алгебраического дополнения получим
Определитель построенной матрицы обозначают Мij и называют минором, соответствующим элементу aij . Число Аij = (-1)i+jМij называют алгебраическим дополнением, соответствующим этому же элементу aij Для квадратной матрицы
Доказательство. Пусть С другой стороны, используя разложение определителя по
где
Так как
Все свойства определителя, сформулированные для строк , справедливы и для столбцов, в частности, справедливо разложение определителя по Определитель треугольной матрицы равен произведению элементов ее главной диагонали. Доказательство. Воспользуемся индукцией по порядку матрицы. Для
утверждение верно. Предположим, что доказываемое утверждение верно для матриц порядка Если
Справа стоит определитель треугольной марицы порядка Если Итак, утверждение верно для матрицы порядка Определитель единичной матрицы равен единице, Определитель n –ого порядка. A = Решение. Разложим определитель А по первой строке: A = a11 A11 = Определитель, стоящий справа, можно снова разложить по первой строке, тогда получим: A = .И так далее. После n шагов придем к равенству A = а11 а22... ann. С помощью элементарных преобразований строк любая матрица приводится к ступенчатому виду. Квадратная матрица ступенчатого вида является частным случаем верхней треугольной матрицы, у которой диагональные элементы, начиная с некоторого, могут быть равны нулю. Определитель такой матрицы считается как определитель треугольной матрицы. Квадратную матрицу Произведением матрицы
где Во-первых, в этом определении нужно обратить внимание на то, что важен порядок сомножителей, нужно знать, какой сомножитель первый, а какой второй. Во-вторых, нужно отметить, что произведение определено только в том случае, если число столбцов первого сомножителя равно числу строк второго. Если это условие не выполняется, то произведение не определено. В-третьих, размеры результата умножения определяются следующим образом: число строк результата равно числу строк первого сомножителя, а число столбцов результата равно числу столбцов второго сомножителя. Правило вычисления элементов произведения можно сформулировать следующим образом:Для того, чтобы вычислить элемент произведения, стоящий в i-ой строке и j-ом столбце, нужно взять Легко проверить, что произведение квадратных матриц одного порядка всегда существует (определено).
Матрица Если матрица Если определитель матрицы равен нулю, то обратная к ней не существует. Если обратная матрица существует, то она единственна. Доказательство. Пусть две матрицы
Следовательно, Обратная матрица для квадратной матрицы Присоединенной матрицей называют матрицу A* , транспонированную к матрице (Aij) алгебраических дополнений. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


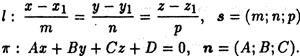











 ;
; 
 делим обе части на а2 (а2 -с2 ). Получили:
делим обе части на а2 (а2 -с2 ). Получили:  Так как а > с, то можно обозначить а2 -с2 = b2 . Получим:
Так как а > с, то можно обозначить а2 -с2 = b2 . Получим: 
 так как 0 < с < а , то 0< ε <1.
так как 0 < с < а , то 0< ε <1.


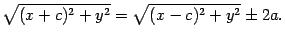
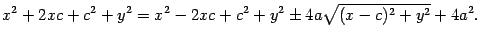

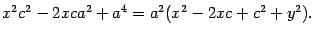
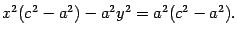
 уравнение принимает вид
уравнение принимает вид 



 Возведем обе части последнего уравнения в квадрат:
Возведем обе части последнего уравнения в квадрат:  откуда
откуда 
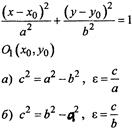








 3)квадратная матрица. Если m=n.У квадратной матрицы выделяют последовательности элементов a11 a 22 … ann - главную диагональ, и an1 an-1,2 … a1n – побочную диагональ. 4)прямоугольная матрица. Если m<>n. 5)Если в квадратной матрице порядка n все элементы кроме главной диагонали равны нулю, то её называют Диагональной матрицей.
3)квадратная матрица. Если m=n.У квадратной матрицы выделяют последовательности элементов a11 a 22 … ann - главную диагональ, и an1 an-1,2 … a1n – побочную диагональ. 4)прямоугольная матрица. Если m<>n. 5)Если в квадратной матрице порядка n все элементы кроме главной диагонали равны нулю, то её называют Диагональной матрицей.
 . Порядок матрицы при этом обычно ясен из контекста. Например,
. Порядок матрицы при этом обычно ясен из контекста. Например, 
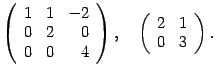
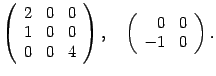
 и
и  размеров
размеров  является матрица
является матрица  таких же размеров, у которой
таких же размеров, у которой  ,
,  ,
,  . Другими словами, при сложении матриц складываются элементы, стоящие на одинаковых местах. Например,
. Другими словами, при сложении матриц складываются элементы, стоящие на одинаковых местах. Например,
 называется матрица
называется матрица  ,
,  ,
,  . Другими словами, при умножении матрицы на число все ее элементы умножаются на это число. Например,
. Другими словами, при умножении матрицы на число все ее элементы умножаются на это число. Например,  .
.
 , где
, где  -- числа,
-- числа,  - матрицы одинаковых размеров.
- матрицы одинаковых размеров. -- свойство коммутативности;
-- свойство коммутативности; -- свойство ассоциативности;
-- свойство ассоциативности; ;
; ;
; -- свойство дистрибутивности;
-- свойство дистрибутивности; ;
; ;
; .
. -- матрицы,
-- матрицы,  -- числа, 0 -- нулевая матрица.
-- числа, 0 -- нулевая матрица. , что
, что  ,
,  ,
,  .
. или
или  . Операция транспонирования заключается в том, что строки и столбцы в исходной матрице меняются ролями. В транспонированной матрице первым столбцом служит первая строка исходной матрицы, вторым столбцом -- вторая строка исходной матрицы и т.д. Например,
. Операция транспонирования заключается в том, что строки и столбцы в исходной матрице меняются ролями. В транспонированной матрице первым столбцом служит первая строка исходной матрицы, вторым столбцом -- вторая строка исходной матрицы и т.д. Например,

 и принимающая значения в множестве чисел.
и принимающая значения в множестве чисел.  или
или  .
. второго порядка называется число
второго порядка называется число  . Определителем квадратной матрицы
. Определителем квадратной матрицы  порядка
порядка  , называется число
, называется число
 -- определитель матрицы порядка
-- определитель матрицы порядка  , полученной из матрицы
, полученной из матрицы  .
. ), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj.
), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj. Доказательство. Если
Доказательство. Если  , положим
, положим  . Пусть
. Пусть  . Тогда
. Тогда 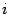 -ую строку поменяем местами со строкой с номером
-ую строку поменяем местами со строкой с номером  . Определитель сменит знак. Затем строку с номером
. Определитель сменит знак. Затем строку с номером  . Определитель снова сменит знак. Процесс перестановки строк будем продолжать до тех пор, пока
. Определитель снова сменит знак. Процесс перестановки строк будем продолжать до тех пор, пока  ). Таким образом
). Таким образом
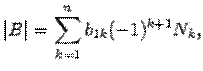 где
где 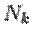 -- определитель матрицы, полученной из матрицы
-- определитель матрицы, полученной из матрицы 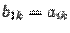 . Результат вычеркивания в матрице
. Результат вычеркивания в матрице  , где
, где  -- определитель матрицы, полученной при вычеркивании в матрице
-- определитель матрицы, полученной при вычеркивании в матрице 

 . Тогда из предыдущего равенства вытекает
. Тогда из предыдущего равенства вытекает что и требовалось доказать.
что и требовалось доказать. выполнено соотношение
выполнено соотношение 
 -ая строка заменена
-ая строка заменена 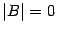 .
.
 -- алгебраическое дополнение к элементу
-- алгебраическое дополнение к элементу  . Так как все строки матрицы
. Так как все строки матрицы  . Так как по построению матрицы
. Так как по построению матрицы  , то
, то
 , то равенство (14.12) доказано.
, то равенство (14.12) доказано. :
:
 ):
):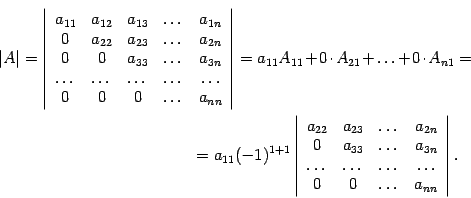
 . Поэтому
. Поэтому  .
. .
.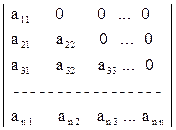 ,в котором все элементы по одну сторону от главной диагонали равны нулю.
,в котором все элементы по одну сторону от главной диагонали равны нулю. .
. , и невырожденной или неособенной матрицей, если
, и невырожденной или неособенной матрицей, если 
 называется матрица
называется матрица  , элементы которой вычисляются по формуле
, элементы которой вычисляются по формуле
 ,
,  .
. Умножение матриц обладает следующими свойствами:
Умножение матриц обладает следующими свойствами: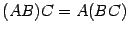 -- ассоциативность умножения;
-- ассоциативность умножения;  , где
, где  -- число;
-- число;  ,
,  -- дистрибутивность умножения;
-- дистрибутивность умножения; 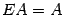 ,
,  , где
, где  .
. .
. и
и 
 .
.