
|
|
Плоскопараллельное движение
Движение тела называется плоскопараллельным или плоским, если тело перемещается так, что траектории всех его точек параллельны какой-то неподвижной плоскости. В качестве типичных примеров можно привести движение шатуна АВ в кривошипно-шатунном механизме или качение без проскальзывания колеса по плоскости или поверхности (рис. 10). Для каждого момента времени и соответствующего ему положения кинематические характеристики движения произвольной точки звена, совершающего плоское движение, можно представить как векторную сумму двух характеристик: поступательного движения этой точки вместе с определенной точкой звена, выбранной за полюс и характеристиками поворота её вокруг полюса. Обычно при решении задач, связанных с определением ускорений (скоростей), за полюс выбирают общую точку рассматриваемого звена и предыдущего, для которого движение задано или уже определено. Последнее позволяет сделать ускорение (скорость) полюса известным (на рисунках, представленных выше, за полюс выгодно взять точку А). В качестве точки, ускорение (скорость) которой необходимо найти, первоначально тоже выбирается общая точка рассматриваемого и последующего звена (точка В).
Рис. 10
Последнее позволяет определить ускорение (скорость) этой точки хотя бы по направлению, что упрощает задачу. Таким образом, всегда можно получить векторные равенства
где
Далее необходимо сделать так, чтобы в уравнениях (7) осталось только две неизвестных, а затем спроецировать их на удобно выбранные оси Х и Y и ,решая полученную систему, определить их значения. Т.е. решение уравнений (7) полностью аналогично аналитическому или графическому решению уравнений (5) для сложного движения точки. Чтобы обеспечить в уравнениях (7) только две неизвестных (это всегда можно сделать), необходимо иметь в виду следующее: вектора Решить задачу с помощью МЦС можно, если известны скорость одной точки (например, А) по величине и направлению, а другой (например, В) по направлению (обычно это общие точки данного звена и смежных с ним звеньев). Это позволяет найти
Рис. 11
Таким образом, если задано движение ведущего звена w1, размеры (длины звеньев
Если необходимо найти скорость любой другой точки звена 2 (например, С), то её необходимо соединить с МЦС и её скорость будет перпендикулярна её радиусу, а равна VC=w2∙P2C. Расстояния (радиусы поворота) от точек звена до МЦС определяются с помощью геометрии на основе заданных размеров и углов. Обычно они находятся из прямоугольных треугольников или из обыкновенных треугольников с применением теорем синусов или косинусов. В частном случае для положения механизма, когда перпендикуляры к скоростям точек А и В будут параллельны. МЦС стремится к бесконечности. Тогда Рассмотрим другие частные случаи определения скоростей через МЦС, связанные с качением колес (последнее справедливо и для делительных окружностей зубчатых колес с движущимися центрами). Если колесо катится (без проскальзывания) по плоской или криволинейной неподвижной поверхности, то МЦС всегда будет в той точке колеса, которая касается этой поверхности (рис. 12).
Рис. 12
Если задано
Аналогично может быть определено и угловое ускорение колеса, если известно aC
Последнее справедливо, т.к. расстояние до МЦС центра колеса при движении не изменяется, т.е. не зависит от времени (для рычажных механизмов последняя формула не применяется). Если поверхность по которой обкатывается колесо сама движется, то для определения положения МЦС колеса необходимо знать скорости двух точек колеса по величине и направлению (обычно это центр колеса С и точка касания движущейся поверхности, например точка В).
Рис. 13
На рис. 13 приведен пример дифференциального механизма, имеющего два ведущих звена (шестерня 1 и рычаг-водило 2) скорости которых w1 и w2 заданы. Промежуточным звеном является шестерня-сателит 3, совершающая плоское движение, а выходным шестерня 4. Если заданы размеры механизма (радиусы или числа зубьев и модуль зацепления) то через МЦС колеса 3 можно определить движение ведомого звена w4 . Для точек А звена 2 и В звена 1, совершающих поворот вокруг неподвижного центра О справедливо VA=w2∙OA и VB=w2∙OB. Эти же точки принадлежат и звену 3, МЦС которого (точка Р3) может быть определен, если соединить концы векторов
где P3A=AB-P3B. Решая последнюю систему уравнений легко определить
Тогда можно найти w3 и далее скорость точки С этого же звена VC=w3∙P3C, а т.к. эта же точка принадлежит звену 4, вращающемуся вокруг неподвижного центра О, то для ведомого звена Если скорости точек А и В будут направлены в одну сторону (рис. 14), то МЦС может оказаться за пределами звена 3. В этом случае для определения его тоже используются подобные треугольники и формула (11), в которой P3A=AB+P3B (рис. 14)
Рис. 14
В частном случае, когда Если в данный момент времени известны касательные ускорения точек А и В, которые обычно находят через угловые ускорения ведущих звеньев Здесь
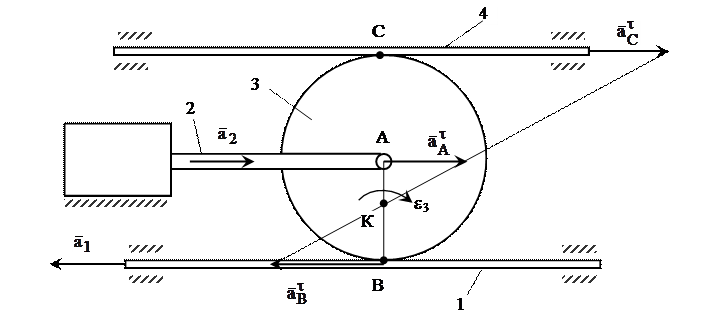
т.е. по заданному движению ведущих звеньев a1, a2 совершающих поступательное движение по прямой, получим aA = a1, aB = a2 и тогда по выше приведенным формулам легко найти e3 и ускорение ведомой зубчатой рейки a4. В заключении рассмотрим на примере определения ускорений точек звеньев, совершающих плоское движение с использованием основной формулы (7) (рис. 16).
Рис. 15
Задача 3. Здесь должно быть задано или заранее определено: положение механизма в данный момент времени (углы j, a, b, g), кинематические характеристики ведущего звена (w1, e1), а также размеры звеньев и положение рассматриваемых точек
Величины нормальных ускорений
Решая эту систему уравнений можно найти значения двух неизвестных Зная w2 и e2 теперь легко найти ускорение любой произвольной точки звена 2, например точки С. Для неё из уравнения (7) следует
где
Теперь проецируем (15) на оси
и по проекциям находим модуль, а если необходимо, то и направление вектора
где g - угол вектора с осью Х. Если в точке С шарнирное соединение с другим звеном CD, совершающим плоскопараллельное движение, то точку С тоже можно взять за полюс и записать
Последнее векторное уравнение решается аналогично уравнению (13). Задача 4. Для колесных механизмов можно взять за полюс центр колеса (например точка А ускорение которой известно) и предварительно определив, как рассмотрено выше (рис. 13, 14 или рис. 15) из подобия треугольников его угловую скорость и угловое ускорение составить для любой точки С колеса, положение которой относительно центра задано, выражение аналогичное (15) (рис. 17)
Рис. 17
или в проекциях на оси
где Теперь используя (17) легко найти ас и g. Таким образом методика решения наиболее сложных задач кинематики, связанных с определением кинематических характеристик точки при сложном движении, а также в случае плоскопараллельного движения сводится к графическому или аналитическому решению векторного уравнения вида (5) или (7). Причем всегда, используя исходные данные задачи, модно сделать так, чтобы в этих уравнениях оказалось только две неизвестных. Обычно это модуль и направление (угол с осью) одного какого-то вектора (см. задачи 1, 3, 4) или модули двух векторов (см. задачи 2, 3). Кроме того, при определении скоростей точек или угловых скоростей звеньев при плоскопараллельном движении наиболее целесообразно использовать МЦС звена (см. рис. 13, 14, 15). Причем общим для всех задач является последовательный переход от одного ведущего звена к последующему ведомому через их общие точки. При этом записываются формулы кинематики для общей точки звеньев, учитывающие вид движения её с одним и другим звеном, а также, что скорость или ускорение общей точки одинаковы в движении с каждым из смежных звеньев. Это и позволяет получить в векторных уравнениях вида 5 или 7 только две неизвестные, а затем спроецировав их на оси координат получить алгебраические уравнения, которые легко решаются и позволяют найти значения неизвестных. Затем найденные характеристики движения общей точки и используются для составления нового векторного уравнения для определения движения следующей общей точки и так далее (см. задачу 3, когда точка С является общей точкой с последующим звеном CD).
Задание №1. Сложное движение точки. Определение абсолютной скорости и абсолютного ускорения точки Точка M движется относительно тела D. По заданным уравнениям относительного движения точки M и движения тела D определить для момента времени t=t1 абсолютную скорость и абсолютное ускорение точки M. Схемы механизмов показаны на рис. 1 – 29, а необходимые для расчета данные помещены в табл. 3.
Таблица 3
Примечания. Для каждого варианта положение точки M на схеме соответствует положительному значению sr; в вариантах 5, 10, 12, 13, 20-24, 28-29 OM = sr – дуга окружности; на схемах 5, 10, 12, 21, 24 OM – дуга, соответствующая меньшему центральному углу. Относительное движение точки M в вариантах 6 и 27 и движение тела D в вариантах 23 определяются уравнениями, приведенными в последнем столбце табл. 3.
Пример выполнения задания Дано: схема механизма (рис. 7),
Решение: Будем считать, что в заданный момент времени плоскость чертежа совпадает с плоскостью Д. Положение точки M на теле Д определяется расстоянием При
Угол
откуда находим значение угла
Абсолютная скорость точки M найдем как геометрическую сумму относительной и переносной скоростей:
Модуль относительной скорости
где
При t = 2 с
Положительный знак у Модуль переносной скорости
где точка M, как и AO участвует в поступательном движении тела Д (т.е. AO всегда параллельна самой себе).
При t = 2 c
Направление Тогда, согласно (1) модуль переносной скорости:
Абсолютное ускорение точки M равно геометрической сумме относительного, переносного и кориолисова ускорений:
или в развернутом виде
Модуль относительного касательного ускорения
При t = 2 c
Знаки Относительное нормальное ускорение
Угловое переносное ускорение находим как
При t = 2 c
Модуль переносного центростремительного ускорения
а модуль переносного вращательного ускорения
При t = 2 c
Модуль кориолисова ускорения
Так как вектор
Покажем направление ускорений точки M в момент времени Модуль абсолютного ускорения точки М находим способом проекций:
После вычисления получаем:
Задание №2. Кинематический анализ плоского механизма Найти для заданного положения механизма скорости и ускорения точек B и C, а также угловую скорость и угловое ускорение звена, которому эти точки принадлежат. Схемы механизмов помещены на рисунках, а необходимые для расчета данные приведены в табл. 2. Таблица 2 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

 , (7)
, (7) - характеристики искомой точки;
- характеристики искомой точки; - характеристики для полюса;
- характеристики для полюса; - характеристики поворота вокруг полюса.
- характеристики поворота вокруг полюса. всегда перпендикулярны радиусу АВ, а вектор
всегда перпендикулярны радиусу АВ, а вектор  направлен по радиусу к центру (полюсу) А и равен
направлен по радиусу к центру (полюсу) А и равен  . При этом, угловая скорость звена wВА, которая для выбранного положения звена не зависит от выбора полюса, может быть определена при решении уравнения для скоростей (7), т.к.
. При этом, угловая скорость звена wВА, которая для выбранного положения звена не зависит от выбора полюса, может быть определена при решении уравнения для скоростей (7), т.к.  , либо чаще через мгновенный центр скоростей (МЦС). МЦС это особый полюс, у которого в данном положении звена собственная скорость равна нулю. Находится он на пересечении перпендикуляров к скоростям двух точек звена, совершающего плоское движение.
, либо чаще через мгновенный центр скоростей (МЦС). МЦС это особый полюс, у которого в данном положении звена собственная скорость равна нулю. Находится он на пересечении перпендикуляров к скоростям двух точек звена, совершающего плоское движение. по величине, а также определить угловую скорость звена, например w2, совершающего плоское движение (рис. 11).
по величине, а также определить угловую скорость звена, например w2, совершающего плоское движение (рис. 11).
 ,
,  и
и  ) и конкретное положение механизма (с помощью углов наклона звеньев с одной из осей), то можно найти
) и конкретное положение механизма (с помощью углов наклона звеньев с одной из осей), то можно найти  (8)
(8) и говорят, что звено 2 совершает мгновенно поступательное движение.
и говорят, что звено 2 совершает мгновенно поступательное движение.
 , радиус колеса R и другие необходимые расстояния и углы, то
, радиус колеса R и другие необходимые расстояния и углы, то (9)
(9) (10)
(10)

 . Положение этой точки на общем перпендикуляре к скоростям теперь находится из подобия треугольников, т.е.
. Положение этой точки на общем перпендикуляре к скоростям теперь находится из подобия треугольников, т.е. (11)
(11)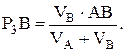 (12)
(12) .
.
 , получим w3 = 0 и скорости всех точек звена в этот момент одинаковы.
, получим w3 = 0 и скорости всех точек звена в этот момент одинаковы. или по заданному движению реек 1 и 2 (рис. 15), то аналогично w3 можно из подобия треугольников найти e3 .
или по заданному движению реек 1 и 2 (рис. 15), то аналогично w3 можно из подобия треугольников найти e3 .
 . Это позволит найти ускорение всех точек звена 2, совершающего плоское движение, а также движение ведомых звеньев (w3, e3, aD). Для этого сначала определяется ускорение общей точки А
. Это позволит найти ускорение всех точек звена 2, совершающего плоское движение, а также движение ведомых звеньев (w3, e3, aD). Для этого сначала определяется ускорение общей точки А  и направление (точнее прямые по которым направлены вектора) ускорений другой общей точки В (учитывается их вращение вокруг неподвижных центров как на рис. 16, либо поступательное движение точки В вместе с ведомым звеном как на рис. 10). Тогда из выражения (7) следует
и направление (точнее прямые по которым направлены вектора) ускорений другой общей точки В (учитывается их вращение вокруг неподвижных центров как на рис. 16, либо поступательное движение точки В вместе с ведомым звеном как на рис. 10). Тогда из выражения (7) следует (13)
(13)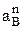 вращения точки В вокруг центра О3 вместе со звеном 3 и
вращения точки В вокруг центра О3 вместе со звеном 3 и  - вращения этой точки вокруг полюса А вместе со звеном 2 найдем, используя значения w2 и w3, которые определяются через МЦС, как было рассмотрено выше в примере (рис. 11), т.е.
- вращения этой точки вокруг полюса А вместе со звеном 2 найдем, используя значения w2 и w3, которые определяются через МЦС, как было рассмотрено выше в примере (рис. 11), т.е.  . Тогда в векторном уравнении (13) остается две неизвестные и его можно спроецировать на оси Х и Y
. Тогда в векторном уравнении (13) остается две неизвестные и его можно спроецировать на оси Х и Y (14)
(14)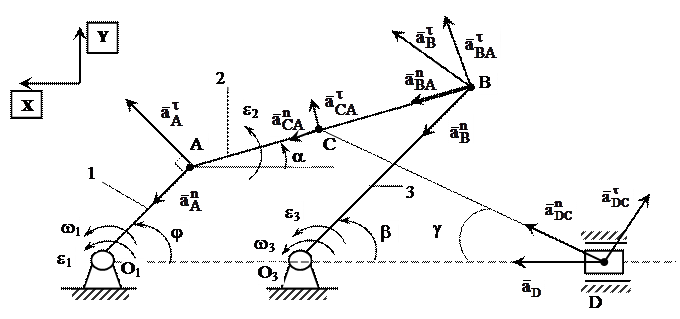 Рис. 16
Рис. 16 , а затем
, а затем 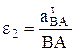 и
и  . Если значение какого-то касательного ускорения окажется отрицательным, это означает, что правильное направление вектора противоположно первоначально выбранному на рис. 16 (соответственно противоположно направлено соответствующее угловое ускорение e2 или e3 ).
. Если значение какого-то касательного ускорения окажется отрицательным, это означает, что правильное направление вектора противоположно первоначально выбранному на рис. 16 (соответственно противоположно направлено соответствующее угловое ускорение e2 или e3 ). (15)
(15)
 (16)
(16) .
. (17)
(17)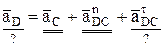 (18)
(18)






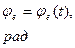

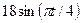










































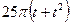




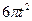
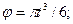
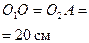

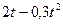
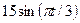


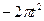

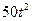





 φe=
φe=  φe=
φe= 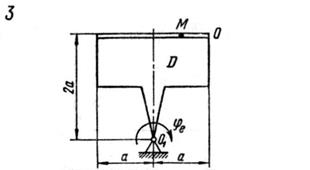 φe=
φe=  φe=
φe=  φe=
φe= 
 φe=
φe=  φe=
φe=  φe=
φe=  φe=
φe=  φe=
φe=  φe=
φe=  φe=
φe=  φe=
φe=  φe=
φe=  φe=
φe=  φe=
φe=  φe=
φe= 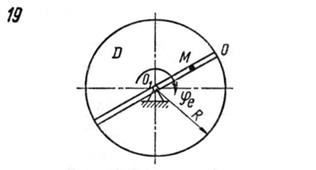 φe=
φe=  φe=
φe=  φe=
φe=  φe=
φe= 
 φe=
φe= 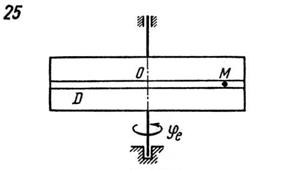 φe=
φe=  φe=
φe= 
 φ=
φ= 
 ,
,  ,
,  ,
,  ,
,  .
. Найти: абсолютные скорость и ускорение
Найти: абсолютные скорость и ускорение  точки М.
точки М. .
. ,
,
 вычисляется из длины дуги ОМ
вычисляется из длины дуги ОМ ,
, .
.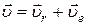 .
.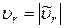 ,
, .
.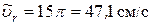 ,
, 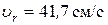 .
. показывает, что вектор
показывает, что вектор  направлен в сторону возрастания
направлен в сторону возрастания 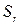 .
. (1)
(1) .
. .
. совпадает с направлением отсчета угла
совпадает с направлением отсчета угла  , следовательно, вектор
, следовательно, вектор 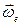 направлен перпендикулярно плоскости чертежа от нас.
направлен перпендикулярно плоскости чертежа от нас.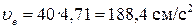 .
. Вектор
Вектор  направлен по касательной к окружности O2A в сторону вращения тела Д. В момент времени t = 2 c положение тела Д таково, что значение угла
направлен по касательной к окружности O2A в сторону вращения тела Д. В момент времени t = 2 c положение тела Д таково, что значение угла  составляет
составляет  рад. Следовательно, вектор
рад. Следовательно, вектор 


 ,
, .
. .
. одинаковы, следовательно, относительное движение точки М ускоренное.
одинаковы, следовательно, относительное движение точки М ускоренное. .
. .
.
 ,
,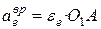 .
. ,
,  .
. .
. и
и  , и тогда
, и тогда
 .
. (рис. 9). вектор
(рис. 9). вектор 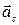 направлен по правилу векторного произведения вдоль направления MА.
направлен по правилу векторного произведения вдоль направления MА. ,
, ,
, .
.