
|
|
Теорема об изменении кинетической энергииМатериальной точки
Данная теорема устанавливает количественную взаимосвязь между работой силы (причиной) и кинетической энергией материальной точки (следствием). Кинетической энергией материальной точки называется скалярная величина, равная половине произведения массы точки на квадрат ее скорости
Кинетическая энергия характеризует то механическое действие силы, которое может превратиться в другие виды энергии, например, в тепловую. Работой силы на данном перемещении называется характеристика того действия силы, которое приводит к изменению модуля скорости. Элементарная работа силы определяется как скалярное произведение вектора силы на элементарный вектор перемещения в точке ее приложения
где Модуль элементарной работы определяется формулой
где a - угол между вектором силы и вектором элементарного перемещения; Полная работа на некотором конечном перемещении определяется интегралом
Из (64) следует, что полная работа может быть вычислена в двух случаях, когда сила постоянная или зависит то перемещения. При F=const получаем При решении задач часто удобно пользоваться аналитическим способом вычисления силы
где Fx, Fy, Fz – проекции силы на координатные оси. Теорема: Изменение кинетической энергии материальной точки на некотором ее перемещении равно работе силы, действующей на точку, на том же перемещении.
Теоремой удобно пользоваться, когда среди заданных и искомых параметров присутствуют масса точки, ее начальная и конечная скорость, силы и перемещение.
Вычисление работы характерных сил. 1. Работа силы тяжести вычисляется как произведение модуля силы на перемещение точки ее приложения по вертикали
При перемещении вверх работа положительная, при перемещении вниз – отрицательная. 2. Работа упругой силы пружины F=-cx равна
где x0 – начальное удлинение (сжатие) пружины; x1 – конечное удлинение (сжатие) пружины. Работа силы тяжести и упругой силы не зависят от траектории перемещения их точек приложения. Такие силы, работа которых не зависит от траектории, называются потенциальными силами. 3. Работа силы трения. Так как сила трения всегда направлена в сторону, противоположную направлению перемещения, то ее работа равна
Работа силы трения всегда отрицательная. Силы, работа которых всегда отрицательна, называются диссипативными.
Мощность
Важнейшей инженерной динамической характеристикой является мощность, определяющая работу, совершаемую силой в единицу времени
Уравнение (69) справедливо для работы, совершаемой равномерно во времени. В общем случае
Динамика механической системы
Основные определения Механической системой называется такая совокупность материальных точек или тел, в которой положение или движение каждой точки (или тела) зависит от положения и движения всех остальных. Любое твердое тело является механической системой. Внешние силы системы ( Внутренние силы системы ( Свойства внутренних сил системы: В соответствии с третьим законом Ньютона геометрическая сумма всех внутренних сил системы всегда равна нулю, аналогично геометрическая сумма моментов всех внутренних сил системы равна нулю.
Центр масс системы – это такая точка, которая определяется уравнением
При решении задач удобно пользоваться аналитическими выражениями для нахождения центра масс
где xC, yC, zC – координаты центра масс системы; xk, yk, zk, mk – координаты и масса каждой точки системы; rC, rk – радиус-вектор, проведенный соответственно в центр масс системы и каждую ее точку. Масса системы определяется как арифметическая сумма масс всех ее точек
Момент инерции механической системы. При изучении произвольного (не поступательного) движения механической системы знание массы системы и ее центра не достаточно. Необходимо знать характер распределения масс. Такая характеристика называется моментом инерции системы. Моментом инерции системы относительно некоторого центра называется сумма произведений масс точек на квадрат их расстояния до данного центра
Чаще в технике используется понятие момента инерции тела относительно оси. Моментом инерции системы относительно оси называется арифметическая сумма произведений масс точек на квадрат их расстояний до одной оси.
Центральным моментом инерции механической системы называется момент инерции относительно любой оси, проходящей через центр масс системы. Значения центральных моментов инерции некоторых простейших однородных тел приводятся в справочниках.
Дифференциальные уравнения движения механической системы
Для каждой материальной точки, входящей в данную систему, на основе второго закона Ньютона можно записать следующие ОУД
где
В общем случае для инженерных задач система дифференциальных уравнений (78) является нелинейной и ее аналитическое решение практически невозможно. Исследование таких систем выполняется численными методами с помощью ЭВМ.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

 . (61)
. (61)
 , (62)
, (62) - элементарное перемещение.
- элементарное перемещение. , (63)
, (63) - проекция вектора силы на касательную.
- проекция вектора силы на касательную. . (64)
. (64) .
. ,
, . (65)
. (65) . (66)
. (66) , (67)
, (67) . (68)
. (68)
 . (69)
. (69) . (70)
. (70) ) – это такие силы, с которыми тела, не входящие в данную систему, действуют на тела системы.
) – это такие силы, с которыми тела, не входящие в данную систему, действуют на тела системы. ) – это силы, с которыми тела данной системы действуют друг на друга.
) – это силы, с которыми тела данной системы действуют друг на друга.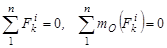 (71)
(71) (72)
(72) , (73)
, (73) . (74)
. (74) . (75)
. (75)
 (76)
(76) Теорема Гюйгенса: Момент инерции тела относительно любой оси, параллельной центральной оси, равен сумме центрального момента инерции и произведения массы системы на квадрат расстояния между осями
Теорема Гюйгенса: Момент инерции тела относительно любой оси, параллельной центральной оси, равен сумме центрального момента инерции и произведения массы системы на квадрат расстояния между осями . (77)
. (77) (78)
(78) - равнодействующая всех внешних сил, приложенных к k-точке;
- равнодействующая всех внешних сил, приложенных к k-точке; - равнодействующая всех внутренних сил приложенных к k-точке.
- равнодействующая всех внутренних сил приложенных к k-точке.