
|
|
Й закон (основной закон динамики)Если равнодействующая всех сил, приложенных к материальной точке, не равна нулю, то эта материальная точка приобретает ускорение, пропорциональное равнодействующей и направленной по ней.
Выражение (47) представляет собой основное уравнение динамики. Й закон (закон равенства действия и противодействия)
Основные задачи динамики
На основе изложенных законов динамики могут быть решены следующие типы задач: 1. Первая (прямая) задача динамики. В этом случае известны характеристики движения точки и по ним, зная массу, на основе уравнения (3) можно найти действующую на тело силу. 2. Вторая (обратная или основная) задача динамики. В этом случае известны действующие на точку (тело) силы и его масса, требуется найти характеристики движения тела, т.е. зависимость от времени его скорости и координат. 3. Общая задача динамики. В этом случае известны некоторые характеристики движения тела, некоторые силы. Требуется определить неизвестные характеристики движения и неизвестные силы. К этому типу задач относятся все инженерные задачи.
Дифференциальные уравнения движения Материальной точки
Основной закон динамики (47) при решении задач проектируют на оси координат.
Декартова система координат. Проектируя (47) на оси, получим
Выражения (48) - дифференциальные уравнения движения в проекции на оси декартовой системы координат где
Естественная система отсчета. Данным способом удобно пользоваться когда известна траектория движения материальной точки.
Из кинематики известно, что
где r - радиус кривизны траектории в точке. Тогда дифференциальные уравнения движения в проекции на естественные оси принимают вид:
Решение второй задачи динамики заключается в двукратном интегрировании уравнений (48) или (49). Для чего необходимо знать начальные условия, т.е. начальную скорость и начальные координаты.
Общие теоремы динамики материальной точки
При решении многих задач можно пользоваться выполненными заранее заготовками, полученными на основе второго закона Ньютона. Такие методы решения задач объединены в этом разделе.
Теорема об изменении количества движения материальной точки
Введем следующие динамические характеристики: 1. Количество движения материальной точки – векторная величина, равная произведению массы точки на вектор ее скорости
2. Импульс силы Элементарный импульс силы – векторная величина, равная произведению вектора силы на элементарный промежуток времени
Тогда полный импульс
При F=const получим S=Ft. Полный импульс за конечный промежуток времени можно вычислить только в двух случаях, когда действующая на точку сила постоянная или зависит то времени. В других случаях необходимо выразить силу как функцию времени. Равенство размерностей импульса (51) и количества движения (50) позволяет установить между ними количественную взаимосвязь. Рассмотрим движение материальной точки M под действием произвольной силы F по произвольной траектории.
Разделяем в (53) переменные и интегрируем
В итоге, принимая во внимание (51), получаем
Уравнение (55) выражает следующую теорему. Теорема: Изменение количества движения материальной точки за некоторый промежуток времени равно импульсу силы, действующей на точку, за тот же интервал времени. При решении задач уравнение (55) необходимо спроектировать на оси координат
Данной теоремой удобно пользоваться, когда среди заданных и неизвестных величин присутствуют масса точки, ее начальная и конечная скорость, силы и время движения. Теорема об изменении момента количества движения Материальной точки
Взаимосвязь между моментом силы (причиной) и моментом количества движения (следствием) устанавливает следующая теорема. Теорема: Производная по времени от вектора момента количества движения материальной точки относительно некоторого центра равна моменту действующей на точку силы относительно того же центра.
При решении задач уравнение (59) необходимо спроектировать на оси координат
В уравнениях (60) моменты количеств движения и силы вычисляются относительно координатных осей. Из (59) вытекает закон сохранения момента количества движения (закон Кеплера). Если момент силы, действующей на материальную точку, относительно какого-либо центра равен нулю, то момент количества движения точки относительно этого центра сохраняет свою величину и направление. Если Теорема и закон сохранения используются в задачах на криволинейное движение, в особенности при действии центральных сил.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
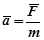 или
или  (47)
(47)
 Две материальные точки действуют друг на друга с силами, лежащими на прямой, соединяющей эти точки, равными по модулю и противоположными по направлению.
Две материальные точки действуют друг на друга с силами, лежащими на прямой, соединяющей эти точки, равными по модулю и противоположными по направлению. 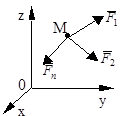
 (48)
(48) - соответственно проекции ускорения на координатные оси Оx, Oy, Oz;
- соответственно проекции ускорения на координатные оси Оx, Oy, Oz; - соответственно суммы проекций сил, действующих на точку на оси координат.
- соответственно суммы проекций сил, действующих на точку на оси координат.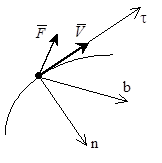 t - касательная, n – главная нормаль, b – бинормаль.
t - касательная, n – главная нормаль, b – бинормаль. ,
, (49)
(49)
 . (50)
. (50)
 . (51)
. (51)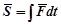 . (52)
. (52) ОУД:
ОУД:  . (53)
. (53) . (54)
. (54) . (55)
. (55) . (56)
. (56) Момент количества движения материальной точки относительно центра равен произведению модуля количества движения точки на плечо, т.е. кратчайшее расстояние (перпендикуляр) от центра до линии, совпадающей с вектором скорости
Момент количества движения материальной точки относительно центра равен произведению модуля количества движения точки на плечо, т.е. кратчайшее расстояние (перпендикуляр) от центра до линии, совпадающей с вектором скорости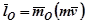 , (57)
, (57) . (58)
. (58) . (59)
. (59) . (60)
. (60) , то
, то  .
.