
|
|
Элементы теории алгоритмов1. Интуитивное понятие алгоритма, вычислимой функции. Ансамбли конструктивных объектов. Область возможных исходных данных. Область применимости алгоритма. Примеры алгоритмов. Вычислимая функция. 2. Модели вычислений. Машины Тьюринга. Машины с неограниченными регистрами (МНР). Тезис Чёрча. 3. Разрешимость, перечислимость подмножества ансамбля конструктивных объектов. Критерий разрешимости перечислимого множества (теорема Поста). Свойства перечислимых, разрешимых множеств. Теорема о графике вычислимой функции. Теорема о проекции. 4. Универсальная вычислимая функция. Невозможность вычислимой функции, универсальной для класса всех всюду определённых вычислимых функций. Главная универсальная вычислимая функция. Теорема о трансляторе (s-m-n-теорема). Примеры неразрешимых проблем. Неразрешимость проблемы остановки. Примеры неразрешимых перечислимых множеств. Многозначная (m-сводимость). Свойства m-сводимости. Теорема Райса о неразрешимости нетривиальных классов в.ф. Примеры применения теоремы Райса. Диофантовы множества. Десятая проблема Гильберта и ее отрицательное решение. [править]Логика высказываний 1. Язык логики высказываний. Логические связки и таблицы истинности. Приведение формул к дизъюнктивной и конъюнктивной нормальным формам. Булевы функции. Полные системы булевых функций. Теорема Поста. Полиномы Жегалкина. 2. Гильбертовский вариант исчисления для логики высказываний. Алфавит, формулы, схемы аксиом и правила вывода исчисления высказываний. Вывод, выводимая формула. Семантическая корректность исчисления высказываний. Вывод из гипотез. Теорема о дедукции для исчисления высказываний. Теорема о семантической полноте исчисления высказываний. 3. Генценовский вариант исчисления для логики высказываний. Понятие секвенциального вывода. Эквивалентность гильбертовского и генценовского вариантов исчисления высказываний. Теорема об устранении сечения. Алгоритм поиска вывода в исчислении высказываний. [править]Логика первого порядка 1. Язык первого порядка. Понятие переменной, предиката, квантора. Сигнатура языка первого порядка, терм, формула. Применение языков первого порядка для описания фрагментов естественных языков. Примеры языков первого порядка: языки теории полей, групп, частичного упорядочения, язык арифметики. 2. Семантика языков первого порядка. Интерпретация языка первого порядка. Выполнимые формулы, общезначимые формулы. Равносильность формул языка первого порядка. Основные равносильности. Предваренные формулы. Приведение формулы к предваренной форме. 3. Исчисление предикатов. Схемы аксиом и правила вывода исчисления предикатов. Вывод из гипотез в исчислении предикатов. Теорема о дедукции для исчисления предикатов. Теорема о корректности исчисления предикатов. Теорема Гёделя о полноте исчисления предикатов. Невозможность аксиоматизации предиката равенства в языке первого порядка. Нормальные модели. Исчисление предикатов с равенством, его корректность и полнота относительно нормальных моделей. Неразрешимость исчисления предикатов. 4. Теории первого порядка. Примеры теорий первого порядка: теория равенства, теория плотного линейного порядка, теория групп, теория полей, арифметика Пеано. Теорема Гёделя о полноте для теорий первого порядка. Теорема Лёвенгейма-Скулема. Теорема компактности для языков первого порядка. Невозможность аксиоматизации свойства конечности в языке первого порядка. Существование счётных нестандартных моделей арифметики. [править]Логика второго порядка 1. Логика 2-го порядка, основные отличия ее от логики 1-го порядка. Определение предиката равенства. Формула, выражающая конечность. Аксиоматизация арифметики. Неперечислимость логики второго порядка. [править]Неклассические логики 1. Интуиционистская логика высказываний. Конструктивное понимание логических связок, семантика Крипке. Аксиомы интуиционистского исчисления высказываний. Теорема о корректности и полноте интуиционистского исчисления высказываний относительно семантики Крипке. Доказательство невыводимости законов исключенного третьего и снятия двойного отрицания в интуиционистском исчислении высказываний. Свойство дизъюнктивности для интуиционистской логики. Невозможность задания интуиционистских связок истинностными таблицами с конечным числом значений. 2. Многозначная логика. 3. Модальная логика. Язык модальной логики. Примеры модальностей в естественном языке. Системы аксиом для логик K, K4, S4, S5, GL, Grz. Семантика Крипке для модального языка. Классы шкал Крипке, соответствующие основным аксиомам логик K, K4, S4, S5, Grz. Полнота K, K4, S4, S5, Grz относительно семантики Крипке. Вложение интуиционистской логики высказываний в S4. 4. Временные операторы, языки временных логик. Логика данной шкалы времени. Примеры временных логик: логики линейного времени, логики ветвящегося времени. Перевод формул языка пропозициональной временной логики на языки классической логики I-го и II-го порядка. Пример неэлементарной временной логики. Разрешимость линейных временных логик. Временные логики и верификация программ. Алгебра логики (алгебра высказываний) — раздел математической логики, в котором изучаются логические операции над высказываниями[1]. Высказывания могут быть истинными, ложными или содержащими истину и ложь в разных соотношениях. Определение Базовыми элементами, которыми оперирует алгебра логики, являются высказывания. Высказывания строятся над множеством {B,
а также константы — логический ноль 0 и логическая единица 1. Дизъю́нкт — пропозициональная формула, являющаяся дизъюнкцией одного или более литералов (например Аксиомы 1. 2. 3. 4. 5. 6. 7. 8. 9. Логические операции Простейшим и наиболее широко применяемым примером такой алгебраической системы является множество B, состоящее всего из двух элементов: B = { Ложь, Истина } Как правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина — с логической единицей, а операции отрицания (НЕ), конъюнкции (И) и дизъюнкции (ИЛИ) определяются в привычном нам понимании. Легко показать, что на данном множестве B можно задать четыре унарные и шестнадцать бинарных отношений и все они могут быть получены через суперпозицию трёх выбранных операций. Опираясь на этот математический инструментарий, логика высказываний изучает высказывания и предикаты. Также вводятся дополнительные операции, такие как эквивалентность Логика высказываний послужила основным математическим инструментом при создании компьютеров. Она легко преобразуется в битовую логику: истинность высказывания обозначается одним битом (0 — ЛОЖЬ, 1 — ИСТИНА); тогда операция Впоследствии булева алгебра была обобщена от логики высказываний путём введения характерных для логики высказываний аксиом. Это позволило рассматривать, например, логику кубитов, тройственную логику (когда есть три варианта истинности высказывания: «истина», «ложь» и «не определено») и др. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
, 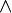 ,
,  , 0, 1}, где B — непустое множество, над элементами которого определены три операции:
, 0, 1}, где B — непустое множество, над элементами которого определены три операции: ). Конъюнкт — пропозициональная формула, являющаяся конъюнкцией одного или более литералов (например
). Конъюнкт — пропозициональная формула, являющаяся конъюнкцией одного или более литералов (например  ).
). ,
, 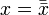
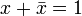

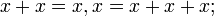
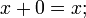
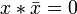

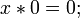

 («тогда и только тогда, когда»), импликация
(«тогда и только тогда, когда»), импликация  («следовательно»), сложение по модулю два
(«следовательно»), сложение по модулю два 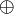 («исключающее или»), штрих Шеффера
(«исключающее или»), штрих Шеффера 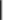 , стрелка Пирса
, стрелка Пирса 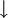 и другие.
и другие.