
|
|
Глава 4. ОДНОМЕРНАЯ ОПТИМИЗАЦИЯ
Методы исключения интервалов
До этого рассматривался вопрос анализа «в статике», который заключается в том, чтобы определить, является ли данное решение оптимальным. Для этого были построены необходимые и достаточные условия оптимальности решения. Далее мы переходим к изучению вопроса анализа «в динамике», связанного с нахождением оптимального решения. С этой целью ниже рассматривается ряд одномерных методов поиска, ориентированных на нахождение точки оптимума внутри заданного интервала. Методы поиска, которые позволяют определить оптимум функции одной переменной путем последовательного исключения подынтервалов и, следовательно, путем уменьшения интервала поиска, носят название методов исключения интервалов. Ранее было дано определение унимодальной функции. Унимодальность функций является исключительно важным свойством. Фактически все одномерные методы поиска, используемые на практике, основаны на предположении, что исследуемая функция в допустимой области, по крайней мере, обладает свойством унимодальности. Полезность этого свойства определяется тем фактом, что для унимодальной функции f(x) сравнение значений f(x) в двух различных точках интервала поиска позволяет определить, в каком из заданных двумя указанными точками подынтервалов точка оптимума отсутствует.
1) Если f(x1) > f(x2), то точка минимума f(x) не лежит в интервале (а, х1), т.е. 2) Если f(x1) < f(x2), то точка минимума не лежит в интервале (х2, b), т.е. Замечание. Если f(x1) = f(x2), то можно исключить оба крайних интервала (а, х1) и (х2, b); при этом точка минимума должна находится в интервале (х1, х2). Согласно приведенной выше теореме, которую иногда называют правилом исключения интервалов, можно реализовать процедуру поиска, позволяющую найти точку оптимума путем последовательного исключения частей исходного ограниченного интервала. Поиск завершается, когда оставшийся подынтервал уменьшается до достаточно малых размеров. Заметим, что правило исключения интервалов, устраняет необходимость полного перебора всех допустимых точек. Несомненным достоинством поисковых методов такого рода является то, что они основаны лишь на вычислении значений функций. При этом не требуется, чтобы исследуемые функции были дифференцируемы; более того, допустимы случаи, когда функцию нельзя даже записать в аналитическом виде. Единственным требованием является возможность определения значений функции f(x) в заданных точках x с помощью прямых расчетов или имитационных экспериментов. Вообще в процессе применения рассматриваемых методов поиска можно выделить два этапа: · этап установления границ интервала, на котором реализуется процедура поиска границ достаточно широкого интервала, содержащего точку оптимума; · этап уменьшения интервала, на котором реализуется конечная последовательность преобразований исходного интервала с тем, чтобы уменьшить его длину до заранее установленной величины. В данном разделе рассматриваются методы решения одномерных задач оптимизации вида где х – скаляр, a и b – соответственно концы интервала, из которого берутся значения переменной х. В основном рассматриваются алгоритмы, связанные с построением улучшающей последовательности. Решением задачи называется х*, при котором f(x*) ³ f(x) для любого значения
Метод сканирования
Достоинство метода в том, что можно найти глобальный максимум критерия, если f(x) – многоэкстремальная функция. К недостаткам данного метода относится значительное число повторных вычислений f(x), что в случае сложной функции f(x) требует существенных затрат времени. На практике можно реализовать одну из основных модификаций метода – последовательное уточнение решения, или сканирование с переменным шагом (рис. 16). Рассмотрим иллюстрацию модифицированного метода сканирования: 1 – интервал, включающий в себя искомый максимум функции после первого этапа сканирования (исходный участок разбит на 5 участков); 2 – то же после второго этапа. На первом этапе сканирование осуществляют с крупным шагом, затем отрезок, внутри которого получено наибольшее значение f(х), разбивается на более мелкие отрезки, ищется новый отрезок, внутри которого уточненное значение максимума. Он (новый отрезок) опять делится на более мелкие и т. д., тех пор, пока величина отрезка, содержащего максимальное значение f(x), не будет меньше заданной погрешности. Главный недостаток этого варианта метода – возможность пропуска «острого» глобального максимума f(x). Пример 11. Найти минимальное значение f* и точку минимума х* функции f(x)=x4+8x3-6x2-72х на отрезке [1.5; 2]. Точку х* найти с погрешностью e=0,05. Решение. Будем разбивать первоначальный и новый, удовлетворяющий нас, интервал на 4 части, при этом новый шаг рассчитываем по формуле: где n – количество частей деления интервала, ai, bi – концы интервала, в котором содержится максимальное значение функции, погрешность Таблица 3
Продолжение табл. 3
Итак, Пример 12. Найти точку минимума х* функции Решение. Будем разбивать первоначальный и новый, удовлетворяющий нас, интервал на 4 части. Таблица 4
Итак, Пример 13. Дана функция f(x) = sin (x+1). Найти максимум на интервале [-1; 2] с точностью e=0,05. Решение. Будем разбивать первоначальный и новый, удовлетворяющий нас, интервал на 4 части, при этом новый шаг рассчитываем по формуле: где n – количество частей деления интервала, ai, bi – концы интервала, в котором содержится максимальное значение функции, погрешность Таблица 5
Продолжение табл. 5
Итак,

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

 , а её минимум достигается в точке х*. Рассмотрим точки х1 и х2, расположенные в интервале таким образом, что a < x1 < x2 < b. Сравнивая значения функции в точках х1 и х2, можно сделать следующие выводы:
, а её минимум достигается в точке х*. Рассмотрим точки х1 и х2, расположенные в интервале таким образом, что a < x1 < x2 < b. Сравнивая значения функции в точках х1 и х2, можно сделать следующие выводы: (см. рис. 14).
(см. рис. 14). (см. рис. 15).
(см. рис. 15).
 Метод заключается в последовательном переборе всех значений
Метод заключается в последовательном переборе всех значений 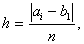
 , где i - номер итерации.
, где i - номер итерации.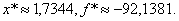
 на отрезке [0.5; 1] с точностью e=0,05.
на отрезке [0.5; 1] с точностью e=0,05.
