
|
|
Выпуклость, вогнутость функцииОпределение. График функцииf(x) называется выпуклым(рис. 9)на интервале (a, b) (вогнутым (рис. 10) на интервале (b, с)), если все точки графика расположены ниже (выше) любой его касательной на этом интервале. Теорема 1. Если функция f(x) дважды дифференцируема на интервале и во всех его точках Определение. Точкой перегиба графика функции называется точка этого графика, которая отделяет выпуклую его часть от вогнутой (рис. 11).
Теорема 3. Если вторая производная функции в точке b равна нулю Алгоритм определения точек перегиба: Шаг 1. Найти Шаг 2. Определить знак Пример 6. Определить направление выпуклости и точки перегиба кривой Решение. Ищем точки х, в которых Исследуем найденные точки, определяя знак второй производной слева и справа от каждой из них. Запишем это исследование в табл. 2: Таблица 2
Из табл. 2 следует, что х = 1 есть абсцисса точки перегиба кривой: у(1) = 2. Поскольку эта кривая непрерывная, то во всем интервале (-¥, 1) она выпукла, а во всем интервале (1, +¥) – вогнута. Исходя, из определения унимодальной функции и направления выпуклости функции можно утверждать, что: 1) если унимодальная функция выпукла, то она имеет глобальный максимум; 2) если унимодальная функция вогнута, то она имеет глобальный минимум.
Критерий оптимальности
При анализе задач возникают два общих вопроса: 1) Вопрос анализа в «статике». Как определить, представляет ли данная точка х* оптимальное решение задачи? 2) Вопрос анализа в «динамике». Если х* не является точкой оптимума, то какая последовательность действий приводит к получению оптимального решения? В этом разделе основное внимание уделяется решению вопроса анализа «в статике», а именно построению множества критериев оптимальности, позволяющих определить, является ли данное решение оптимальным. Определение. Функция f(x), определенная на множестве S, достигает своего глобального минимума в точке х**ÎS в том и только в том случае, если f(x**) £ f(x) для всех х Î S. Определение. Функция f(x), определенная на множестве S, имеет локальный минимум в точке х* Î S в том и только в том случае, если f(x*) £ f(x) для всех х, удаленных от х* на расстояние, меньшее e, то есть если существует e>0 такое, что для любых х, удовлетворяющих условию /х-х*/<e, выполняется неравенство f(x*) £ f(x). Пример 7. Рассмотрим график некоторой функции y = f(x) (рис. 12). Тогда имеем: х1 – точка локального максимума; х2 – точка локального минимума; х3 – точка глобального максимума; х4 – точка глобального минимума.
Замечание. 1) Всякая точка глобального минимума является и точкой локального минимума этой функции. Обратное, вообще говоря, неверно. 2) Аналогичные определения глобального максимума и локального максимума можно получить путем замены знака неравенства на противоположный. 3) Если функция обладает свойством унимодальности, то локальный минимум автоматически является глобальным минимумом. 4) Если функция не является унимодальной, то возможно наличие нескольких локальных оптимумов, при этом глобальный минимум можно определить путем нахождения всех локальных оптимумов и выбора наименьшего из них.
Идентификация оптимумов
Теорема 1. Необходимые условия того, что х* является точкой локального минимума (максимума) дважды дифференцируемой функции f на открытом интервале (a,b), выражаются следующими соотношениями: Эти условия необходимы, но не достаточны для того, чтобы точка х* была точкой локального минимума (максимума). Определение. Стационарной точкой называется точка х*, в которой если стационарная точка не соответствует локальному оптимуму (минимуму или максимуму), то она является точкой перегиба или седловой точкой. Теорема 2. Пусть в точке х* первые (n-1) производные функции обращаются в нуль, а производная порядка n отлична от нуля. Тогда: 1) если n – нечетное, то х* - точка перегиба; 2) если n – четное, то х* - точка локального оптимума. Кроме того, a) если эта производная положительная, то х* - точка локального минимума; б) если эта производная отрицательная, то х* - точка локального максимума.
Пример 8. Рассмотрим функцию
Эта функция непрерывна во всех точках действительной оси, но недифференцируема при х=2. Функция достигает максимума в точке х=2, которая не является стационарной в соответствии с данным выше определением. Это подтверждает тот факт, что теорема 1 является необходимым, но не достаточным условием оптимума. Пример 9. Найти и идентифицировать оптимумы функции Решение. Найдем первую производную функции: Найдем стационарные точки. Для этого решим уравнение Для идентификации точки оптимума, вычислим значение второй производной в стационарной точке.
Значит, х=0 – точка минимума. Пример 10. Найти и идентифицировать оптимумы функции Решение. Сначала найдем первую производную функции: Найдем стационарные точки. Для этого решим уравнение: Следовательно, стационарные точки: Найдем вторую производную Для идентификации точек оптимума, вычислим значение второй производной в стационарных точках.
Значит, х=1 х=3 – точки локальных минимумов, х=2 – точка локального максимума. Чтобы идентифицировать точку х=0, найдем и вычислим третью производную: Так как
Вопросы к главе 3 1. Приведите определение функции. 2. Что такое область определения и область допустимых значений функции? 3. Какие существуют способы задания функции? Приведите конкретные примеры каждого способа. 4. Дайте определения возрастания и убывания функции. Приведите примеры возрастающей и убывающей функций. 5. Как проверить, является ли функция возрастающей или убывающей? 1. Приведите пример функции, описывающей зависимость предложения от цены. Постройте ее график. 2. Что такое точка перегиба и как её идентифицировать? 3. Как проверить, является ли функция выпуклой или вогнутой? 4. В чем состоит свойство унимодальности функций? 5. Пусть данная точка удовлетворяет достаточным условиям существования локального минимума. Как установить, является ли этот минимум глобальным? 6. Приведите алгоритм определения глобального оптимума.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
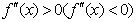 , то ее график вогнут (выпуклый) на этом интервале.
, то ее график вогнут (выпуклый) на этом интервале.
 ,то точка b – точка перегиба графика функции.
,то точка b – точка перегиба графика функции.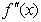 и точки х, в которых
и точки х, в которых  или не существует, а график функции f(x) непрерывен и которые лежат внутри области его расположения.
или не существует, а график функции f(x) непрерывен и которые лежат внутри области его расположения.
 или не существует, а кривая непрерывна и которые лежат внутри области расположения кривой:
или не существует, а кривая непрерывна и которые лежат внутри области расположения кривой:
 существует всюду.
существует всюду.

 ,
, Замечание. Выше предполагалось, что рассматриваемая функция дифференцируема или, что её первая производная существует и непрерывна. Однако если функция не является дифференцируемой, во всех точках области определения, то даже необходимое условие наличия оптимума, позволяющее идентифицировать стационарные точки, может не выполняться в точке оптимума.
Замечание. Выше предполагалось, что рассматриваемая функция дифференцируема или, что её первая производная существует и непрерывна. Однако если функция не является дифференцируемой, во всех точках области определения, то даже необходимое условие наличия оптимума, позволяющее идентифицировать стационарные точки, может не выполняться в точке оптимума.


 Следовательно, получили единственную стационарную точку х=0. Найдем вторую производную
Следовательно, получили единственную стационарную точку х=0. Найдем вторую производную 
 х
х
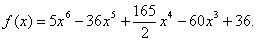
 .
.



 и n=3 – нечетное, то (по теореме 2) х*=0 – точка перегиба.
и n=3 – нечетное, то (по теореме 2) х*=0 – точка перегиба.