
|
|
Методы оптимальных решенийМетодические указания по выполнению контрольной работы Методы оптимальных решенийОглавление. 1 Оглавление. 2 Решение задач ЛП геометрическим методом.. 3 Симплекс-метод решения задач ЛП, обладающих очевидным начальным базисом.. 10 Симплекс-метод решения задач ЛП, обладающих очевидным начальным базисом и заданных в каноническом виде. 14 Решение задач ЛП не обладающих очевидным начальным базисом двухэтапным симплекс-методом.. 15 Экономическая интерпретация алгоритма симплекс-метода и оптимальной симплекс-таблицы.. 19 Транспортная задача линейного программирования. 23 Модели сетевого планирования и управления. 32 Библиографический список. 37 Приложение. 38
Задача 1. Фабрика может изготавливать 2 вида красок: для внутренних работ E и для внешних работ I. Для их производства используются 2 вида исходных материалов: А и В. Максимальные суточные запасы этих материалов равны соответственно 6 т. и 8 т. Расход материалов А и В в расчете на 1 ед. продукции А и В задается следующей таблицей 1. Таблица 1.
Изучение рынка сбыта подсказало следующие закономерности: 1. суточный спрос на краску I не превосходит спроса краски E более чем на 1 т.; 2. спрос на краску I не превышает 2 т. в сутки; 3. цена реализации, сложившаяся на рынке, составляет 3000 руб/т для краски Е и 2000 руб/т для краски I. Требуется определить величины суточных объемов производства красок E и I, исходя из имеющихся запасов материалов, ограничений спроса и известных цен реализации с целью получения максимальной прибыли от реализации. Решение. Пусть Тогда математическая модель задачи представляется в виде функции:
и дополнительных условий: конечности запасов исходных материалов:
ограничений на спрос на краски:
и неотрицательности объёмов производства (чтобы задача имела экономический смысл):
Выражение (1) называется целевой функцией, неравенства (2), (3) - ограничениями задачи, а (4) - условиями неотрицательности переменных 1) Заменяем в ограничении знак неравенства на «=» и строим граничную прямую. Для определения искомой полуплоскости, выбираем пробную точку (любую точку, не принадлежащую граничной прямой) и подставляем её координаты в ограничение. Если получаем верное неравенство, то пробная точка принадлежит полуплоскости, иначе – не принадлежит. а)
Пусть О(0,0) – пробная точка (О(0,0) Аналогично определяем полуплоскости для остальных ограничений. б)
О(0,0) – пробная точка: в)
О(0,0) – пробная точка: г) О(0,0) – пробная точка: д) О(0,0) в качестве пробной точки брать нельзя, т.к. е) Q(1,2)-пробная точка: 2) Пересекаясь полуплоскости, образуют многоугольник решений (смотрите рисунок 1). Каждая точка многоугольника решений определяет некоторый план производства, который удовлетворяет всем экономическим и техническим ограничениям. Мы должны из этого множества планов выбрать оптимальный, т.е. план, дающий наибольшую прибыль. Если многоугольника решений нет, то задача несовместна.
Рис. 1. Многоугольник решений при решении задачи ЛПгеометрическим методом 3) Приравниваем целевую функцию Z к нулю и строим линию нулевой прибыли:
4) Строим вектор 5) Перемещаем прямую

Рис. 2. Решение задачи о лакокрасочной фабрике геометрическим методом
6) Определяем координаты точки max (min) и определяем значение Z. Определим координаты точки С:
Тогда Таким образом, максимальная прибыль в размере Возможные случаи при решении задач ЛП 1)Многоугольник решений ограниченная область:
Рис. 3. Задача имеет единственное решение:
Рис. 4. Задача имеет бесконечное число решений: Из рис. 4 видно, что Z0 параллельно отрезку CD, поэтому при нахождении Zmax каждая точка этого отрезка является решением (разные планы производства, дающие одинаковую максимальную прибыль). 2) Многоугольник представляет собой неограниченную многоугольную область:
Рис. 5. Целевая функция не ограничена ни сверху, ни снизу: Zmax=
Рис. 6. Целевая функция ограничена сверху, но не ограничена снизу:
Рис. 7. Целевая функция не ограничена сверху, но ограничена снизу:
Рис.8. Целевая функция ограничена и сверху и снизу:
3) Нет многоугольника решений (задача несовместна): Полуплоскости, ограниченные прямыми Из рис.9 видно, что при добавлении ограничения
Рис 9. Решение геометрическим методом несовместной задачи 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
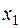 и
и 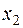 предполагаемые объемы производства красок Е и I соответственно,
предполагаемые объемы производства красок Е и I соответственно,  - соответствующую прибыль.
- соответствующую прибыль. (1)
(1) (2)
(2) (3)
(3) ,
,  . (4)
. (4) . Это ограничение определяет полуплоскость с граничной прямой
. Это ограничение определяет полуплоскость с граничной прямой  :
:  . Для ее построения найдем две ее точки пересечения с осями координат:
. Для ее построения найдем две ее точки пересечения с осями координат:

 :
:  (в), следовательно, пробная точка принадлежит искомой полуплоскости.
(в), следовательно, пробная точка принадлежит искомой полуплоскости. .
.  :
:  .
.
 (в).
(в). .
.  :
:  .
.
 (в).
(в). .
.  :
:  .
. (в).
(в). :
:  (ось OX2).
(ось OX2). . Пусть Q(1,2)-пробная точка:
. Пусть Q(1,2)-пробная точка:  (в).
(в). .
.  (ось OX1).
(ось OX1).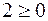 (в).
(в).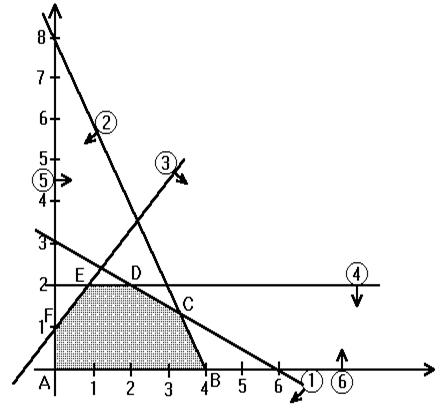
 :
: 

 (коэффициенты при неизвестных в Z
(коэффициенты при неизвестных в Z  ).
). в направлении
в направлении  для поиска max (-
для поиска max (- 
 .
. :
: 
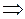
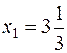 ,
,  .
. .
. тыс. руб. будет получена, если в сутки будет производиться
тыс. руб. будет получена, если в сутки будет производиться  т. краски Е и
т. краски Е и  т. краски I.
т. краски I.



 , Zmin=
, Zmin=  .
.

 .
.



 образуют многоугольник решений.
образуют многоугольник решений. полуплоскости не имеют ни одной общей точки, следовательно, наложенные ограничения несовместны.
полуплоскости не имеют ни одной общей точки, следовательно, наложенные ограничения несовместны.