
|
|
Исследование функции на выпуклость, вогнутость. Точки перегиба графика функции.Возрастание и убывание функции Определение: функция y=f(x) называется неубывающей на [a,b] (невозрастающей) если для любых x1,x2 принадлежащих [a,b] , таких что x1<x2 будет выполняться f(x1)≤f(x2)) ( f(x1) ≥ f(x2) ) Определение: функция y=f(x) называется убывающей на [a,b] (возрастающей) если для любых x1,x2 принадлежащих [a,b] , таких что x1<x2 будет выполняться f(x1)>f(x2)) ( f(x1) < f(x2) ) Только возрастающая и убывающая функции являются монотонными Теорема: для того, чтобы дифференцируемая на интервале (a,b) функция y=f(x) неубывала на (a,b) (невозрастала) необходимо и достаточно: f ' (x)≥0 для любого x из (a,b) ( f ' (x)≤0 для любого x из (a,b)).
Замечание: Условия теоремы для возрастающей и убывающей функций являются только достаточными, но не необходимыми, т.е. если f '(x) > 0 для любого x1,x2 из интервала (a,b), то функция y = f(x) возрастает на интервале (a,b) если f ' (x)<0 для любого x1,x2 из интервала (a,b), то функция y = f(x) убывает на интервале (a,b)
Геометрический смысл: касательная к графику неубывающей на (a,b) функции составляет острый угол с осью Ox (k кас=f ' (x)≥0). Касательная к графику невозрастающей на (a,b) функции образует тупой угол с осью Ox. Если функция f(x) на (a,b) постоянна, то очевидно, что f'(x)=0, а касательная на всём интервале параллельна ось Ox.
Две параллельные прямые на графиках – это касательные Изогнутая линия – график функции y=f(x) Экстремумы функции.
Особую роль в исследовании поведения функции на множестве играют точки, разделяющие интервалы возрастания и убывания функции.
Везде далее будем считать, что y=f(x) непрерывна на [a,b]. Определение:точка x0 называется точкой локального максимума (минимума) функции y=f(x), если существует такая δ -окрестность т. x0, что для всех x Є (x0 - δ; x0+ δ) за исключением x0 выполняется неравенство f(x)<f(x0) (для минимума f(x)>f(x0) ) и записывается
При этом очевидно, что x0-внутренняя точка (a;b), т.е. x0Є(a;b). Максимум и минимум функции называются ее экстремумами. Теорема: необходимое условие существование экстремума: Если в точке x0 функция y=f(x) достигает экстремума, то ее производная в этой точке или равна нулю, или не существует.
В точках экстремумов функции y=f(x) касательная к ее графику или параллельна оси OX, когда существует f '(x0)=0, или перпендикулярна оси OX, когда f '(x0) не существует Точки, в которых производная y=f(x) не существует или равна нулю называют критическими точками. В частном случае, когда f ' (x)=0 критические точки называются стационарными. Замечание: не всякая критическая точка функции y= f(x) является точкой ее локального экстремума. Этот момент поясняют следующие теоремы. Теорема 1: Первое достаточное условие существование экстремума. Точка x0 - критическая точка непрерывной функции y=f(x) является точкой ее экстремума, если при переходе через x0 функция f ' (x) меняет знак. При этом если знак производной меняется с "+" на "-", то точка x0 - точка локального максимума, если с "-" на "+", то точка x0 - точка локального минимума. Если смены знаков производной не происходит, то x0 не является точкой экстремума.
Теорема 2: Второй достаточный признак существования экстремума. Стационарная точка x0 функции y=f(x) дважды дифференцируемой в δ -окрестности точки x0 является точкой ее локального минимума (максимума), если f '' (x0)>0 ( f ''(x0)<0 ).
Абсолютными (глобальными ) экстремумами функции y=f(x) на [a;b] является её наибольшее и наименьшее значение на этом отрезке. Если x1,x2,...xn - критические точки непрерывной функции y=f(x), принадлежащие [a;b], то абсолютные экстремумы обозначаются и находятся следующим образом:
max f(x)= max { f(a) ; f(b) ; f(x1) ; f(x2) ... f(xn)}.
min f(x)= min {f(a) ; f(b) ; f(x1) ; f(x2) ... f(xn)}.
Исследование функции на выпуклость, вогнутость. Точки перегиба графика функции. График дифференцируемой функции y=f(x) называется выпуклым на (a;b), если дуга кривой этого графика для любых x из (a;b) расположена ниже любой касательной, проведенной к графику функции. График дифференцируемой функции y=f(x) называется вогнутым на (a;b), если дуга кривой этого графика для любых x из (a;b) расположена выше любой касательной, проведенной к графику функции.
Выпуклость Вогнутость
Точка M( x0 ; f (x0) ) графика дифференцируемой функции y=f(x), в которой направление выпуклости меняется на противоположное, называется точкой перегиба.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
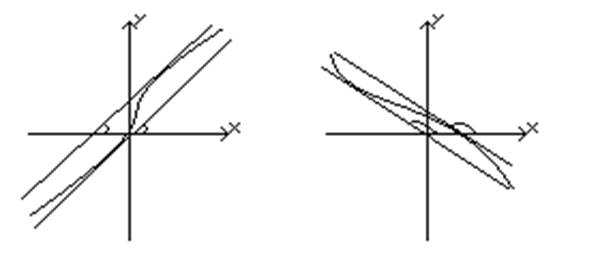



 График дифференцируемой функции лежит по обе стороны касательной, проведенной в точке перегиба.
График дифференцируемой функции лежит по обе стороны касательной, проведенной в точке перегиба.
