
|
|
Под правилами вывода понимаются правила логики без каких-либо ссылок на наглядность и опыт.Сущность понятия доказательства. Методы доказательства теорем. В современном понимании о строгом доказательстве можно говорить в рамках формализованной системы, которая ограничивается не только перечнем неопределяемых понятий и описывающих их аксиом, но и используемыми правилами вывода. Тогда понятие «доказать логическим путем» в рамках такой теории приобретает конкретный смысл. В школьном курсе математики таких жестких правил нет, и используется так называемая «логика здравого смысла». В некоторых случаях учителя считают возможным специально знакомить учащихся с отдельными правилами вывода на соответствующих примерах. Под доказательством теоремы Т будем понимать конечную последовательность предложений ( а) каждое предложение этой последовательности представляет собой аксиому, определение или ранее уже доказанную теорему, или допущение (условие доказываемой теоремы) или же получается из предшествующих предложений по одному из допустимых правил вывода; б) последнее предложение этой последовательности ( Под правилами вывода понимаются правила логики без каких-либо ссылок на наглядность и опыт. Предложение Т является теоремой, если для него может быть построено хотя бы одно доказательство, то есть найдется хотя бы одна последовательность предложений, удовлетворяющая условиям а и б. Доказательство в математике проводится по правилам логики; в основе его лежит дедуктивный вывод. Умозаключение, между посылками и заключением которого имеют место отношения логического следования, называется дедуктивным. Например, число а Имеется большое многообразие дедуктивных рассуждений – правил вывода (дедуктивных умозаключений), используемых (неявно) в математических доказательствах. Назовем несколько широко применяемых правил вывода, которые используются при дедуктивных умозаключениях: 1) Правило заключения: 2) Правило отрицания: 3) Правило силлогизма: 4) Правило контрапозиции: Использование этих правил гарантирует, что умозаключение правильное. Индуктивные выводы характерны тем, что для них нельзя установить таких общих правил. При одной и той же структуре посылок и вывода в зависимости от содержания посылок вывод может быть как истинным так и ложным. Методы доказательства, используемые в школьном курсе математики, можно выделить по двум основаниям: - по способу построения цепочки рассуждений (прямое и косвенное); - по математическому аппарату, используемому в доказательстве. Прямое доказательство теоремы основывается на каком-нибудь несомненном начале, из которого непосредственно устанавливается истинность теоремы. К прямым доказательствам относятся доказательства методами: синтетическим, аналитическим и методом математической индукции. Синтетический метод доказательства теорем характеризуется тем, что при построении цепочки рассуждений на его основе мысль движется «от условия теоремы к ее заключению», то есть от уже установленных предложений данной области к новому доказываемому. К достоинствам синтетического метода доказательства относятся: исчерпывающая полнота, сжатость, краткость. Обычно он применяется при изложении уже разработанных математических теорий, известных доказательств или доказательств, отыскание которых не вызывает у учащихся затруднений. Синтетический метод в методическом отношении имеет и свои недостатки. Остается неясным, как можно обнаружить такое доказательство, почему в рассуждениях поступают так, а не иначе; дополнительные построения никак не аргументируются; учащиеся не привлекаются к доказательству, так как они не представляют, в каком направлении должны протекать дальнейшие рассуждения. Для аналитического метода доказательства характерно обратное движение мысли «от заключения теоремы к ее условию», то есть от доказываемого предложения к тем предложениям (аксиомам, определениям, ранее доказанным теоремам), из которых оно выводится. Преобразование заключения суждения могут быть в форме: а) отыскание достаточных оснований справедливости заключения (восходящий анализ); б) отыскание необходимых признаков справедливости суждения с последующей проверкой обратимости рассуждений (нисходящий анализ). Важнейшим преимуществом аналитического метода является тоя, что учащиеся могут сами сознательно осуществлять поиск доказательства, однако на это требуется достаточно много времени. Обычно при доказательстве теоремы осуществляется последовательное преобразование то условия, то заключения суждения, то есть аналитико-синтетический метод. В основу метода математической индукции положена аксиома арифметики натуральных чисел (приведите примеры доказательства теоремы методом математической индукции). Доказательство, которое основывается на установлении истинности посредством опровержения некоторых суждений, не содержащихся в данной теореме, называется косвенным доказательством теоремы. К косвенным приемам поиска доказательствотносят: • метод «от противного» (истинность доказываемого тезиса устанавливается посредством опровержения противоречащего ему суждения); • разделительный метод, или метод разделения условий (тезис рассматривается как один из возможных вариантов предположений, когда все предположения отвергаются, кроме одного), иначе этот метод называют методом исключения. Для метода доказательства от противного характерно следующее. Пусть надо доказать теорему По-другому это можно сказать так: в качестве допущения принимают отрицание доказываемого предложения и ведут доказательство до получения противоречия. Затем говорят, что «полученное противоречие доказывает теорему». Выражение «противоречие доказывает теорему» можно разъяснить следующим образом: так как противоречие (ложное заключение) получено в результате применения допустимых правил вывода (правильных рассуждений), хотя бы одна из посылок должна быть ложной. Но ни аксиомы, ни определения, ни ранее доказанные теоремы не могут быть ложными, следовательно, ложным должно быть допущение, то есть отрицание доказываемого предложения. Если же отрицание доказываемого предложения ложно, то само это предложение истинно, то есть теорема доказана. В качестве примера применения разделительного метода можно рассмотреть доказательство теоремы: «Если сумма противоположных углов четырехугольника равна К методам доказательства, выделенным по второму основанию, когда способ связи аргументов согласуется с определенной математической теорией в школьном курсе математики, относят: 1. Метод геометрических преобразований.Используется как средство обоснования некоторых отношений между элементами евклидовой геометрии. Он состоит из выполнения последовательности шагов: выбирается геометрическое преобразование, обладающее свойством, которое позволяет обосновать наличие указанного отношения между объектами евклидовой геометрии; выполняется преобразование, при котором один объект переходит в другой; обосновывается наличие указанного отношения между объектами с помощью свойств выбранного геометрического преобразования. 2. Алгебраические методы(уравнений, неравенств, тождественных преобразований). 3. Векторный метод,использующий аппарат векторной алгебры. 4. Координатный метод— способ определения положения точки на прямой, на плоскости или в пространстве с помощью чисел (например, в декартовой системе координат или какой-либо другой). Используя координатный метод, алгебраические уравнения можно истолковать в виде геометрических образов (графиков или фигур) и, наоборот, искать решение геометрических задач с помощью аналитических выражений (уравнений, неравенств или их систем). При доказательстве математических утверждений используются разные математические методы. Для того чтобы учащиеся овладели прямым и косвенным доказательствами, необходимо сформировать у них определенную последовательность умений: искать доказательство, проводить доказательство, оформлять доказательство теоремы. Выбор и использование того или иного метода доказательства теоремы во многом определяется его сущностью и взаимными связями, используемыми методами обучения, содержанием и местом теоремы в общей системе обучения математике в школе, возможностями активизации познавательной деятельности учащихся.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ), принадлежащую данной теории, которая удовлетворяет двум условиям:
), принадлежащую данной теории, которая удовлетворяет двум условиям: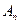 ) есть предложение Т.
) есть предложение Т. 2 и а
2 и а  132
132  .
. .
. .
.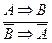 .
. ( Р(х) => Q(х)). Допускается, что Q(х) ложно. Тогда должно быть истинно
( Р(х) => Q(х)). Допускается, что Q(х) ложно. Тогда должно быть истинно  . На основе
. На основе  . Поэтому R(х) ложно, и принятое за истинное
. Поэтому R(х) ложно, и принятое за истинное  , то около четырехугольника можно описать окружность». Рассуждения строятся следующим образом: три точки, не лежащие на одной прямой, задают окружность, значит, любые три вершины четырехугольника принадлежат окружности; рассматриваются и отвергаются варианты, когда четвертая вершина лежит внутри или вне круга, ограниченного этой окружностью; делается вывод, что четвертая вершина лежит на данной окружности.
, то около четырехугольника можно описать окружность». Рассуждения строятся следующим образом: три точки, не лежащие на одной прямой, задают окружность, значит, любые три вершины четырехугольника принадлежат окружности; рассматриваются и отвергаются варианты, когда четвертая вершина лежит внутри или вне круга, ограниченного этой окружностью; делается вывод, что четвертая вершина лежит на данной окружности.