
|
|
Решение вспомогательной задачи оптимального управленияЧистяков С.В., Ишханова М.В. Математические модели выбора налоговых шкал. СПб., 1998. Естественно, что нумерация формул другая. Я только исправил те номера, где ссылка на формулы из моей книги. Кроме того, в приводимом фрагменте пособия функция выигрыша обозначена не через T, а через S. Р.О. Смирнов. Сергей Владимирович Чистяков, Марина Владимировна Ишханова МАТЕМАТИЧЕСКИЕ МОДЕЛИ ВЫБОРА НАЛОГОВЫХ ШКАЛ Учебное пособие Зав. редакцией Г.Чередниченко Редактор Ф. Бастиан Техн. редактор Л.Иванова Лицензия ЛР № 040050 от 15.08.96. Подписано в печать с оригинала-макета 17.06.98. Ф-т 60 ´ 84 / 16. Печать офсетная. Усл.печ.л. 3,02. Уч.-изд. л. 2,85. Тираж 200 экз. Заказ №
Редакция оперативной подготовки учебно-методических и научных изданий Издательства Санкт-Петербургского университета. 199034, С.-Петербург, Университетская наб., 7/ 9.
Центр оперативной полиграфии Санкт-петербургского университета. 199034, С.-Петербург, наб. Макарова, 6 . Литература 1. Инструкция № 35 по применению закона Российской Федерации о подоходном налоге с физических лиц с изменениями и дополнениями. М.: Изд-во “Ось-89”, 1995. 96 с.
2. Your Federal Income Tax. Publication 17. IRS, 1990.
3. Львов Ю.А. Основы экономики и организации бизнеса. СПб.: ГМП “Формика”, 1992. 383 с.
4. Смирнов Р.О., Чистяков С.В. О ставках налогообложения как инструменте государственного регулирования // Экономика и мат. методы. 1993. Т.29. Вып.2. С. 268–274.
5. Филиппов А.Ф. Дифференциальные уравнения с разрывной правой частью. М.: Наука, 1985. 224 с.
6. Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.:Наука, 1969. 392 с.
7. Рудин У. Основы математического анализа. М.: Мир, 1976. 319 c.
8. Зангвил У.И. Нелинейное программирование: Единый подход: Пер.с англ. М.: Сов. радио, 1973. 312 с.
9. Пшеничный Б.Н., Данилин Ю.М. Численные методы в экстремальных задачах. М.: Наука, 1975. 96 с. Оглавление Предисловие............................................................................................................ 3 § 1. Класс допустимых налоговых шкал................................................... 4 § 2. Функция распределения доходов и задача об определении суммы налога 8 § 3. Теоретико-игровая модель выбора шкалы средних ставок налога. 13 § 4. Вспомогательная задача оптимального управления: условие допустимости. 16 § 5. Решение вспомогательной задачи оптимального управления.. 21 § 6. Исследование теоретико-игровой модели....................................... 27 § 7. Основные ограничения на выбор шкалы маргинальных ставок налога 31 § 8. Восстановление таблицы налогов по оптимальной модельной шкале. 39 § 9. Упражнения и задачи для самостоятельных исследований...... 44 Литература........................................................................................................... 50 С целью доказательства того, что в игре Г существует доминирующая стратегия 1-го игрока, запишем формулу (2.1.14) с учетом условий (2.1.17) в следующем виде:
где Теперь рассмотрим “усеченную” антагонистическую игру
Из определения игр
будет доминирующей стратегией 1-го игрока в игре Для доказательства существования доминирующей стратегии 1-го игрока в игре
где Очевидно, что если будет доказано, что задача имеет решение, не зависящее от выбранной функции
Поэтому задача на максимум функционала (2.1.23) при ограничениях (2.1.15) – (2.1.17) равносильна следующей задаче оптимального управления:
Выясним условия существования допустимого управления в этой задаче, а, следовательно, непустоты множества стратегий 1-го игрока в игре
В результате этой замены задача (4.6) – (4.10) примет вид
Очевидно, что если будет установлено условие существования допустимого управления в задаче (4.16) – (4.20), то, пользуясь зависимостями (4.11) – (4.15) между функциями и параметрами этой задачи и функциями и параметрами задачи (4.6) – (4.10), будет установлено и условие существования допустимого управления в задаче (4.6) – (4.10). Проинтегрируем уравнение (4.17) с начальным условием (4.19) для произвольного допустимого управления
Рассмотрим два постоянных управления
и, соответственно,
Эти управления могут и не быть допустимыми. По формуле (4.21) найдем соответствующие им решения уравнения (4.17) с начальным условием (4.19)
Поскольку предполагается, что
Отсюда с учетом формул (4.22) и (4.23) при
Поэтому если здесь управление
Очевидно, верно и обратное, т.е. если справедливо это неравенство, то в задаче (4.16) – (4.20) существует допустимое управление. Действительно, с учетом формул (4.22) и (4.23) неравенство (4.25) может быть переписано в виде
а это с учетом определения решений Таким образом, справедливо следующее утверждение.
Лемма 1. Для того чтобы в задаче (4.16) – (4.20) существовало допустимое управление, необходимо и достаточно, чтобы выполнялись неравенства (4.25).
Замечание 1. Если одно из нестрогих неравенств (4.25) выполняется как равенство, то, как следует из вывода этих неравенств, в задаче (4.16) – (4.20) существует единственное, с точностью до эквивалентности измеримых по Лебегу функций, допустимое управление. А именно этим единственным допустимым управлением будет постоянное управление
Замечание 2.Справедливо и обратное утверждение к утверждению, сформулированному в замечании 1. А именно если одно из постоянных управлений
Замечание 3.Если одно из нестрогих неравенств (4.25) выполняется как равенство, то с учетом замечания 1 одно из указанных в нем управлений и будет оптимальным (в силу единственности допустимого управления). В этом случае оптимальное управление, очевидно, не зависит от выбранной ранее функции В силу имеющихся связей (4.11) – (4.15) между задачами (4.6) – (4.10) и (4.16) – (4.20) из леммы 1 в качестве следствия получим следующее утверждение.
Лемма 2.Для того чтобы в задаче (4.6) – (4.10) существовало допустимое управление, необходимо и достаточно, чтобы выполнялось следующее неравенство:
Значение этого условия в конечном итоге состоит в том, что оно позволяет проверить, корректно ли поставлена исходная задача о построении оптимальной налоговой шкалы. В частности, если для выбранных каким-то образом параметров Решение вспомогательной задачи оптимального управления Найдем теперь решение задачи (4.16) – (4.20). Тогда с учетом связи (4.11) – (4.15) между задачами (4.6) – (4.10) и (4.16) – (4.20) мы сможем найти и решение задачи (4.6) – (4.10). При этом нас будет интересовать не собственно само оптимальное управление в этой задаче, а соответствующее ему решение краевой задачи (4.7) – (4.10). Для решения задачи (4.16) – (4.20) воспользуемся принципом максимума Л. С. Понтрягина. При этом отметим, что с учетом замечаний 1 и 3 достаточно рассмотреть только тот случай, когда оба неравенства (4.25) являются строгими. Функция Гамильтона в задаче (4.16) – (4.20) имеет вид
поэтому сопряженное уравнение, в свою очередь, выглядит следующим образом:
В соответствии с принципом максимума можно утверждать, что для оптимального управления
и такое нетривиальное решение
которое в рассматриваемой задаче принимает вид
Отсюда видно, что если величина
знакоопределенная, то точка максимума функции, стоящей справа в равенстве (5.4), единственная и в силу того, что
Любое решение (4.21) однородного дифференциального уравнения (4.17) с начальными условиями (4.19) является положительным, поэтому положительным будет и любое решение краевой задачи (4.17) – (4.20). Следовательно,
Кроме того, в формуле (5.6)
так как Поэтому из формул (5.6) и условий (5.7) и (5.8) следует, что
Для дальнейшего уточнения вида оптимального управления
где
Заметим, что функция
либо имело бы вид
а это в соответствии с замечанием 2 означало бы, что одно из нестрогих неравенств (4.25) должно выполняться как равенство. Это, однако, противоречит сделанному предположению, что оба эти неравенства строгие. Обозначим
(в противном случае функция Поскольку ранее было сделано предположение о том, что
Для окончательного определения вида оптимального управления найдем точку его переключения 1) найти соответствующее управлению 2) найти соответствующее управлению 3) решить относительно
Решение этого уравнения и будет искомой точкой Интегрируя уравнение (4.17) при указанных управлениях и начальных условиях, получим
Подставляя эти формулы в формулу (5.13) и разрешая относительно
Таким образом, доказано следующее утверждение.
Лемма 3.Если оба неравенства (4.25) выполняются как строгие, то в задаче (4.16) – (4.20) существует единственное, с точностью до эквивалентности измеримых по Лебегу функций, оптимальное управление, которое имеет вид (5.12), при этом точка переключения оптимального управления находится по формуле (5.16). Из определения решений
а в явном виде в силу установленных формул (5.14) и (5.15)
Учитывая связь между задачей (4.16) – (4.20) и задачей на максимум функционала (4.6) при ограничениях (4.7) – (4.10), решение
Подставляя выражение (5.17) в формулу (5.18) и учитывая, что согласно формулам (4.13) – (4.15)
где в соответствии с формулой (5.16)
Таким образом, нами доказана следующая лемма.
Лемма 4.Если оба неравенства (4.27) выполняются как строгие, то решение задачи на максимум функционала (4.1) при ограничениях (4.2) – (4.4) имеет вид (5.19), где точка Заметим, что указанное в лемме 4 решение не зависит от выбранной функции 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , (2.1.21)
, (2.1.21) .
. , в которой множество стратегий 1-го (2-го) игрока совпадает с множеством
, в которой множество стратегий 1-го (2-го) игрока совпадает с множеством  всех функций, каждая их которых представляет собой сужение на промежуток
всех функций, каждая их которых представляет собой сужение на промежуток  той или иной функции
той или иной функции  , а функция выигрыша
, а функция выигрыша  имеет вид
имеет вид ,
,  .
. и
и  следует, что если будет доказано существование доминирующей стратегии 1-го игрока
следует, что если будет доказано существование доминирующей стратегии 1-го игрока  в игре
в игре  такая, что
такая, что (2.1.22)
(2.1.22) естественно считать оптимальной модельной шкалой средних ставок налога при заданных параметрах
естественно считать оптимальной модельной шкалой средних ставок налога при заданных параметрах  ,
,  ,
,  ,
,  ,
,  .
. зафиксируем произвольную стратегию 2-го игрока
зафиксируем произвольную стратегию 2-го игрока  и рассмотрим задачу на максимум функционала
и рассмотрим задачу на максимум функционала , (2.1.23)
, (2.1.23) .
. дифференцируема и имеет при почти всех
дифференцируема и имеет при почти всех  положительную производную
положительную производную  . В этом случае интеграл Стилтьеса сводится к обычному интегралу Римана:
. В этом случае интеграл Стилтьеса сводится к обычному интегралу Римана: .
. , (4.6)
, (4.6) , (4.7)
, (4.7) (4.8)
(4.8) ,
, , (4.9)
, (4.9) (4.10)
(4.10) .
. , (4.11)
, (4.11) , (4.12)
, (4.12) , (4.13)
, (4.13) , (4.14)
, (4.14) . (4.15)
. (4.15) , (4.16)
, (4.16) , (4.17)
, (4.17) , (4.18)
, (4.18)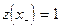 , (4.19)
, (4.19) (4.20)
(4.20) .
. . В итоге получим
. В итоге получим . (4.21)
. (4.21) ,
, 
 ,
,  .
. , (4.22)
, (4.22) . (4.23)
. (4.23) при почти всех
при почти всех  , то для решений (4.21), (4.22) и (4.23) будет справедливо неравенство
, то для решений (4.21), (4.22) и (4.23) будет справедливо неравенство .
. , получим
, получим . (4.24)
. (4.24) является допустимым в задаче (4.16) – (4.20), т.е. если
является допустимым в задаче (4.16) – (4.20), т.е. если  , то должно выполняться неравенство
, то должно выполняться неравенство . (4.25)
. (4.25) , (4.26)
, (4.26) и
и  , а также с учетом теоремы о непрерывной зависимости решений дифференциального уравнения от параметров означает, что в задаче (4.16) – (4.20) существует, и при этом постоянное, допустимое управление
, а также с учетом теоремы о непрерывной зависимости решений дифференциального уравнения от параметров означает, что в задаче (4.16) – (4.20) существует, и при этом постоянное, допустимое управление  ,
,  .
. является допустимым в задаче (4.16) – (4.20), то в первом случае левое из неравенств будет выполняться как равенство, а во втором, соответственно, правое из этих неравенств будет выполняться как равенство. Причем в обоих этих случаях других допустимых управлений, с точностью до эквивалентности измеримых по Лебегу функций, в задаче (4.16) – (4.20) нет.
является допустимым в задаче (4.16) – (4.20), то в первом случае левое из неравенств будет выполняться как равенство, а во втором, соответственно, правое из этих неравенств будет выполняться как равенство. Причем в обоих этих случаях других допустимых управлений, с точностью до эквивалентности измеримых по Лебегу функций, в задаче (4.16) – (4.20) нет. .
. . (4.27)
. (4.27) ,
,  ,
,  ,
,  ,
,  неравенство (4.27) не выполняется, то необходимо скорректировать выбор всех или некоторых из этих параметров.
неравенство (4.27) не выполняется, то необходимо скорректировать выбор всех или некоторых из этих параметров. , (5.1)
, (5.1) . (5.2)
. (5.2) в задаче (4.16) – (4.20) найдется такая постоянная
в задаче (4.16) – (4.20) найдется такая постоянная (5.3)
(5.3)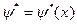 сопряженного уравнения (5.2), что для них и для решения
сопряженного уравнения (5.2), что для них и для решения  уравнения (4.17), соответствующего оптимальному управлению
уравнения (4.17), соответствующего оптимальному управлению  , при почти всех
, при почти всех  ,
, (5.4)
(5.4) (5.5)
(5.5) , эта точка совпадает либо с точкой
, эта точка совпадает либо с точкой  , если величина (5.5) отрицательная, либо, соответственно, с точкой
, если величина (5.5) отрицательная, либо, соответственно, с точкой  , если величина (5.5) положительная. Поэтому
, если величина (5.5) положительная. Поэтому (5.6)
(5.6) ,
,  . (5.7)
. (5.7) , (5.8)
, (5.8) .
. (5.9)
(5.9) сопряженного уравнения (5.2) по формуле Коши для линейного неоднородного дифференциального уравнения 1-го порядка
сопряженного уравнения (5.2) по формуле Коши для линейного неоднородного дифференциального уравнения 1-го порядка , (5.10)
, (5.10) .
. . Действительно, если бы решение
. Действительно, если бы решение  ,
, ,
, выражение, стоящее в квадратных скобках в правой части равенства (5.10). Так как функция
выражение, стоящее в квадратных скобках в правой части равенства (5.10). Так как функция  , то теми же свойствами обладает и функция
, то теми же свойствами обладает и функция  . Поэтому неравенство (5.3) должно быть строгим:
. Поэтому неравенство (5.3) должно быть строгим: (5.11)
(5.11) была бы тождественно равна постоянной
была бы тождественно равна постоянной  ).
). при почти всех
при почти всех  , то на основании неравенства (5.11) можно утверждать, что функция
, то на основании неравенства (5.11) можно утверждать, что функция  , а следовательно, и уравнение
, а следовательно, и уравнение  имеет на этом интервале единственное решение
имеет на этом интервале единственное решение  . В силу того что в точках
. В силу того что в точках  функции
функции  имеют одинаковые знаки,
имеют одинаковые знаки,  при
при  и
и 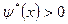 при
при  . Поэтому теперь можно уточнить, что формула (5.9) имеет вид
. Поэтому теперь можно уточнить, что формула (5.9) имеет вид (5.12)
(5.12) . Поскольку для оптимального управления
. Поскольку для оптимального управления  решение уравнения (4.17)
решение уравнения (4.17)  , которое удовлетворяет начальному условию (4.19);
, которое удовлетворяет начальному условию (4.19); решение уравнения (4.17)
решение уравнения (4.17)  , которое удовлетворяет начальному условию (4.20);
, которое удовлетворяет начальному условию (4.20); уравнение
уравнение . (5.13)
. (5.13) , (5.14)
, (5.14) . (5.15)
. (5.15) (5.16)
(5.16) уравнения (4.17) с учетом вида оптимального управления
уравнения (4.17) с учетом вида оптимального управления  краевой задачи (4.17) – (4.20) имеет вид
краевой задачи (4.17) – (4.20) имеет вид
 (5.17)
(5.17) последней задачи найдем теперь по формуле
последней задачи найдем теперь по формуле . (5.18)
. (5.18) ,
,  (5.19)
(5.19) (5.20)
(5.20) , причем эта лемма доказана здесь при дополнительном предположении о том, что функция
, причем эта лемма доказана здесь при дополнительном предположении о том, что функция  дифференцируема и имеет при почти всех
дифференцируема и имеет при почти всех  положительную производную.
положительную производную.