
|
|
И вращательного движения твердого телаПри поступательном движении все точки тела двигаются одинаково, поэтому для описания поступательного движения твердого тела достаточно описать движение хотя бы одной его точки. Если в качестве этой точки выбрать центр масс тела (т. С), то для этого можно использовать теорему о движении центра масс (38) или в проекции на оси координат:
Для описания вращательного движения воспользуемся теоремой об изменении момента количества движения системы (44) в проекции на ось z (ось вращения):
Дифференциальные уравнения плоского движения Плоское движение твердого тела можно представить как сумму двух движений: поступательного – вместе с центром масс и вращательного – вокруг центра масс. Отсюда следует, что для описания плоского движения необходимо описать движение его центра масс, а для этого можно использовать теорему о движении центра масс (38) в проекции на плоскость движения (Oxy):
Для описания вращательной составляющей плоского движения можно использовать теорему об изменении момента количества движения системы в относительном движении по отношению к центру масс, которая имеет вид, аналогичный (44):
Учитывая, что (45):
Принцип Даламбера для точки и системы Полученные ранее теоремы выведены из основного уравнения динамики. Те же теоремы можно получить и исходя из других положений, которые называются принципами механики. Принцип Даламбера для точки формулируется так: если к активным силам и силам реакций связей, действующим на точку добавить силу инерции, то такая система сил будет уравновешенной:
Здесь обозначено:
что эквивалентно (1). Применяя принцип Даламбера для каждой точки системы, получим
Здесь Если к каждой точке системы кроме внешних и внутренних сил, действующим на нее, приложить силу инерции, то такая система сил будет уравновешенной. Принцип Даламбера часто называют методом кинетостатики, поскольку он позволяет решать задачи динамики путем составления уравнений равновесия, т.е. методами статики.
Главный вектор и главный момент сил инерции Определение: главным вектором сил инерции называется вектор, равный геометрической сумме векторов сил инерции. Просуммировав уравнения (51) с учетом того, что по свойствам внутренних сил (32)
Определение: главным моментом сил инерции относительно точки О (оси), называется пара сил с моментом, равным геометрической сумме моментов сил инерции относительно той же точки (оси).
Поскольку система сил, определяемых уравнением (51) является уравновешенной, то для нее справедливо равенство:
Просуммировав уравнения (52) с учетом того, что по свойствам внутренних сил (32)

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ;
;  ;
;  .
. . Кинетический момент твердого тела относительно оси вращения найдем по формуле (45). В результате получим:
. Кинетический момент твердого тела относительно оси вращения найдем по формуле (45). В результате получим:  . Поскольку момент инерции тела – величина постоянная: Jz = const, то, вынеся его за знак производной, получим
. Поскольку момент инерции тела – величина постоянная: Jz = const, то, вынеся его за знак производной, получим  или
или  – это и есть дифференциальное уравнение вращательного движения твердого тела. Поскольку
– это и есть дифференциальное уравнение вращательного движения твердого тела. Поскольку  - угловое ускорение, то это уравнение можно записать в виде:
- угловое ускорение, то это уравнение можно записать в виде:  или
или  . Можно заметить, что это уравнение по своей структуре аналогично основному уравнению динамики (1). При его решении могут возникнуть две задачи динамики: прямая и обратная.
. Можно заметить, что это уравнение по своей структуре аналогично основному уравнению динамики (1). При его решении могут возникнуть две задачи динамики: прямая и обратная. ;
;  , или в проекции на ось перпендикулярную плоскости движения:
, или в проекции на ось перпендикулярную плоскости движения: . (48)
. (48)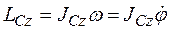 , находим
, находим  . Таким образом, получили три уравнения, которые и называются дифференциальными уравнениями плоского движения:
. Таким образом, получили три уравнения, которые и называются дифференциальными уравнениями плоского движения: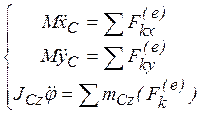 (49)
(49) . (50)
. (50) – равнодействующая активных (заданных) сил, действующих на точку;
– равнодействующая активных (заданных) сил, действующих на точку;  – равнодействующая сил реакций;
– равнодействующая сил реакций; 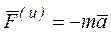 - сила инерции. Нетрудно увидеть, что принцип Даламбера для точки эквивалентен основному уравнению динамики (1). Действительно, подставив в (50) выражение для силы инерции, получим
- сила инерции. Нетрудно увидеть, что принцип Даламбера для точки эквивалентен основному уравнению динамики (1). Действительно, подставив в (50) выражение для силы инерции, получим ,
,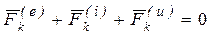 , k = 1…n. (51)
, k = 1…n. (51) ,
,  – соответственно равнодействующие внешних и внутренних сил, действующих на точку с номером k,
– соответственно равнодействующие внешних и внутренних сил, действующих на точку с номером k,  - сила инерции точки с номером k. Принцип Даламбера для системы (51) представляет собой n уравнений и формулируется так:
- сила инерции точки с номером k. Принцип Даламбера для системы (51) представляет собой n уравнений и формулируется так: .
. а по теореме о движении центра масс (38):
а по теореме о движении центра масс (38):  , получим
, получим
 ,
,  .
. , k = 1…n. (52)
, k = 1…n. (52) а по теореме об изменении момента количества движения системы (44):
а по теореме об изменении момента количества движения системы (44):  , получим
, получим  ,
, 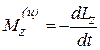 .
.