Доказать чему равна работа внутренних сил, приложенных к твердому телу.
 М1 и М2 - точки ТТ. Их силы взаимод., по III з-ну Ньютона, равны между собой и направлены по прямой М1М2 в противопол. стороны: М1 и М2 - точки ТТ. Их силы взаимод., по III з-ну Ньютона, равны между собой и направлены по прямой М1М2 в противопол. стороны:  . .
Сум. элем. работ этих сил:  . .  - единичный вектор, направл по направлению 1-ой силы. Тогда: - единичный вектор, направл по направлению 1-ой силы. Тогда:  .Используя эти соотношения, запишем: .Используя эти соотношения, запишем:
  . Проекции скоростей двух точек ТТ на направл. прямой, соед. эти точки, равны. Следовательно, скобка: . Проекции скоростей двух точек ТТ на направл. прямой, соед. эти точки, равны. Следовательно, скобка:  . Поэтому сумма элемент., а следовательно, полных работ внутренних сил твердого тела равна нулю. . Поэтому сумма элемент., а следовательно, полных работ внутренних сил твердого тела равна нулю.
Дать определение кинетической энергии точки и механической системы. Сформулировать и доказать теорему Кенига.
- Мера движения материальной точки, равная половине произведения массы точки на квадрат её скорости, называется её кинетической энергией.
- Мера движения системы материальных точек, равная сумме кинетических энергия всех точек входящих в систему, называется ее кинетической энергией.
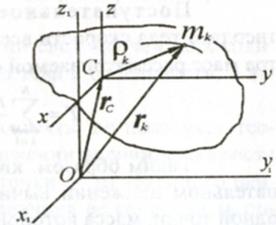 Абсолютное движение системы: переносное вместе с центром масс и относительное по отношению к центру масс. Абсолютное движение системы: переносное вместе с центром масс и относительное по отношению к центру масс.
Положение k-ой точки по отн. к О:  (1). Дифференцирую (1) по t: (1). Дифференцирую (1) по t:  , где: , где:  - абсолютная скорость k-ой точки системы, - абсолютная скорость k-ой точки системы, 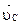 - абсолютная скорость ц. м., - абсолютная скорость ц. м., 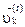 - относит. скорость k-ой точки относительно Сxyz. Поставим абсолютную скорость точки в уравнение: - относит. скорость k-ой точки относительно Сxyz. Поставим абсолютную скорость точки в уравнение:  . .
Получим:  . Стат. момент массы мех. системы относит. ц. м. равен нулю: . Стат. момент массы мех. системы относит. ц. м. равен нулю: 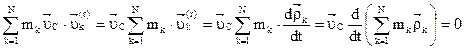 . .
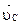 не зависит от индекса суммир., не зависит от индекса суммир., 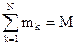 - масса системы, в итоге: - масса системы, в итоге:  . .
Кинетическая энергия механической системы в её абсолютном движении равна сумме кинетической энергии центра масс, если в нём сосредоточить массу всей системы, и кинетической энергии системы в её движении относительно центра масс.
Доказать формулы для вычисления кинетической энергии твердого тела в различных случаях его движения.
Поступат.: скорости всех его точек одинаковы и равны скорости центра масс ТТ:  . .
Вращат.: скорость произвольной точки ТТ равна: 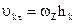 , где , где  - расстояние от точки до оси Оz. - расстояние от точки до оси Оz.  , где , где  - момент инерции тела относит. оси вращения Оz. - момент инерции тела относит. оси вращения Оz.
Плоск.: рассм. такое движение, как совокуп. поступат. движения тела вместе с центром масс С и вращат. вокруг подвижной оси Сz, движущейся поступат. вместе с центром масс. Относит. скорость точки тела равна:  . Подставив эту скорость в формулу Кенига: . Подставив эту скорость в формулу Кенига:  , получим: , получим:  . .
Сформулировать и доказать теорему о кинетической энергии материальной точки в различных формах.
Материальная точка массой m, движется под действием равнодействующей сил, которая равна  . ДУ движения точки в векторной форме: . ДУ движения точки в векторной форме:  или или  . Т.к. масса постоянна: . Т.к. масса постоянна:  (1). Умножим (1) скалярно на (1). Умножим (1) скалярно на  : :  (2). В левой части (2) внесем (2). В левой части (2) внесем  под знак производной: под знак производной:  (3): производная по времени от кинетической энергии точки равна мощности всех действующих на точку сил. (3): производная по времени от кинетической энергии точки равна мощности всех действующих на точку сил.
Умножая (3) на dt и заменяя  : :  (4): дифференциал от кинетической энергии точки равен элементарной работе всех действующих на точку сил. (4): дифференциал от кинетической энергии точки равен элементарной работе всех действующих на точку сил.
Интегрируя обе части (4) от положения М0 до М, имеем:  : изменение кинетической энергии точки при ее перемещении из одного положения в другое равно полной работе всех действующий на точку сил на этом же перемещении. : изменение кинетической энергии точки при ее перемещении из одного положения в другое равно полной работе всех действующий на точку сил на этом же перемещении.
Сформулировать и доказать теорему о кинетической энергии механической системы различных формах.
Система N материальных точек. Масса k-ой точки - 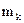 . К каждой k-ой точке системы (k = 1, 2, ..., N) прилож. равнодействующие внешних . К каждой k-ой точке системы (k = 1, 2, ..., N) прилож. равнодействующие внешних  и внутренних и внутренних  сил. сил.
ДУ движения:  или или  (1). Т.к. масса постоянна внесём ее под знак производной и умножим (1) скалярно на (1). Т.к. масса постоянна внесём ее под знак производной и умножим (1) скалярно на  : :  (2). Внося (2). Внося  под знак производной, суммируем (2) по k и поменяем знаки суммир. и дифференцир. местами: под знак производной, суммируем (2) по k и поменяем знаки суммир. и дифференцир. местами:  или или  (2): производная по времени от кинетической энергии системы равна сумме мощностей всех действующих на систему внешних и внутренних сил. (2): производная по времени от кинетической энергии системы равна сумме мощностей всех действующих на систему внешних и внутренних сил.
Умножим (2) слева и справа на dt и учтём, что  : :  или или  (3): дифференциал кинетической энергии механической системы равен сумме элементарных работ всех действующих на систему внешних и внутренних сил. (3): дифференциал кинетической энергии механической системы равен сумме элементарных работ всех действующих на систему внешних и внутренних сил.
Проинтегрируем обе части (3) от нач. положения системы до конеч., изменяя порядок суммир. и интегрир.:  или или  : изменение кинетической энергии механической системы при ее перемещении из одного положения в другое равно сумме полных работ всех действующих на систему внешних и внутренних сил на соответствующем перемещении. : изменение кинетической энергии механической системы при ее перемещении из одного положения в другое равно сумме полных работ всех действующих на систему внешних и внутренних сил на соответствующем перемещении.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


 М1 и М2 - точки ТТ. Их силы взаимод., по III з-ну Ньютона, равны между собой и направлены по прямой М1М2 в противопол. стороны:
М1 и М2 - точки ТТ. Их силы взаимод., по III з-ну Ньютона, равны между собой и направлены по прямой М1М2 в противопол. стороны:  .
. .
.  - единичный вектор, направл по направлению 1-ой силы. Тогда:
- единичный вектор, направл по направлению 1-ой силы. Тогда:  .Используя эти соотношения, запишем:
.Используя эти соотношения, запишем:
 . Проекции скоростей двух точек ТТ на направл. прямой, соед. эти точки, равны. Следовательно, скобка:
. Проекции скоростей двух точек ТТ на направл. прямой, соед. эти точки, равны. Следовательно, скобка:  . Поэтому сумма элемент., а следовательно, полных работ внутренних сил твердого тела равна нулю.
. Поэтому сумма элемент., а следовательно, полных работ внутренних сил твердого тела равна нулю. Абсолютное движение системы: переносное вместе с центром масс и относительное по отношению к центру масс.
Абсолютное движение системы: переносное вместе с центром масс и относительное по отношению к центру масс. (1). Дифференцирую (1) по t:
(1). Дифференцирую (1) по t:  , где:
, где:  - абсолютная скорость k-ой точки системы,
- абсолютная скорость k-ой точки системы, 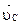 - абсолютная скорость ц. м.,
- абсолютная скорость ц. м., 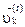 - относит. скорость k-ой точки относительно Сxyz. Поставим абсолютную скорость точки в уравнение:
- относит. скорость k-ой точки относительно Сxyz. Поставим абсолютную скорость точки в уравнение:  .
. . Стат. момент массы мех. системы относит. ц. м. равен нулю:
. Стат. момент массы мех. системы относит. ц. м. равен нулю: 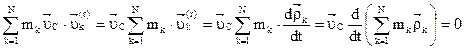 .
.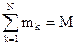 - масса системы, в итоге:
- масса системы, в итоге:  .
. .
.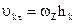 , где
, где  - расстояние от точки до оси Оz.
- расстояние от точки до оси Оz.  , где
, где  - момент инерции тела относит. оси вращения Оz.
- момент инерции тела относит. оси вращения Оz. . Подставив эту скорость в формулу Кенига:
. Подставив эту скорость в формулу Кенига:  , получим:
, получим:  .
. . ДУ движения точки в векторной форме:
. ДУ движения точки в векторной форме:  или
или  . Т.к. масса постоянна:
. Т.к. масса постоянна:  (1). Умножим (1) скалярно на
(1). Умножим (1) скалярно на  :
:  (2). В левой части (2) внесем
(2). В левой части (2) внесем  (3): производная по времени от кинетической энергии точки равна мощности всех действующих на точку сил.
(3): производная по времени от кинетической энергии точки равна мощности всех действующих на точку сил. :
:  (4): дифференциал от кинетической энергии точки равен элементарной работе всех действующих на точку сил.
(4): дифференциал от кинетической энергии точки равен элементарной работе всех действующих на точку сил. : изменение кинетической энергии точки при ее перемещении из одного положения в другое равно полной работе всех действующий на точку сил на этом же перемещении.
: изменение кинетической энергии точки при ее перемещении из одного положения в другое равно полной работе всех действующий на точку сил на этом же перемещении.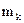 . К каждой k-ой точке системы (k = 1, 2, ..., N) прилож. равнодействующие внешних
. К каждой k-ой точке системы (k = 1, 2, ..., N) прилож. равнодействующие внешних  и внутренних
и внутренних  сил.
сил. или
или  (1). Т.к. масса постоянна внесём ее под знак производной и умножим (1) скалярно на
(1). Т.к. масса постоянна внесём ее под знак производной и умножим (1) скалярно на  :
:  (2). Внося
(2). Внося  или
или  (2): производная по времени от кинетической энергии системы равна сумме мощностей всех действующих на систему внешних и внутренних сил.
(2): производная по времени от кинетической энергии системы равна сумме мощностей всех действующих на систему внешних и внутренних сил. или
или  (3): дифференциал кинетической энергии механической системы равен сумме элементарных работ всех действующих на систему внешних и внутренних сил.
(3): дифференциал кинетической энергии механической системы равен сумме элементарных работ всех действующих на систему внешних и внутренних сил. или
или  : изменение кинетической энергии механической системы при ее перемещении из одного положения в другое равно сумме полных работ всех действующих на систему внешних и внутренних сил на соответствующем перемещении.
: изменение кинетической энергии механической системы при ее перемещении из одного положения в другое равно сумме полных работ всех действующих на систему внешних и внутренних сил на соответствующем перемещении.