
|
|
Теорема об изменении кинетической энергии.
Эта теорема существует в трех формах: в форме дифференциалов, в форме производной и в интегральной (конечной) форме. Первые две формы можно использовать для сил любой функциональной зависимости, а третью форму только для постоянных сил, или сил, зависящих только от перемещения точек приложения сил. Третью форму рационально использовать, если необходимо найти зависимость скорости от перемещения. Вторую форму, как правило, используют для определения ускорения.
Теорема об изменении кинетической энергии материальной точки:
1) В форме дифференциалов теорема утверждает, что: «Дифференциал кинетической энергии материальной точки равен элементарной работе равнодействующей сил, действующих на эту точку», то есть: 2) В форме производной теорема утверждает, что: «Производная по времени от кинетической энергии материальной точки равна мощности равнодействующей сил, действующих на эту точку», то есть: 3) В интегральной форме теорема утверждает, что: «Изменение кинетической энергии материальной точки, которое произошло на некотором ее перемещении, равно работе равнодействующей сил, действующих на эту точку», то есть: Т*,Т0 – значения кинетической энергии в конце и в начале перемещения.
Доказательство: На основании принципа независимости действия сил, можно записать, что:
Умножив скалярно левую и правую части последнего векторного равенства на дифференциал (
Если подвести скорость υ под символ дифференциала, то будем иметь выражение:
что соответствует утверждению первой формы теоремы. Если левую и правую части последнего векторного равенства разделить на дифференциал времени, то получим:
что соответствует утверждению второй формы теоремы. Если интегрировать выражение:
что соответствует утверждению третьей формы теоремы.
Пример 2.
Материальная точка массой m=2кг перемещается из положения М0 в положение М1, Причем ее скорость в этих точках υм0=8м/с и υм1=4м/с. Необходимо определить работу равнодействующей сил, действующих на материальную точку. Решение: Работа равнодействующей входит в интегральную форму теоремы об изменении кинетической энергии материальной точки:
В данном случае:
Теорема об изменении кинетической энергии механической системы:
Эта теорема в форме дифференциалов утверждает, что: «Дифференциал кинетической энергии T механической системы равен сумме элементарных работ всех внешних и всех внутренних сил, действующих на эту систему», то есть:
Доказательство: Для каждой материальной точки, входящей в механическую систему, закон о независимости действия сил имеет вид:
Умножая скалярно векторное равенство на дифференциал (
Сложив эти векторные равенства по индексу «k» и учитывая, что операции суммирования и нахождения дифференциалов можно поменять местами, получим:
что и требовалось доказать, так как Теорема об изменении кинетической энергии механической системы в форме производной утверждает, что: «Производная по времени от кинетической энергии механической системы равна сумме мощностей всех внешних и всех внутренних сил, действующих на эту систему», то есть:
Доказательство: Разделив на дифференциал времени (dt) левую и правую часть равенства (1), получим:
что и требовалось доказать. Теорема об изменении кинетической энергии в интегральной (конечной) форме утверждает, что: «Изменение кинетической энергии механической системы, которое произошло на некотором ее конечном перемещении, равно сумме работ на этом перемещении всех внешних и всех внутренних сил, действующих на эту систему», то есть:
Здесь T*, T0 – кинетическая энергия механической системы в конце и в начале перемещения. Доказательство: Интегрируя равенство (1), получим:
что и требовалось доказать. Можно показать, что, если на механическую систему наложены неизменяемые идеальные связи, то сумма работ внутренних сил, действующих на такую систему, будет равна нулю, то есть:
Механическая система представляет собой совокупность попарно взаимодействующих материальных точек, а действуют они друг на друга с силами равными по величине, направлены по одной прямой, но в противоположные стороны (см. рисунок).
Сумма элементарных работ таких сил:
Если механическая система неизменяемая, то
Тогда сумма работ всех внутренних сил, действующих на неизменяемую механическую систему:
Пример 1.
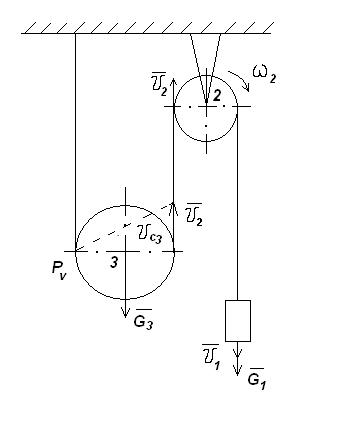
Определить скорость центра масс тела «3», когда груз «1» пройдет расстояние S1=2м, если массы тел m1=8кг, m2=4кг, m3=4кг, тела «2» и «3» представляют собой однородные диски с одинаковыми радиусами r=0,5м. В начальный момент времени данная механическая система находилась в покое. Решение: Эта механическая система состоит из тела «1», которое двигается поступательно, тела «2», которое совершает вращательное движение, и тела «3», которое движется плоско-параллельно. Поэтому:
Скорости υ1 , ω2 , ω3 должны быть выражены через скорость υс3, так как именно эту скорость необходимо определить.
Момент инерции: Тогда:
Данная механическая система является неизменяемой. Поэтому сумма работ всех внутренних сил равна нулю, то есть: Из внешних сил совершают работу только силы тяжести G1 и G2. Тогда: Работа от силы тяжести: Работа от силы тяжести: Перемещение точки C3 найдем, используя соотношение между скоростями υс3 и υ1, то есть: Тогда: Для определения зависимости между скоростью и перемещением применим теорему об изменении кинетической энергии в интегральной форме:
В начальный момент времени υс3=0 , поэтому Т0=0. Тогда:
Пример 2.
Два груза весом Р1 и Р2 подвешены на гибких нерастяжимых и невесомых нитях, которые намотаны на ступенчатый блок радиусами r и R и весом Р3. Момент инерции блока «3» относительно оси вращения J. Предполагая, что эта механическая система движется только под влиянием сил тяжести причем Р1*Р2>Р2*r и пренебрегая трением, необходимо определить угловое ускорение блока. Решение: Исследуемая механическая система неизменяемая, поэтому теорема об изменении ее кинетической энергии в диффренциальной форме имеет вид:
Грузы движутся поступательно, поэтому их кинетические энергии:
Блок «3» вращается вокруг неподвижной оси, поэтому:
Кинетические энергии отдельных тел и всей механической системы необходимо выразить через угловую скорость ω3, учитывая, что:
Сумма мощностей внешних сил, действующих на эту систему:
Мощности остальных сил равны нулю, так как точка приложения этих сил (т.О) неподвижная. Найдем мощности Р1 и Р2.
Тогда: Производная по времени от кинетической энергии данной механической системы
Подставляя найденные 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (1)
(1) (2)
(2) , где
, где или
или 
 , где R – равнодействующая.
, где R – равнодействующая. ) радиус-вектора, определяющего положение материальной точки и перегруппировав дифференциалы, получим:
) радиус-вектора, определяющего положение материальной точки и перегруппировав дифференциалы, получим: или
или  .
. или
или  ,
, или
или  или
или  ,
,

 , тогда
, тогда 
 (1)
(1) , k=1,2,…,n
, k=1,2,…,n  ) радиус-вектора и перегруппировав дифференциалы, получим:
) радиус-вектора и перегруппировав дифференциалы, получим: или
или  .
. или
или ,
,
 , k=1,2,3,…,n
, k=1,2,3,…,n или
или  , k=1,2,3,…,n (3)
, k=1,2,3,…,n (3) ,
, .
.

 , а следовательно
, а следовательно 



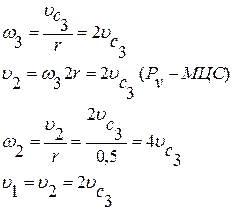

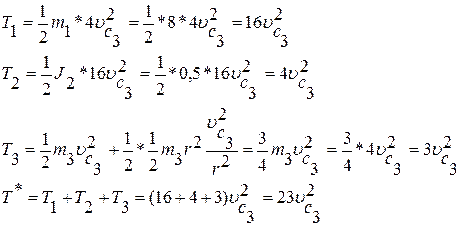




 . Поэтому:
. Поэтому:  .
.
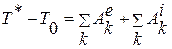
 , откуда при
, откуда при 
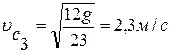

 (1)
(1)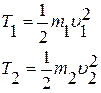

 , т.е.
, т.е. 
 .
.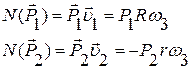
 .
.
 и
и  в равенство (1), получим
в равенство (1), получим  , откуда получим
, откуда получим 