
|
|
Теорема об изменении кинетического момента механической системыЭта теорема относительно центра утверждает, что: «Производная по времени от кинетического момента механической системы относительно центра (т.О) равна главному моменту всех внешних сил
здесь главный момент внешних сил Доказательство. Для каждой материальной точки, входящей в механическую систему основной закон динамики имеет вид
Умножив это векторное равенство на радиус
Но
Сложив эти векторные равенства по индексу «k» и учитывая, что операции сложения и нахождения произведений можно менять местами, получим
здесь:
Покажем, что главный момент внутренних сил
Вычислим сумму моментов от сил
Очевидно, что С учетом этого
Так как механическая система представляет собой совокупность попарно взаимодействующих материальных точек, то можно считать доказанным, что главный момент внутренних сил равен нулю, от есть Тогда равенство (8) с учетом изложенного выше принимает вид Теорема об изменении проекции кинетического момента относительно оси утверждает, что: «Производная по времени от проекции кинетического момента механической системы (от кинетического момента относительно любой оси) на любую ось рана проекции главного момента внешних сил, действующих на эту систему, на ту же ось». то есть
Проектируя векторное равенство (8) на ось, получим равенство (9). Следствия из теоремы об изменении момента количества движения материальной точки и кинетического момента механической системы. 1. Если момент равнодействующей сил, действующих на материальную точку, относительно какого-либо центра (т.О) равен нулю, то момент количества движения этой точки относительно того же центра есть величина постоянная, то есть если
2. если момент равнодействующей сил, действующих на материальную точку, относительно какой-либо оси равен нулю, то момент количества движения этой точки относительно той же оси есть величина постоянная, то есть
3. Если главный момент внешних сил, действующих на механическую систему относительно какого-либо центра равен нулю, то кинетический момент механической системы относительно этого же центра есть величина постоянная, то есть если
4. Если главный момент внешних сил, действующих на механическую систему, относительно какой-либо оси равен нулю, то кинетический момент этой системы относительно той же оси есть величина постоянная, то есть если Пример. Материальная точка массой m=0,5 кг движется по закону Решение Скорость материальной точки Момент количества движения материальной точки относительно начала отсчета
По теореме об изменении момента количества движения материальной точки
Пример.
По стержню АВ движется ползун с массой m=1 кг согласно закону АС=0,2+1,2t. Момент инерции вала ОА вместе со стержнем Jz=2,5 кг*м2. Определить угловую скорость ω1 при t1=1 с, если начальная угловая скорость ω0=10 с-1. Решение Объектом исследования является механическая система, состоящая из стержня, связанного жестко с валом и ползуна, который будем считать материальной точкой, причем ползун совершает сложное движение, состоящее из переносного вращательного движения вместе со стержнем и относительного прямолинейного движения. Силы, действующие на объект исследования показаны на рис.
Теорема об изменении кинетического момента этой механической системы относительно оси вращения «z» имеет вид Поэтому В начальный момент времени ползун находился на расстоянии АС0=0,2+1,2*0=0,2 м, а при t1=1 с АС=0,2+1,2+1=1,4 м. Для любого момента времени Здесь:
С учетом этого кинетический момент данной механической системы относительно оси Z для любого момента времени
Из формулы (1) 25,4=4,46 ω1
Пример Тело вращается вокруг вертикальной оси «Z» под действием пары сил с моментом Необходимо определить угловую скорость тела в момент времени t1=3 с, если в начальный момент тело не вращалось. Решение Для решения поставленной задачи применим теорему об изменении кинетического момента тела относительно оси вращения – оси Z:
В данном случае
или Разделяя переменные, получим Интегрируя, найдем Таким образом, закон изменения угловой скорости Если подставить сюда t1=3 с получим
Работа и мощность силы Элементарная работа силы dA на действительном перемещении точки ее приложения равна скалярному произведению силы
Если перейти к системе координат Эйлера, учитывая, что
здесь ds – дифференциал дуговой координаты, которая на уровне бесконечно малых величин совпадает с понятием пройденного пути точкой приложения силы. Если расписав скалярное произведение векторов в аналитическом виде, то формула (1) приобретает следующий вид
Здесь Формуле (2) можно придать несколько иной вид учитывая, что
здесь вращения, положение которого совпадает с мгновенным центром скоростей. Интегрируя выражения (1), (2), (3) и (4), найдем полную работу силы.
Интегралы (5), (6), (7) криволинейные, которые находятся с помощью специальных методов, однако, если удается получить функции только одной переменной эти интегралы превращаются в обыкновенные. Интеграл (8) всегда обычный, в чем его преимущество перед другими. Единица измерения работы силы очевидна из формулы (1)
Если левые и праве части выражений (1) и (4) разделить на дифференциал времени, то получим формулы по которым можно определить мощность силы.
Единицей измерения мощности силы является [ватт]=[н*м/с]. Формулы (8) и (10) можно использовать для вычисления, работы и мощности пар сил, соответственно. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , действующих на механическую систему с точкой приведения в центре, относительно которого определен кинетический момент, то есть
, действующих на механическую систему с точкой приведения в центре, относительно которого определен кинетический момент, то есть (7)
(7) .»
.»
 , определяющий положение k-ой материальной точки по отношению к центру (т.О), получим
, определяющий положение k-ой материальной точки по отношению к центру (т.О), получим .
. см. доказательство теоремы для материальной точки. Тогда
см. доказательство теоремы для материальной точки. Тогда
 (8)
(8) ;
; - главный момент внутренних сил.
- главный момент внутренних сил. . Для этого изобразим две материальные точки механической системы, взаимодействующий между собой с силами
. Для этого изобразим две материальные точки механической системы, взаимодействующий между собой с силами  (см. рисунок).
(см. рисунок).
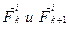 относительно произвольного центра (т.О).
относительно произвольного центра (т.О).
 , и тогда
, и тогда  .
. , так как
, так как 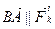 .
. , что и требовалось доказать.
, что и требовалось доказать. (9), здесь
(9), здесь 
 - проекция главного момента внешних сил на
- проекция главного момента внешних сил на , то
, то  так как только от постоянной величины производная всегда равна нулю.
так как только от постоянной величины производная всегда равна нулю.
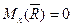 , то
, то  , откуда
, откуда  .
. , то
, то  , откуда
, откуда 
 , то
, то  , откуда
, откуда  .
. . Определить момент равнодействующей всех сил, приложенных к этой точки относительно начала координат.
. Определить момент равнодействующей всех сил, приложенных к этой точки относительно начала координат. .
.
 .
.
 - вес ползуна, G – вес стержня,
- вес ползуна, G – вес стержня,  - реакции связей. Очевидно, что моменты этих сил относительно оси вращения (z) равны нулю, так как эти силы или пересекают ось, или параллельны ей, тогда
- реакции связей. Очевидно, что моменты этих сил относительно оси вращения (z) равны нулю, так как эти силы или пересекают ось, или параллельны ей, тогда  .
. , откуда следует, что
, откуда следует, что  .
. (1)
(1) .
. - кинетический момент стержня относительно оси Z.
- кинетический момент стержня относительно оси Z. - момент количества движения ползуна относительно оси Z. Векторы количества переносного и относительного движений показаны на рисунке, причем
- момент количества движения ползуна относительно оси Z. Векторы количества переносного и относительного движений показаны на рисунке, причем  параллельны оси X. Моменты этих количеств движения относительно оси «Z»
параллельны оси X. Моменты этих количеств движения относительно оси «Z» 
 , так как вектор
, так как вектор  пересекает ось «Z».
пересекает ось «Z». , откуда
, откуда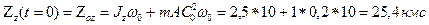


 . Момент инерции тела относительно оси вращения (OZ) Jz=3 кг м2
. Момент инерции тела относительно оси вращения (OZ) Jz=3 кг м2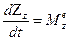 , где
, где 
 или
или  ,
, , или
, или  .
. .
. . Постоянную интегрирования e1 найдем по начальным условиям при t=0 ω0=0, откуда
. Постоянную интегрирования e1 найдем по начальным условиям при t=0 ω0=0, откуда  .
.

 на дифференциал
на дифференциал 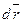 радиус-вектора , определяющего положение точки приложения этой силы, то есть
радиус-вектора , определяющего положение точки приложения этой силы, то есть (1)
(1)
 , то элементарную работу силы можно выразить следующим образом
, то элементарную работу силы можно выразить следующим образом , то есть
, то есть 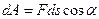 (2).
(2). (3)
(3) - проекции силы на соответствующие координатные оси; dx, dy, dz – дифференциалы координат, определяющих положение точки приложения силы.
- проекции силы на соответствующие координатные оси; dx, dy, dz – дифференциалы координат, определяющих положение точки приложения силы. , где
, где  - радиус кривизны траектории движения, а
- радиус кривизны траектории движения, а  - дифференциал угла смежности (См. естественный способ задания движения материальной точки).
- дифференциал угла смежности (См. естественный способ задания движения материальной точки). (4)
(4) -проекция силы на тангенциальную ось,
-проекция силы на тангенциальную ось, 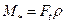 - момент силы F относительно центра кривизны траектории движения точки приложения силы . Следует учесть, что при вращательном движении тела центры кривизны всех его точек лежат на оси вращения, следовательно
- момент силы F относительно центра кривизны траектории движения точки приложения силы . Следует учесть, что при вращательном движении тела центры кривизны всех его точек лежат на оси вращения, следовательно  приобретает смысл момента силы относительно оси вращения, а при плоско-параллельном движении согласно теореме Шаля за центр кривизны следует принять мгновенный центр
приобретает смысл момента силы относительно оси вращения, а при плоско-параллельном движении согласно теореме Шаля за центр кривизны следует принять мгновенный центр , (5)
, (5) , (6)
, (6) , (7)
, (7) . (8)
. (8) , то есть [н*м]=[н]*[м], откуда следует, что единицей измерения работы силы джоуль – [н*м].
, то есть [н*м]=[н]*[м], откуда следует, что единицей измерения работы силы джоуль – [н*м]. , (9).
, (9). . (10)
. (10)