|
Алгоритм решения задач традиционным и координатно-векторным методом
| Что необходимо найти
| Алгоритм действий
| | Традиционный
| Координатно-векторный
| | Подготовка
|
| Ввести систему координат Oxyz
| | Построить чертёж, согласно условиям задачи. Для удобства подписать данные величины.
| | Расстояние между точками A и B
| Включить АВ в некоторый треугольник и найти его длину как сторону треугольника.
| 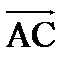 По формуле d = По формуле d = 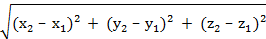
| | Расстояние от точки B до прямой AC
| Найти длину отрезка перпендикуляра, если удастся включить этот отрезок в некоторый треугольник (трапецию и т.д.) в качестве одной из высот.
| 1. Найти координаты вектора
 2. Найти координаты вектора
2. Найти координаты вектора
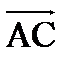  3. Найти косинус угла между и
4. Найти синус угла с помощью основного тригонометрического тождества.
5. Найти длину вектора: 3. Найти косинус угла между и
4. Найти синус угла с помощью основного тригонометрического тождества.
5. Найти длину вектора:
 | | = | | =  6. BD = AB sin
6. BD = AB sin 

| | Расстояние от точки M до плоскости
| Найти длину перпендикуляра, опущенного из этой точки на плоскость.
1. Для этого нужно построить сечение, которое перпендикулярно плоскости и проходит через заданную точку.
2. Искомое расстояние будет равно высоте полученного нового многогранника.
| 1. Найти уравнение плоскости
a (x-x0) + b(y-y0) + c (z-z0) = 0
2. Найти расстояние
| d =
| |ax0 + by0 + cz0 + d|
| 
|
| | Расстояние между скрещива-ющимися прямыми
| 1. Построить общий перпендикуляр двух скрещивающихся прямых и найти его длину.
2. Построить плоскость, содержащую одну из прямых и параллельную второй. Тогда искомое расстояние будет равно расстоянию от точки до прямой, построенной в плоскости.
3. Заключить данные прямые в параллельные плоскости, проходящие через данные скрещивающиеся прямые, найти расстояние между этими плоскостями.
4. Построить плоскость, перпендикулярную одной из этих прямых и построить проекцию второй прямой.
| 1. Провести через любую точку прямой a прямую c параллельную прямой b
2. Прямые a и c задают плоскость  , которая параллельна прямой b.
3. Найти расстояние от любой точки прямой b до плоскости , которая параллельна прямой b.
3. Найти расстояние от любой точки прямой b до плоскости  . Оно равно расстоянию между прямыми a и b. . Оно равно расстоянию между прямыми a и b.
| | Угол между двумя прямыми
| 1. Достроить до треугольника, в котором одна из сторон является той, расстояние от которой находится (с), а вторая сторона (b) параллельна скрещивающейся прямой.
2. По теореме косинусов
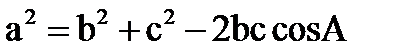
| 1. Найти координаты направляющих векторов.
2. По формуле

| | Угол между прямой и плоскостью
| 1. Включить угол в прямоугольный треугольник в качестве одного из острых углов.
2. Найти необходимые элементы треугольника.
3. Через соотношения величин в треугольнике найти угол.
| 1. Найти координаты направляющего вектора прямой.
2. Задать уравнение плоскости.
3. Из уравнения плоскости получить уравнение нормального вектора.
 4. Найти угол между нормальным вектором и направляющим вектором прямой. 4. Найти угол между нормальным вектором и направляющим вектором прямой.
| | Угол между плоскостями
| 1. Определить линейный угол между этими плоскостями.
2. Найти величину линейного угла (угол между прямыми).
| 1. Задать плоскости уравнениями.
2. Определить координаты нормальных векторов плоскости.
3. Найти угол между нормальными векторами.
| | Площади сечений, поверхностей, объёмов тел
| 1. Найти необходимые элементы, используя шаги, описанные выше.
2. С помощью формулы найти площадь (объем).
| | | | | |
Решение задач различными методами
Задача 1. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите косинус угла между прямыми AB1 и BC1.
Традиционный метод

Прямая BC1 принадлежит плоскости BCC1 , прямая AB1 пересекает эту плоскость в точке B1, не лежащей на прямой BC1 , следовательно, прямые AB1 и BC1 являются скрещивающимися. Через точку B1 проведем прямую, параллельную прямой BC1 , пусть K — точка пересечения этой прямой и плоскости ABC , тогда ⦟АВ1К — искомый по определению угла между скрещивающимися прямыми.
Найдем стороны ∆AB1K. KB1C1B — параллелограмм по построению, его противоположные стороны равны, то есть B1C1 = KB = 1. В основаниях правильной треугольной призмы лежат правильные треугольники, каждый из углов которых, равен по 60°. Значит ⦟KBA = 120°, как смежный с углом в 60° Сторону AK находим по теореме косинусов для треугольника ABK , получаем AK = 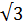 . Сторону KB находим по теореме Пифагора для прямоугольного треугольника KBB1, получаем KB1 = . Сторону KB находим по теореме Пифагора для прямоугольного треугольника KBB1, получаем KB1 = 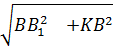 , то есть KB1 = , то есть KB1 =  . Сторону AB1 находим по теореме Пифагора для прямоугольного треугольника AA1B1, получаем AB1 = . Сторону AB1 находим по теореме Пифагора для прямоугольного треугольника AA1B1, получаем AB1 =  то есть AB1 = то есть AB1 =  . .
Зная три стороны треугольника, можно найти все его элементы. Искомый угол находим по теореме косинусов для треугольника AKB1, получаем AK2 = AB12 + KB12 – 2.AB1 . KB1 cos⦟AB1K, то есть -1 = -4cosAB1K, откуда cos⦟AB1K =0,25.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


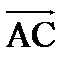 По формуле d =
По формуле d = 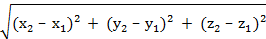
 2. Найти координаты вектора
2. Найти координаты вектора
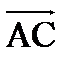
 3. Найти косинус угла между и
4. Найти синус угла с помощью основного тригонометрического тождества.
5. Найти длину вектора:
3. Найти косинус угла между и
4. Найти синус угла с помощью основного тригонометрического тождества.
5. Найти длину вектора:
 6. BD = AB sin
6. BD = AB sin 


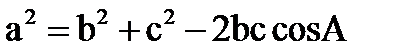


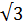 . Сторону KB находим по теореме Пифагора для прямоугольного треугольника KBB1, получаем KB1 =
. Сторону KB находим по теореме Пифагора для прямоугольного треугольника KBB1, получаем KB1 = 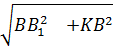 , то есть KB1 =
, то есть KB1 =  . Сторону AB1 находим по теореме Пифагора для прямоугольного треугольника AA1B1, получаем AB1 =
. Сторону AB1 находим по теореме Пифагора для прямоугольного треугольника AA1B1, получаем AB1 =  то есть AB1 =
то есть AB1 =