
|
|
Пример исследование производственной системы
Рассмотрим решение задачи построения траектории на основе полученных знаний о преобразовании Лапласа и передаточных функций. В качестве моделируемой системы возьмем некоторое производство, которое из поступающего сырья производит два вида продукции. При производстве продукции первого типа сырье подвергается двум переделам, а второго - одному. Из единицы сырья продукции первого типа получается 5 в некоторых единицах, а второго - 7. Сырье распределяется поровну для двух видов продукции. Длительность производственного процесса для первого типа продукции в первом переделе составляет 3, а во - втором - 6. Для второго типа продукции это составит 9. Сырье на вход всей системы подается с интенсивностью 4 в течение двух первых единиц времени. Требуется найти траекторию выхода продукции каждого типа. Указанных данных достаточно для того, чтобы представить структурную схему системы.
V2 0.5 3р+1
U
Рис. 13
Матричная передаточная функция состоит из двух компонент K1(p)=0.5*(5/(p+1))*(1/(2p+1)) и K2(p)=0.5*(7/(3p+1)). Входной сигнал представляется собой разность единичных функций, причем та которая вычитается, сдвинута на 2 ед. времени, т.е. u(t)=4*(1(t)-1(t-2)). Изображение входного сигнала имеет вид: u*(p)=4(1-e-2p). Таким образом, v*1(p)=K1(p)*u(p)=(1-e-2p)*10/((p+1)*(2p+1)) ( далее мы рассмотрим лишь более сложную задачу - нахождение v*1(t)). Для решения задачи нахождения обратного преобразования Лапласа существует несколько методов. Мы используем метод проверок. Он состоит в том, чтобы выразить обращаемую функцию так, чтобы она состояла из частей, в которых можно узнать известные преобразования Лапласа (публикуются специальные таблицы преобразований Лапласа). Для использования метода применяется следующая теорема.
Т е о р е м а. Пусть N(p)/D(p) правильная дробь31 и многочлены N(p) и D(p) не имеют общих корней (взаимно просты). Тогда исходная дроь может быть представлена в виде суммы элементарных дробей, соответствующих корням pk кратности mk многочлена D(p) следующим образом:
Для нахождения коэффициентов bkj существует несколько методов. Мы рассмотрим метод неопределенных коэффициентов. Надо умножить обе части вышеприведенного равенства на D(p) и
30 Напомним, что периодическая функция представляется рядом Фурье, который представляет из себя сумму не более чем счетного числа синусов и косинусов разного периода, а непериодическая функция представляется интегралом Фурье, где период у подынтегральных тригонометрических функций меняется непрерывно.
31 Рациональная дробь называется правильной, если степень ее числителя меньше степени знаменателя.
приравнять коэффициенты при одинаковых степенях p в обеих частях. В результате получится система линейных уравнений, которую надо разрешить относительно b kj. Рассмотрим дробь 1/((p+1)*(2p+1). Применительно к нашему случаю получаем: 1=b1(2p+1)+b2(p+1). Отсюда также получаем следующую систему линейных уравнений:
2b1+b2=0 b1+b2=1.
Эта система имеет следующее решение: b1= - 1, b2=2. Таким образом, мы можем записать v1* ( p) = 10(2 p2+1 − p1+1) −10e−2 p ( 2 p2+1 − p1+1).
Как следует из более раннего v1(t)=10*(f(t)-f(t-2)), где
материала, 2/(2p+1)↔2(1-e-t/2), 1/(p+1)↔(1-e-t). Таким образом,
Помимо того, что знание передаточной функции системы дает возможность найти решение основной задачи исследования динамических свойств - построения семейства траекторий, при помощи передаточной функции оказывается также возможным исследовать ряд вопросов устойчивости и точности линейных динамических систем. Известно, что для устойчивости системы необходимо, чтобы корни знаменателя передаточной функции имели отрицательные действительные части или, в постановке (1), чтобы действительные части собственных значений матрицы А были отрицательны. В этом случае можно показать, что свободный отклик системы дифференциальных уравнений (1) будет стремится к нулю с ростом времени [ 3].
В соответствии с известной в операционном исчислении теоремой о предельном значении, установившееся значение выхода совпадает со значением в нуле изображения выхода, т.е. vуст=K(0)uуст, где vуст и uуст есть v*(0) и u*(0) соответственно. При исследовании точности системы в качестве u рассматривается возмущающее воздействие. Устранение установившегося отклонения можно достичь “обнулением” K(0). Есть два пути реализации этого- введение в обратную связь интегрирующего звена и введение компенсирующего воздействия по возмущению [3].
Комплексное число К(iω) называют комплексным коэффициентом усиления, а его абсолютную величину A(ω) = |К(iω)|- амплитудной характеристикой системы. Она показывает, во сколько раз увеличивается или уменьшается амплитуда синусоидального входного сигнала с частотой ω. Некоторые системы резко уменьшают амплитуды сигналов, частоты которых принадлежат определенной полосе. В этом случае говорят, что система не пропускает сигналов (возмущений), соответствующих этим частотам.
В качестве примера рассмотрим инерционное звено. Его передаточная функция K(p)=1/(Тр+1). Комплексный коэффициент усиления K(iω)=1/(1+iTω)=(1-iωT)/(1+ω2T 2). Амплитудная характеристика А(ω ) = |K(iω)|=√[(1+ω2T2)/(1+ω2T2)2]= 1/√(1+T2ω2). Отсюда видно,что чем больше частота,тем меньшеамплитуда выходного сигнала. Инерционное звено не пропускает высокочастотных возмущений, т. е. возмущений, имеющих малый период повторяемости. К этой категории относятся обычно мелкие
T dvdt + v = u,
T ( pv *−pv(−0))+ v*= u*, v*=(u *+Tpv(−0)) Tp1+1, неполадки, возникающие в процессе производства.
Выше начальные условия принимались нулевыми. Как быть, если это не так? Рассмотрим конкретный пример.
Но это соответствует следующему соединению:
Рис. 14
Таким образом, для учета ненулевых начальных условий можно добавить дополнительные входные постоянные воздействия, пропущенные через дополнительные звенья. Посмотрим теперь, что может означать в изображении выхода дополнительное слагаемое
Перейдя к оригиналу мы получаем следующую добавку к выходному сигналу:
Но эта добавка, первоначальная величина которой определяется начальным состоянием v(-0) быстро убывает (экспоненциально) с ростом времени. Это подтверждает сделанное выше высказывание, что в устойчивой системе (таковым является и инерционное звено) с ростом времени быстро пропадает зависимость от начального состояния.
2) Дискретные динамические системы
Ранее уже говорилось об аналогии в описании и анализе динамических систем в непрерывном и дискретном времени. В частности, стационарные линейные системы в дискретном времени описываются системой разностных уравнений вида:
сначальными условиямиvr(0)= cr.
Подстановкой легко убедиться, что решение соответствующей однородной системы (т.е. когда Bu(t)=0,
i =0
На основе полученного решения можно рассчитать траекторию системы32. Кроме того, оно позволяет нам решить вопрос относительно устойчивости системы. Как говорилось выше, решение неоднородной системы уравнений складывается из свободного отклика (в данном случае Atv(0)) и вынужденного отклика, конкретный вид которого определяется управляющим воздействием. Можно показать, что если собственные значения матрицы А или, что то же самое, корни λ1,…,λn ее характеристического полинома |A-λI|, лежат внутри единичного шара, то с ростом t матрица At стремится к нулевой матрице (аналогично членам геометрической прогрессии), т.е. при больших t влияние начального состояния становится пренебрежимо малым. Это говорит о том, что система является устойчивой.
Выше говорилось, что систему дифференциальных уравнений высокого порядка можно привести к системе первого порядка вида (1). Аналогично можно систему разностных уравнений высокого порядка свести к системе уравнений первого порядка вида (5). Это обеспечивает единообразие в формулировке задачи и получения ее решения. Однако, в том простом случае, который мы рассмотрим ниже, нам удобнее будет работать с системой высокого порядка. Ниже будут рассматриваться только конечно-разностные уравнения вида vt=a1vt-1+a2vt-2+ u(t),
т. е. линейные конечно-разностные уравнения второго порядка. Они называются однородными, если u(t) = 0 при любых t, неоднородными — в противном случае.
32 Также как и линейные системы с непрерывным временем линейные системы с дискретным временем можно исследовать с помощью изображений. Соответствующее преобразование для перехода к изображениям называется z-преобразованием.
Рассмотрим возникающие при этом случаи.
а) D > 0. Характеристическое уравнение имеет два различных вещественных корня. Решение описывается равенством (10); если оба корня положительны, то обе компоненты решения — монотонные геометрические прогрессии. Если имеются отрицательные корни, то каждому из них отвечает знакочередующаяся составляющая решения (10).
б) D =0. Характеристическое уравнение имеет совпадающие вещественные корни, и решение имеет вид (11). в) D <0. Характеристическое уравнение имеет пару сопряженных комплексных корней: λ1,2=α ± iβ.
Равенство (10) при этом справедливо. Рассмотрим представление корней в тригонометрической (экспоненциальной) форме:
λ1,2= ρ(cosω ± i sinω)= ρe±iω ,
гдеρ = λ1= λ2=
Подставляя эти корни в (10), получим:
33 Покажем , что в левой части уравнения стоит характеристический полином |A-λI|. Действительно, используем обозначение v1(t)=vt и подстановку v2(t)=v1(t-1), которую также используем в качестве дополнительного уравнения. Тогда систему разностных уравнений второго порядка можно представить следующей системой разностных уравнений первого порядка:
Т.о. корни рассматриваемого характеристического уравнения являются собственными значениями матрицы А.
vt = ρt (A1eiωt + A2e−iωt )= ρt ((A1+ A2)cosωt +i(A1− A2)sinωt).
Поскольку, как не трудно убедиться, и действительная и мнимая части полученного решения удовлетворяют системе (8), а нас интересует лишь действительное решение, то линейная комбинация действительной и мнимой частей (действительная), также будет решением:
где B1 и B2 — постоянные, для определения которых как раз достаточно начальных условий v(0) и v(1). Таким образом, при D < 0 решение носит характер колебаний, амплитуда которых возрастает (при ρ > l) или убывает (при ρ < l); если частота выражена в радианах, то период колебаний Т = 2π/ω. На рисунке парабола АОВ, описываемая уравнением a12+4a2=0, соответствует случаю D=0.
Выше параболы располагается область, соответствующая случаю D > 0, ниже — случаю D <0. Решение называется устойчивым, если vt —> 0 при t —> ∞; в противном случае оно называется неустойчивым. Равенства (10) и (11) показывают, что решение будет устойчивым в том и только том случае, если оба корня характеристического уравнения по модулю меньше единицы. В случае D=0(на параболе)характеристическое уравнение имеет лишь кратный кореньa1/2,поэтому условием устойчивости является |a1|<2. В случае D < 0(ниже параболы)условию устойчивости соответствуетρ<1,так какρ=|λ1| =|λ2|=√(λ1λ2) и по теореме Виета это равно √(-a2), то необходимым и достаточным условием устойчивости является
⇒ a2<1−| a1| & | a1|<2. Мы получили область над параболой и ограниченную треугольником АСВ. Убедимся, что последние полученные условия являются также и достаточными:
Подводя итог анализа устойчивости для всех 3-х случаев (D=0, D<0, D>0), следует сказать, что при выполнении условий (14), которым отвечают внутренние точки треугольника АСВ, система устойчива. Справедливо и обратное утверждение.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|



 характеристического уравнения (9).
характеристического уравнения (9).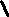 λ1λ2=
λ1λ2= 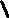 α2+ β 2;tg ω = αβ .
α2+ β 2;tg ω = αβ .

 Это справедливо, если и только если взять наиболее ограничивающее из полученных неравенств, т.е. ⇔
Это справедливо, если и только если взять наиболее ограничивающее из полученных неравенств, т.е. ⇔ a12+4a2<2−| a1|,⇔ a12+4a2<4−4 | a1|+a12
a12+4a2<2−| a1|,⇔ a12+4a2<4−4 | a1|+a12
 Полученным необходимым и достаточным условиям отвечают точки внутри треугольника АСВ на рисунке. Это множество можно описать и с помощью следующего двойного неравенства:
Полученным необходимым и достаточным условиям отвечают точки внутри треугольника АСВ на рисунке. Это множество можно описать и с помощью следующего двойного неравенства: