|
|
Сопряжение дуги и прямой дугой окружности заданного радиусаМогут встретиться два случая такого сопряжения: внешнее касание сопрягающей дуги с заданной и внутреннее касание. В обоих случаях задача сводится к определению центра сопрягающей дуги и точек касания. При внешнем касании (рисунок 52, а) из центра заданной дуги – точки O1 проводят вспомогательную дугу радиусом R + Rс. На расстоянии, равном радиусу Rc сопрягающей дуги, параллельно заданной прямой проводят прямую. Точка О пересечения вспомогательной дуги и прямой есть центр сопрягающей дуги. На пересечении прямой, соединяющей точки О и O1 с заданной дугой, отмечают точку касания A. Вторую точку касания В определяют как точку пересечения заданной прямой с перпендикуляром, опущенным на нее из точки О. При внутреннем касании (рисунок 52, б) определение центра сопрягающей дуги и точек касания аналогичны предыдущему случаю с той лишь разницей, что радиус вспомогательной дуги равен Rc – R.
а б
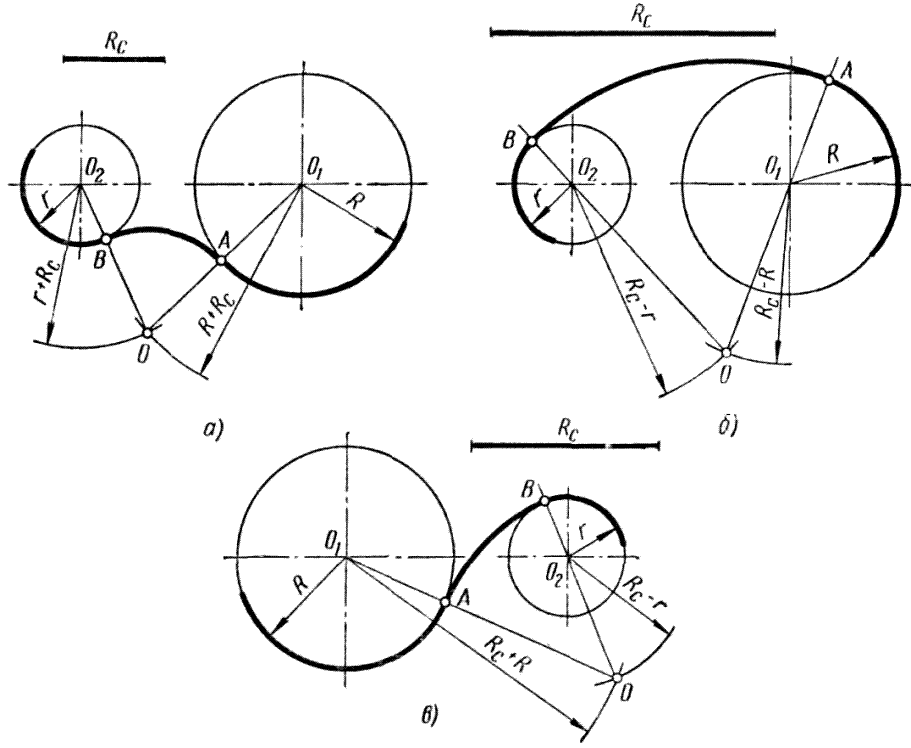
Рисунок 52 Сопряжение двух дуг дугой окружности заданного радиуса Различают три вида такого сопряжения: 1) внешнее сопряжение при внешнем касании сопрягающей дуги с двумя заданными; 2) внутреннее сопряжение при внутреннем касании сопрягающей дуги с двумя заданными; 3) смешанное сопряжение при внешнем касании сопрягающей дуги с одной заданной и внутреннем касании с другой. При внешнем сопряжении (рисунок 53, а) центр сопрягающей дуги точка O располагается в точке пересечения вспомогательных дуг радиусами r + Rc и R + Rc, проведенных соответственно из центров сопрягаемых дуг – точек O2 и O1. Точки касания A и B определяются как точки пересечения заданных дуг с прямыми OO1 и OO2. Внутреннее сопряжение дуг радиусами r и R дугой радиусом Rc показано на рисунке 53, б. Для определения центра сопрягающей дуги – точки О проводят вспомогательные дуги радиусами Rc – r и Rc – R соответственно из центров заданных дуг – точек O2 и O1. Точка О пересечения этих дуг и явится центром сопрягающей дуги. Из точки О через точки O1 и O2 проводят прямые до пересечения с заданными дугами и получают соответственно две точки касания – A и B.
Рисунок 53
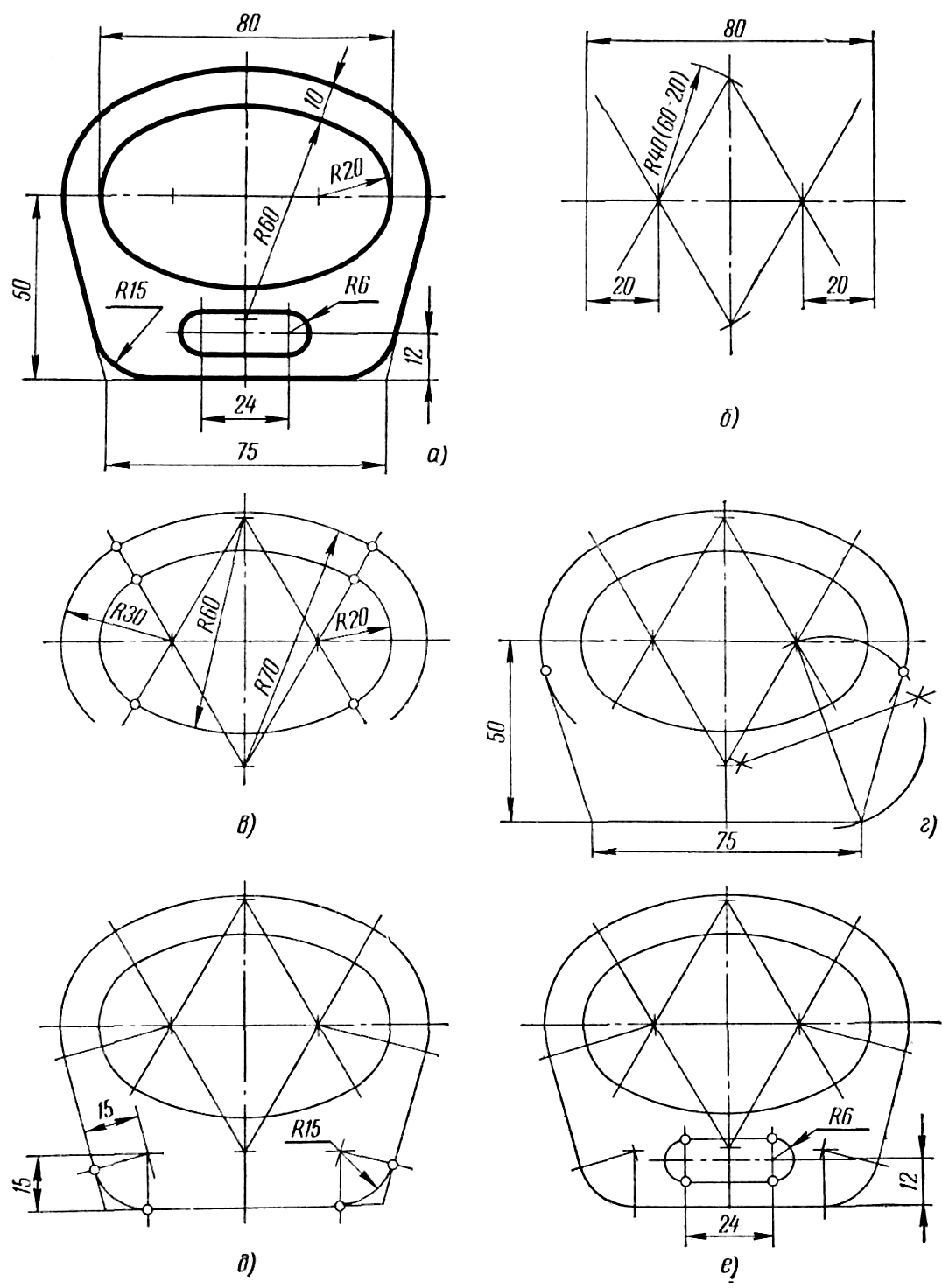
При смешанном сопряжении центр сопрягающей дуги – точка О определяется как точка пересечения двух вспомогательных дуг радиусами Rc+R и Rс – r (рисунок 53, в) или Rс – R и Rс + r, проведенных соответственно из центров заданных дуг – точек O1 и O2. Для определения точек касания сопрягающей дуги с заданными проводят две прямые: одну через точки О и O1, другую через точки О и O2. Точки пересечения каждой из них с заданными дугами дают искомые точки касания A и B. Вычерчивание контуров деталей Последовательность вычерчивания контуров деталей в основном зависит от их формы. Поэтому можно указать только на некоторые общие положения, справедливые для всех случаев. Перед вычерчиванием любого контура необходимо установить, из каких линий и их сочетаний он состоит, а также решить, какие геометрические построения следует выполнить при вычерчивании контура. Только после подобного анализа можно приступать к построению контура. Последовательность вычерчивания контура проследим на примере контура скобы (рисунок 54, а). Вычерчивание начинают с проведения осей симметрии (вертикальная ось на рисунке 54, б), осевой (горизонтальная ось на рисунке 54, б) и центровых линий контура. Затем проводят линии, связанные с горизонтальной осью (рисунок 54, в), и строят остальные основные линии контура (рисунок 54, г). Далее выполняют скругления углов (рисунок 54, д) и вычерчивают внутренние очертания, не связанные с другими линиями (прорезь, рисунок 54, е). Последними вычерчивают контуры, не содержащие элементов сопряжения. Заканчивают построение проведением выносных и размерных линий с простановкой размеров (рисунок 54, а).
Рисунок 54 Архитектурные обломы Многие здания снаружи и внутри имеют различные архитектурные украшения. Профиль архитектурных украшений складывается из элементов, называемых архитектурными обломами. Архитектурные обломы украшают не только здания. Их можно увидеть в контуре постаментов, декоративных ваз, мебели и т. п. По форме архитектурные обломы могут быть прямолинейные (рису-нок 55) и криволинейные (рисунки 56, 57). Криволинейные обломы, такие как полувал, шейка, прямой и обратный четвертной вал, прямая и обратная выкружка (рисунок 56), очерчены при помощи одной дуги, и способ их построения понятен из чертежа. Более сложные криволинейные обломы состоят из двух дуг. К ним относятся: гусёк прямой и обратный, каблучок прямой и обратный, скоция, сложный торус (рисунок 57).
Рисунок 55 Рисунок 56
В построении гуська и каблучка много общего. Для построения, например, прямого гуська (рисунок 57, а) заданные точки А и В соединяют прямой линией. Отрезок AB делят пополам в точке С. Радиусом R = AC =CB из точек А, С и В проводят дуги до взаимного пересечения в точках O1 и O2 , и из них тем же радиусом R описывают две дуги, являющиеся профилем прямого гуська. Вычерчивание обратного гуська или одного из видов каблучка аналогично вычерчиванию прямого гуська, при этом меняется только положение центров O1 и O2 (рисунок 57, б, в, г). Сложный торус строят по заданному радиусу R (рисунок 57, д). Проводят прямую и на ней отмечают два центра – O1 и O2 на расстоянии 2R. Из центра O1 описывают четверть окружности радиусом R, а из центра O2 – радиусом 3R. Для построения скоции также задают радиус R (рисунок 57, е) и строят шесть квадратов со сторонами, равными заданному радиусу. Наметив точки O1 и O2, описывают две дуги радиусами R и 2R.
Рисунок 57 ПЛОСКИЕ КРИВЫЕ Кривые, у которых все точки расположены в одной плоскости, называют плоскими. Часть плоских кривых, состоящих из дуг окружностей, образует группу циркульных кривых. Дуги циркульных кривых касаются друг друга, поэтому построение их основано на правилах сопряжения и выполняется при помощи циркуля. Другая часть плоских кривых, которые нельзя построить с помощью циркуля, относится к группе лекальных кривых. Лекальные кривые строят по точкам, зная закон их образования, а обводят по лекалу. ЦИРКУЛЬНЫЕ КРИВЫЕ Завитки Спиральная кривая, вычерченная циркулем путем сопряжения дуг окружностей различных радиусов, называется завитком. На рисунке 58, а показано построение двуцентрового завитка. Он состоит из ряда полуокружностей, описанных попеременно из заданных центров O1 и O2. Точки касания проводимых дуг расположены на прямой, соединяющей эти центры. Первую полуокружность описывают радиусом R, равным расстоянию между центрами O1 и O2. Радиус каждой последующей полуокружности увеличивают на величину первоначального радиуса R. Таким образом, вторую полуокружность описывают радиусом 2R, третью - радиусом 3R и т. д.
а б Рисунок 58
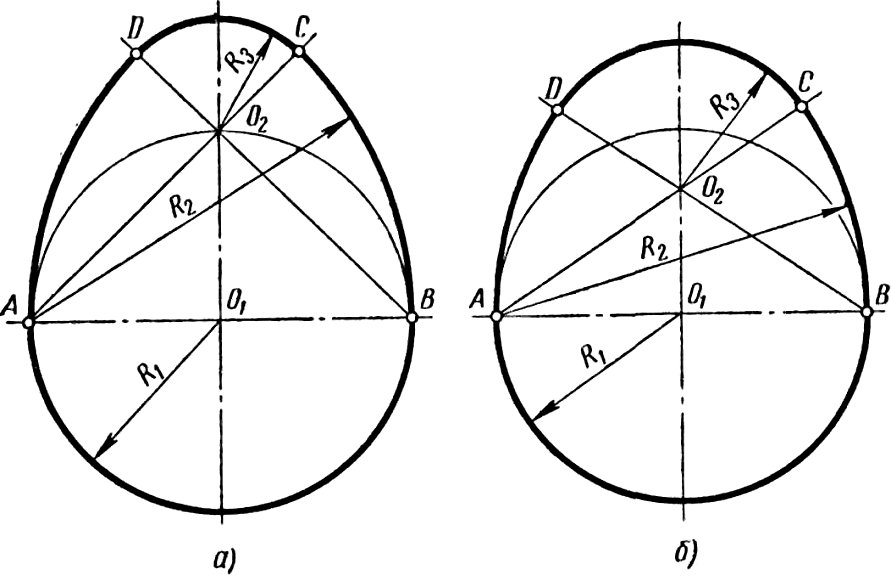
Построение трехцентрового завитка по заданным центрам O1, O2 и O3, расположенных в вершинах равностороннего треугольника, приведено на рисунке 58, б. Через каждую пару центров проводят прямую линию. Из центра O1 описывают дугу радиусом R = O1O3 в пределах между точками O3 и 1. Следующую дугу радиусом 2R проводят из центра O2 до точки 2. Затем описывают дугу радиусом 3R из центра O3. Дуга, проведенная снова из центра O1, имеет радиус 4R и т. д. Завитки четырехцентровые, пятицентровые и т. д. строят таким же образом. Коробовые кривые Коробовой кривой называется односторонне выпуклая циркульная кривая (замкнутая или незамкнутая), образуемая сопряжением дуг: окружностей. Существует несколько разновидностей коробовых кривых. Овал – замкнутая коробовая кривая, имеющая две оси симметрии. Элементами, определяющими размер овала, являются его длина и ширина, измеряемые по осям симметрии. Построение овала по его длине AB и ширине CD показано на рисун-ке 59. Вначале проводят две взаимно перпендикулярные прямые, пересекающиеся в точке О (рисунок 59, а). На горизонтальной прямой в обе стороны от точки О откладывают отрезок
а б
Рисунок 59 Овоид – замкнутая коробовая кривая, имеющая одну ось симметрии. Построение овоида по его ширине – отрезку AB приведено на рисунке 60, а. Через середину отрезка AB – точку O1 проводят прямую, перпендикулярную к нему. Из точки O1 описывают окружность радиусом Если точку O2 расположить ближе к точке O1 или дальше от нее, то овоид получится соответственно более тупым или более острым. Для построения тупого овоида задают его ширину AB и расстояние между центрами O1O2 (рисунок 60 б). Порядок построения остается прежним.
а б
Рисунок 60
Коробовые кривые сводов относятся к незамкнутым коробовым кривым. Они находят применение при строительстве сводов и арок мостов, входов в здания, различных перекрытий, например метро и т. п. Ниже разобрано построение коробовых кривых пологого, крутого и ползучего сводов. Построение коробовой кривой пологого свода по его ширинеАВи высотеОС (рисунок 61). На горизонтальной прямой откладывают ширину свода – отрезок AB и через его середину точку О проводят прямую, перпендикулярную к нему. На этой прямой от точки О откладывают высоту свода – отрезок OC. Из точки О радиусом OA описывают дугу AE и на ней отмечают точку D с помощью того же радиуса OA, но с центром в точке А. Точку D соединяют прямыми с точками А, Е и О. Затем через точку С проводят прямую CF || DE до пересечения ее с прямой AD в точке F. Через точку F проводят прямую FO2 || DO до пересечения ее с отрезком AB в точке O1, а с прямой OC в точке O2. Точку O3 получают при помощи дуги радиусом OO1. Полученные точки O1, O2 и O3 являются центрами дуг, из которых состоит данная кривая. Радиусом R1 = O3B описывают дуги из центров O1 и O3, а радиусом R2 = O2C – дугу из центра O2.
Рисунок 61
Построение коробовой кривой крутого свода по ширине AB и высоте ОС (рисунок 62). Отрезок AB делят пополам, строят прямоугольник АЕСО и проводят в нем диагональ AC. Углы EAC и ECA делят пополам. На пересечении биссектрис этих углов получают точку D и из нее опускают перпендикуляр на диагональ AC. Перпендикуляр продолжают до пересечения с отрезками: OC в точке O1 и AB в точке O2. Точку O3 получают при помощи дуги радиусом OO2. Точки O1, O2 и O3 являются центрами дуг радиусами R1 и R2, с помощью которых строят контур кривой.
Рисунок 62 Построение коробовой кривой ползучего свода по его ширине АВ и прямой CD, касательной к вершине свода (рисунок 63). Строят отрезок AB, представляющий ширину свода, и прямую CD (ее называют замковой прямой). Из точек A и В восставляют к отрезку AB перпендикуляры и продолжают их до пересечения с прямой CD в точках М и N. На прямой CD откладывают отрезок EM = AM. Из полученной точки Е – вершины свода восставляют перпендикуляр к прямой CD и на пересечении его с отрезком AB отмечают точку O1. На прямой BN откладывают от точки N отрезок FN=EN. Из точки F проводят прямую, параллельную отрезку AB, до пересечения с прямой EO1 в точке O2. В точках O1 и O2 находятся центры дуг R1 = O1A и R2 = O2F, определяющих контур ползучего свода.
Рисунок 63
ЛЕКАЛЬНЫЕ КРИВЫЕ Лекальные кривые – это такие кривые, которые могут быть вычерчены только с помощью лекала по предварительно построенным точкам. Лекальные кривые широко применяются в очертаниях различных деталей и предметов. Это могут быть профили зубчатых колес и кулачков, очертания кронштейнов, подвесок, посуды и мебели. Лекальные кривые могут быть также получены в результате сечения цилиндра, конуса и других тел вращения плоскостью. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|




 , а на вертикальной –
, а на вертикальной –  . Точки A и С соединяют прямой линией, и из точки О описывают дугу радиусом OA до пересечения ее с прямой CD в точке E. На прямой AC откладывают отрезок CF=CE и получают точку F. Через середину отрезка AF проводят перпендикуляр и на пересечении его с прямыми AB и CD получают точки O1 и O2. На прямых AB и CD строят точки O3 и O4, симметричные точкам O1 и O2 относительно центра О (рисунок 59 б). Точки O1, O2,O3, O4 являются центрами сопрягаемых дуг, определяющих контур овала, а точки касания дуг располагаются на прямых O1O2, O3O2, O1O4 и O3O4. Из центров O1 и O3 описывают дуги радиусом R1 = O1A, а из центров O2 и O4 – дуги радиусом R2 = O2C и получают контур овала.
. Точки A и С соединяют прямой линией, и из точки О описывают дугу радиусом OA до пересечения ее с прямой CD в точке E. На прямой AC откладывают отрезок CF=CE и получают точку F. Через середину отрезка AF проводят перпендикуляр и на пересечении его с прямыми AB и CD получают точки O1 и O2. На прямых AB и CD строят точки O3 и O4, симметричные точкам O1 и O2 относительно центра О (рисунок 59 б). Точки O1, O2,O3, O4 являются центрами сопрягаемых дуг, определяющих контур овала, а точки касания дуг располагаются на прямых O1O2, O3O2, O1O4 и O3O4. Из центров O1 и O3 описывают дуги радиусом R1 = O1A, а из центров O2 и O4 – дуги радиусом R2 = O2C и получают контур овала.
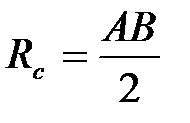 и на пересечении ее с перпендикуляром получают точку O2. Далее проводят прямые AO2 и BO2 и продолжают их за точку O2. Из точек A и В радиусом R2 = AB описывают две дуги до пересечения их в точках C и D с проведенными прямыми. Последнюю дугу радиусом R3 = O2C описывают из точки O2.
и на пересечении ее с перпендикуляром получают точку O2. Далее проводят прямые AO2 и BO2 и продолжают их за точку O2. Из точек A и В радиусом R2 = AB описывают две дуги до пересечения их в точках C и D с проведенными прямыми. Последнюю дугу радиусом R3 = O2C описывают из точки O2.