
|
|
Уравнение прямой в пространстве по точке иАналитическая геометрия Уравнение поверхности в пространстве Любое уравнение, связывающее координаты x, y, z любой точки поверхности является уравнением этой поверхности. Общее уравнение плоскости Плоскостьюназывается поверхность, координаты всех точек которой удовлетворяют общему уравнению: Ax + By + Cz + D = 0, где А, В, С – координаты вектора
Возможны частные случаи: например, А = 0 – плоскость параллельна оси Ох D = 0 – плоскость проходит через начало координат А = В = 0 – плоскость параллельна плоскости хОу А = D = 0 – плоскость проходит через ось Ох А = В = D = 0 – плоскость совпадает с плоскостью хОу
Уравнение плоскости, проходящей через три точки Известно, три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Рассмотрим точки М1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3) плоскости в декартовой прямоугольной системе координат, не лежащие на одной прямой. Возьмем произвольную точку М(x, y, z) плоскости и составим векторы (
Таким образом,
Уравнение плоскости, проходящей через три точки:
Уравнение плоскости по точке и вектору нормали
Если в пространстве задана точка М0(х0, у0, z0), то уравнение плоскости, проходящей через точку М0 перпендикулярно вектору нормали
A(x – x0) + B(y – y0) + C(z – z0) = 0.
Действительно,для произвольной точки М(х, у, z), принадлежащей плоскости, составим вектор
Таким образом, получаем уравнение плоскости
Уравнение плоскости в отрезках Если в общем уравнении Ах + Ву + Сz + D = 0 поделить обе части на -D
заменив
Числа a, b, c являются точками пересечения плоскости соответственно с осями х, у, z. Расстояние от точки до плоскости Расстояние от произвольной точки М0(х0, у0, z0) до плоскости Ах+Ву+Сz+D=0 равно:
Угол между плоскостями
j1 j 0
Угол между двумя плоскостями в пространстве j связан с углом между нормалями к этим плоскостям j1 соотношением: j = j1 или j = 1800 - j1, т.е. cosj = ±cosj1. Определим угол j1. Известно, что плоскости могут быть заданы соотношениями:
Таким образом, угол между плоскостями находится по формуле:
Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.
Условия параллельности и перпендикулярности плоскостей На основе полученной выше формулы для нахождения угла между плоскостями можно найти условия параллельности и перпендикулярности плоскостей. Для того чтобы плоскости были перпендикулярны необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если:
Плоскости параллельны, тогда векторы нормалей коллинеарны:
Уравнение линии в пространстве Любая линия в пространстве может быть определена как совокупность точек, координаты которых в некоторой выбранной в пространстве системе координат удовлетворяют уравнению:
F(x, y, z) = 0. Это уравнение называется уравнением линии в пространстве. Кроме того, линия в пространстве может быть определена и иначе. Ее можно рассматривать как линию пересечения двух поверхностей, каждая из которых задана каким- либо уравнением. Пусть F(x, y, z) = 0 и Ф(x, y, z) = 0 – уравнения поверхностей, пересекающихся по линии L. Тогда пару уравнений
назовем уравнением линии в пространстве.
Уравнение прямой в пространстве по точке и направляющему вектору Возьмем произвольную прямую и вектор На прямой возьмем две произвольные точки М0(x0, y0, z0) и M(x, y, z).
M0
0 y
x
Обозначим радиус-векторы этих точек как Т.к. векторы Итого, можно записать: Т.к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – параметрическое уравнение прямой. Это векторное уравнение может быть представлено в координатной форме:
Преобразовав эту систему и приравняв значения параметра t, получаем канонические уравнения прямой в пространстве. Исключим параметр Т.к.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 – вектор нормали к плоскости.
– вектор нормали к плоскости. . Тогда векторы компланарны и их смешанное произведение равно нулю:
. Тогда векторы компланарны и их смешанное произведение равно нулю:
 .
. (A, B, C), имеет вид:
(A, B, C), имеет вид: . Т.к. вектор
. Т.к. вектор  . Тогда скалярное произведение
. Тогда скалярное произведение .
. ,
, , получим уравнение плоскости в отрезках:
, получим уравнение плоскости в отрезках: .
.


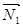
 , где
, где (x, y, z). Угол между векторами нормали найдем из их скалярного произведения:
(x, y, z). Угол между векторами нормали найдем из их скалярного произведения: .
.
 .
. .
.
 (m, n, p), параллельный данной прямой. Вектор
(m, n, p), параллельный данной прямой. Вектор  z
z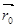


 – канонические уравнения прямой.
– канонические уравнения прямой.