|
|
Алгоритм выявления фиктивной переменной- Для переменной x1 сравниваются половины столбца значений функции: верхняя и нижняя, так как именно в верхней половине x1 = 0, а нижней x1 = 1; если они совпадают, то переменная x1 фиктивная; - для переменной x2 сравниваются четвертины столбца в каждой половине, так как именно в верхних четвертинах x2 = 0, а в нижних x2 = 1; если четвертины в каждой половине совпадаю, то переменная x2 фиктивная; - и так далее (за четвертинами следуют 1/8, 1/16, …). Достаточное условие отсутствия фиктивных переменных.Если вес вектора – столбца значений функции нечетен, то функция не может содержать фиктивных переменных. Алгоритм удаления фиктивной переменной xi состоит в вычеркивании из таблицы истинности всех строк, в которых xi = 0 (или всех строк, в которых xi = 1), и столбца xi . Пример.После удаления фиктивной переменной x3 имеем
10. Формула как способ задания функции. Равносильные формулы. Основные равносильности Пусть даны Ф — множество символов функций и Х — множество символов переменных. База индукции. Если fi - символ n-местной функции из множества Ф, а x1, x2, ... , xn - переменные из множество Х, то последовательность символов fi (x1, x2, ... , xn) - формула над Ф и Х. Индуктивный переход. Если fj - символ m-местной функции из Ф, а A1, A2, ... , Am — переменные из Х или формулы, то последовательность символов fj(A1, A2, ... , An) - формула над Ф и Х, а A1, A2, ... , Am – ее подформулы. Других формул нет. Способ записи формул для элементарных булевых функций: c Ù a, b¯ c , `a и т.д. Формула задает функцию, а функция реализует формулу. Пример. ( a Å ( c Ù`a ) ) Ú ( b ¯ c). или, если опустить скобки, то формула примет вид: a Å c`a Ú ( b ¯ c). Равносильность формул Определение.Две формулы F' и F" называются равносильными, если они задают равные функции. В этом случае пишут F' = F". Доказывать равносильности можно с помощью таблиц истинности или рассуждений, опирающихся на свойства элементарных булевых функций. Пример.Докажем равносильность
Основные равносильности К основным относят следующие равносильности, которые рекомендуется запомнить и применять при упрощении формул.
11) Формула Шенона.Докозательство Определение. Разложением Шеннона называется следующее разложение булевой функции f(x1, ...,xn) по переменной xi:
Доказательство(не умоляя общности, для i =1). Покажем, что формула верна в обоих случаях: для x1 = 0 и x1 = 1. Если x1 = 0, то f (0, x2, ... , xn) = 0 f (1, x2, ... , xn) Ú 1 f (0, x2, ... , xn) = = f (0, x2, ... , xn). Если x1 = 1, то f (1, x2, ... , xn) =1 f (1, x2, ... , xn) Ú 0 f (1, x2, ... , xn) == f (0, x2, ... , xn). О пределение. Сомножитель f (x1, ..., xi -1, 1, xi+1,... , xn) в формуле Шеннона называется коэффициентом разложения функции f (x1, x2, ... , xn) по переменной xi при xi, а сомножитель f (x1, ..., xi -1, 0, xi+1,... , xn) — коэффициентом разложения функции f (x1, x2, ... , xn) по xi при Пример.Функцию
12) Разложение функции по k переменным. Доказательство Разложим функцию f(x1, ...,xn) последовательно по двум переменным: сначала саму функцию по переменной x1, затем коэффициенты разложения по переменной x2. Рассмотрим булеву функцию f (x1, x2, ... , xn) и, используя формулу Шеннона, последовательно разложим функцию - по первой переменной, - по двум первым переменным, - по k первым переменным. 1. Разложим функцию по первой переменной: f (x1, x2, ... , xn) = x1 f (1, x2, ... , xn) Ú `x1 f ( 0, x2, ... , xn). 2. Разложим в полученной формуле оба коэффициента разложения по второй переменной: f (x1, x2, ... , xn) = x1 f (1, x2, ... , xn) Ú `x1 f ( 0, x2, ... , xn) = = x1 [ x2 f (1,1, x3, ... , xn) Ú`x2 f (1,0, x3, ... , xn) ] Ú Ú`x1 [ x2 f (0,1, x3, ... , xn) Ú`x2 f (0,0, x3, ... , xn) ] = = x1 x2 f (1,1, x3, ... , xn) Ú x1`x2 f (1,0, x3, ... , xn) Ú Ú`x1 x2 f (0,1, x3, ... , xn) Ú`x1`x2 f (0,0, x3, ... , xn) = [ свернем последнюю формулу в более короткую, используя следующие обозначения: x = x1 и `x = x0, то есть xс, где c Î {0,1}, и условимся читать символы xс как “x в степнени c “]
3. По аналогии с предыдущей формулой запишем формулу разложения функции по k переменным: Доказательство.Подставим в левую и правую части равенства произвольный набор a1 a2 ... an:
Упростим правую часть, рассуждая следующим образом. Нетрудно проверить, что
13) Получение СовДНФ из разложения функции по переменным. Утверждение о существовании и единственности СовДНФ.Алгоритм построения СовДНФ по таблице истинности функции. Применив формулу разложения булевой функции f (x1, x2, ... , xn) по k переменным при k = n, получим:
Поскольку коэффициентами разложения f (c1, c2, ... , cn) в этой формуле являются значения функции f (x1, x2, ... , xn) на всевозможных наборах c1 c2 ... cn, то возможны два случая: - если набор c1 c2 ... cn Î M0 ( f ), то f (c1, c2, ... , cn ) = 0 и поэтому обращается в 0 соответствующее слагаемое правой части; - если набор c1 c2 ...cn Î M1 ( f ), то f(c1, c2, ... , cn ) = 1 и слагаемое упрощается. В результате имеем формулу разложения функции по всем переменным:
Определение.Совершенная дизъюнктивная нормальная форма булевой функции
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
, построив таблицы истинности для левой и правой формул.
.
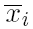разложим по переменной x:
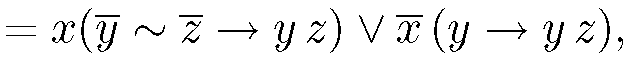
и докажем, что данное разложение верно.
1, если и только если ai = ci (в самом деле: 0 0 = 1, 11 = 1, но 0 1 = 0 и 10 = 0), поэтому конъюнкция 
равна единице лишь в единственном случае, когда наборы a1 a2 ... ak и с1 с2 ... сk совпадают. А это значит, что она не обращает в ноль лишь одно слагаемое правой части — то, для которого a1 a2 ... ak = с1 с2 ... сk и в котором сама обращается в единицу. Подставив в ставшееся слагаемое a1 a2 ... ak вместо с1 с2 ... сk , получим
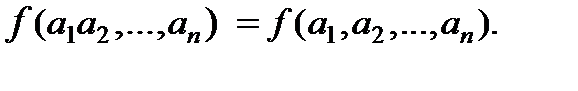
, или СовДНФ, — это формула вида: