
|
|
Утверждение о соседних интервалахДва соседних интервала ранга r (размерности s) не пересекаются, а их объединение образует интервал ранга r -1 (размерности s +1). Доказательство. Соседние интервалы I1 и I2 не пересекаются, как так их ортогональная компонента во всех векторах одного интервала равна 0, а в векторах другого равна 1. Мощность объединения таких интервалов равна сумме их мощностей: / I / = / I1 È I2 / = / I1 / + / I2 / = 2s + 2s = 2s+1, т.е. она оказывается целой степенью двойки (s+1-й). Количество компонент в векторах множества I , претендующих быть внутренними, тоже равно s +1, так как к s внутренним компонентам интервалов I1 и I2 добавляется еще одна, ортогональная, компонента. Это равенство означает, согласно рассмотренному ранее алгоритму, что множество I образует интервал размерности s +1 (ранга r -1, так как r + s = n ). Определение.Операцию объединения двух интервалов I1 и I2, соседних по i – й компоненте, назовем склеиванием интервалов i-ой компоненте, а результат их склеивания I = I1 È I2 - расширением каждого из интервалов I1 и I2 по i – й компоненте. Пример.Соседние интервалы Очевидно, что на матрице в коде Грея соседние по i-й компоненте интервалы располагаются симметрично относительно оси симметрии этой компоненты.
6. Алгоритм распознавания интервала, заданного перечислением векторов. Задано множество A булевых векторов длины n. Требуется определить, образует ли множество A интервал и, если образует, найти его границы: a, b. Шаг 1: если мощность множества A не является целой степенью двойки, т.е. |A| ¹ 2c, где c — целое, то A — не интервал, идем на конец. Шаг 2: Считаем число s несовпадающих компонент в векторах множества A, т.е. число компонент, претендующих быть внутренними; Если s ¹ c, то A - не интервал, идем на конец; иначе A - интервал, s - его размерность, r=n-s - ранг; Шаг 3: Находим границы интервала a и b Вектор минимального веса (из всех векторов множества A) является наименьшим элементом интервала (a), а вектор максимального веса — его наибольшим элементом (b), т.е. a и b - границы интервала. Конец. Примеры. А = {010, 011, 001}: множество не образует интервал, так как его мощность, равная 3, целой степенью двойки не является. А = {010, 011, 001}: множество не образует интервал – мощность является целой степенью двойки, но показатель степени c = 2 не совпадает с количеством компонент s = 3, претендующих быть внутренними (это первая, третья и четвертая компоненты). А = {010, 011, 001,000}: множество образует интервал, так как его мощность является целой степенью двойки (c=2), и эта степень совпадает с количеством компонент s=2, претендующих быть внутренними (это вторая и третья компоненты). Границы интервала: a = 000, b = 011. 7. Распознавание интервалов на матрице в коде Грея. Типы интервалов. Начало:задана матрица Грея с отмеченными клетками, которые образуют множество А. Шаг 1:Если число клеток множества А не являются целой степенью двойки, т.е. |А|¹2с, то А – не интервал, идем на конец. Шаг 2:Если множество А лежит симметрично относительно осей симметрии скомпонент (его можно «разрезрезать» осями на симметричные половины, затем четвертины на симметричные осьмушки и так далее до тех пор, пока множество А не «разрежется» на отдельные клетки), то А – интервал, идем на конец, иначе А не интервал. Конец. Примеры. На левой матрице задан интервал – 0 - - 1 (8 клеток и оси симметрии трех компонент), на правой – не интервал (4 клетки и ось симметрии лишь одной компоненты). Очевидно, что интервалами являются следующие множества: - каждая отдельная клетка, - любая пара симметричных клеток, в том числе радом лежащих, - любая строка и любой столбец, - любая пара симметричных строк и столбцов, в том числе рядом лежащих, - любой «квадрат» размером 2x2, - любая половина или четвертина матрицы, - четверка клеток, лежащих в углах матицы, - и не только они. Определение. Интервал Imax(f) назовем максимальным для булевой функции f (x1, x2, ..., xn), если он является допустимым для этой функции и не существует другого допустимого интервала I (f), такого что Imax(f) Ì I(f), другими словами, если после расширения интервала по любой компоненте он становится не допустимым. Пример. I1 (f) = - 1 1 — максимальный интервал, I2 (f) = 1 1 1— не максимальный.
8. Булева функция, способы ее задания. · Определение 1.Функцию f (x1, x2, ... , xn) называют булевой, если каждый ее аргумент есть булева переменная и сама функция — булева переменная. · Определение 2.Функцию f (x1, x2, ... , xn) называют булевой, если она сама и ее аргументы принимают значения 0 или 1. · Определение 3.Булевой функцией f (x1, x2, ... , xn) называют однозначное отображение булева пространства Bn в булево множество B, т.е. f: Bn® B. Пример. Рассмотрим булеву функцию двух аргументов, принимающую на наборах 01 и 10 значение 0, а на наборах 00 и 11 значение 1.
Способы задания булевых функций 1) Таблицей истинности.Так называется таблица, состоящая из двух частей: в левой части пересчитываются все наборы значений аргументов (булевы векторы пространства Bn) в естественном порядке, т.е. по возрастанию значений чисел, представляемых этими векторами, а в первой части – значений булевой функции на соответствующих наборах.
Теорема о числе булевых функций.Число различных булевых функций, зависящих от n переменных, равно 2) Характеристическими множествами.Так называются два множества: M1 (f), состоящее из всех наборов, на которых функция принимает значение 1, и M0 ( f ) — из всех наборов, на которых функция принимает значение 0, т.е. M1 (f) = {a Î B n : f (a) = 1}, M0 (f) = {a Î B n : f (a) = 0}. 3) Вектором значений функции:j(f) = f(0,0, ... ,0) f(0,0, ... ,1) ... f(1,1, ... ,1). 4) Матрицей Грея.Булево пространство задается матрицей Грея и наборами, на которых булева функция f(x1, x2, ... , xn) принимает значение 1, отмечаются и называются точками. Пример.
Пример: [Мажоритарная] функция может быть задана достаточным множеством If={I1,I2,I3} интервалов:
Здесь интервалы представлены троичными векторами и изображены на матрице Грея. В отличие от предыдущих, интервальный способ задания функций многовариантен. 6) Формулами. Пример.
9. Существенные и фиктивные переменные. Алгоритмы выявления и удаления фиктивной переменной. Булева функция f(x1, x2, ... , xi , ... , xn) существенно зависит от переменной xi, если выполняется условие: f (x1, x2, ... , xi -1, 0 , xi+1, ... , xn) ¹ f (x1, x2, ... , xi -1, 1 , xi+1, ... , xn). В этом случае также говорят, что переменная xi существенная, в противном случае ее называют фиктивной переменной. Пример. Рассмотрим булеву функцию f (x1, x2, x3) и исследуем ее переменные x1 и x3. Из таблиц истинности видно, что переменная x1 булевой функции f (x1, x2, x3) существенная, так как f (0, x2, x3) ¹ f (1, x2, x3). Переменная x3 фиктивная, так как f (x1, x2, 0) = f (x1, x2, 1).

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
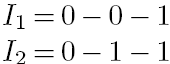 ранга 3 склеивания, образуя интервал I = 0 - - -1 ранга 2 (он является расширением интервалов I1 и I2 по третьей компоненте).
ранга 3 склеивания, образуя интервал I = 0 - - -1 ранга 2 (он является расширением интервалов I1 и I2 по третьей компоненте).



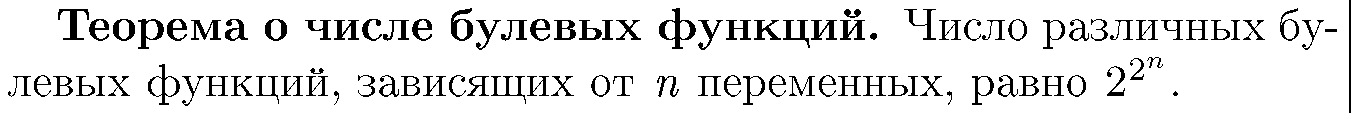 .
.


