|
|
Приложения алгебры логики.Кафедра ПОВТ и АС
Алгебра логики
Методические указания к практическим занятиям по курсу «Введение в математическую логику»
Ростов- на- Дону Составитель О.В. Ляхницкая,
Методические указания предназначены для студентов специальности 090102 «Компьютерная безопасность», 230105 «Программное обеспечение вычислительной техники и автоматизированных систем», 230102 «Автоматизированные системы управления» и преподавателей, ведущих практические занятия по курсу «Введение в математическую логику»; в них содержатся краткие сведения о логических операциях над высказываниями, равносильных формулах алгебры логики, рассматривается понятие двойственности, представлены алгоритмы приведения функций алгебры логики к СДНФ и СКНФ, а также приведены примеры применения алгебры логики в технике.
Рецензент:
Логические операции над высказываниями. 1. Отрицание. Отрицанием высказывания х называется новое высказывание
2. Конъюнкция (логическое умножение). Конъюнкцией двух высказываний х и у называется новое высказывание Таблица истинности операции конъюнкции имеет следующий вид:
3. Дизъюнкция (логическое сложение). Дизъюнкцией двух высказываний х и у называется новое высказывание Эту операцию наглядно можно изобразить с помощью таблицы истинности:
4. Импликация.Импликацией двух высказываний х и у называет новое высказывание Высказывание х называют посылкой, а у – заключением. Таблица истинности имеет следующий вид:
5. Эквиваленция.Эквиваленцией двух высказываний х и у называют новое высказывание Эту операцию наглядно можно изобразить с помощью таблицы истинности.
Символы Существуют операции, с помощью которых может быть выражена любая из пяти логических операций, рассмотренных выше. Такими операциями являются: 1. Штрих Шеффера (читается «А несовместно с В»). Эта операция обозначается
Имеет место следующее равенство 2. Стрелка Пирса(читается «ни А, ни В»). Эта операция обозначается
Имеет место следующее равенство 3. Сложение по модулю два (исключающее или). Эта операция обозначается
Имеет место следующее равенство 1. Составить таблицы истинности для формул: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16)
2. Выяснить, являются ли формулы тождественно истинными, тождественно ложными или выполнимыми: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) Равносильные формулы алгебры логики. Важнейшие равносильности алгебры логики можно разбить на 3 группы: 1. Основные равносильности:
2. Равносильности выражающие одни логические операции через другие:
3. Равносильности выражающие основные законы алгебры логики:
3. Доказать равносильности: а) построив таблицы истинности, б) используя основные равносильности 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 4. Используя основные равносильности алгебры логики докажите равносильность формул V и U: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) СДНФ, СКНФ. Пример 1. Пусть функция f(x1, x2, x3) задана таблицей истинности. Запишем ее в виде СДНФ.
Наборов, на которых функция равна 1, три: (0, 1, 0), (1, 0, 0) и (1, 1, 1), поэтому f(x1, x2, x3) = = Пример2. Пусть f(x1, x2, x3) = x1
Функция равна нулю только на наборе (1, 1, 0), поэтому f(x1 x2 x3)= Пример3:Следующую формулу привести к СДНФ, предварительно приведя её равносильными преобразованиями к ДНФ: А= Решение: Решение:
1) 2) 3) 4) 5) 6) 7) 6. Используя дистрибутивный закон перейти от заданной ДНФ формулы А к ее КНФ: 1) 2) 3) 4) 5) 6) 7) 8) 7. Привести к ДНФ( СДНФ), КНФ( СКНФ) следующие формулы: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16)
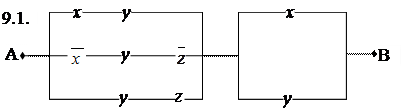
Приложения алгебры логики. 1. Приложения алгебра логики к релейно- контактным схем. 9. Найти функции проводимости следующих схем, если возможно упростить схемы:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , которое истинно тогда и только тогда, когда х ложно, и ложно, если высказывание х истинно.
, которое истинно тогда и только тогда, когда х ложно, и ложно, если высказывание х истинно. , которое считается истинным, если оба высказывания х и у истинны, и ложным во всех остальных случаях.
, которое считается истинным, если оба высказывания х и у истинны, и ложным во всех остальных случаях. , которое считается ложным, если оба высказывания х и у ложны, и истинным во всех остальных случаях.
, которое считается ложным, если оба высказывания х и у ложны, и истинным во всех остальных случаях.
 , которое считается ложным, если х- истинно, а у- ложно, и истинным во всех остальных случаях.
, которое считается ложным, если х- истинно, а у- ложно, и истинным во всех остальных случаях. , которое считается истинным, когда оба высказывания х и у либо одновременно истинны, либо одновременно ложны..
, которое считается истинным, когда оба высказывания х и у либо одновременно истинны, либо одновременно ложны..
 называются позиционными связками. Логическим связкам приписывают ранги в следующем порядке убывания старшинства:
называются позиционными связками. Логическим связкам приписывают ранги в следующем порядке убывания старшинства:  и определяется следующей таблицей истинности.
и определяется следующей таблицей истинности.

 и определяется следующей таблицей истинности.
и определяется следующей таблицей истинности.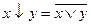
 и определяется следующей таблицей истинности.
и определяется следующей таблицей истинности.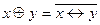
 ;
;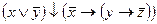 ;
;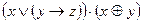 ;
; ;
;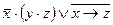 ;
; ;
; ;
; ;
;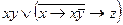 ;
; ;
; ;
; ;
;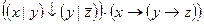 ;
; ;
; ;
;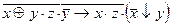 .
.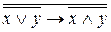



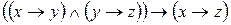



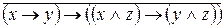

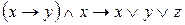



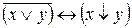


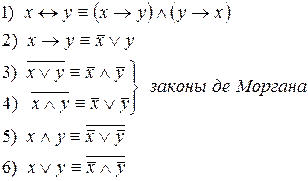

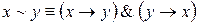 ;
;
 ;
;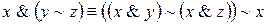 ;
; ;
; ;
;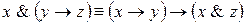 ;
; ;
; ;
;




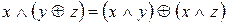
 .
.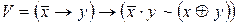 ,
,  ;
; ,
,  ;
; ,
, 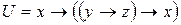 ;
; ,
, 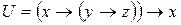 ;
;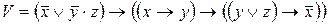 ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
;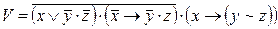 ,
,  ;
; ,
, 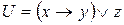 .
. ,
, 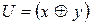
 ,
, 
 ,
, 





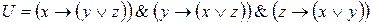
 &x2&
&x2&  Úx1&
Úx1&  &
&  (x2
(x2 
 Пример4: Следующую формулу привести к СКНФ, предварительно приведя её равносильными преобразованиями к КНФ: А=
Пример4: Следующую формулу привести к СКНФ, предварительно приведя её равносильными преобразованиями к КНФ: А= 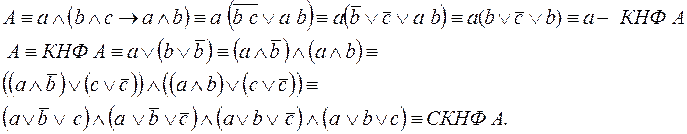 5. Используя дистрибутивный закон перейти от заданной КНФ формулы А к ДНФ:
5. Используя дистрибутивный закон перейти от заданной КНФ формулы А к ДНФ:





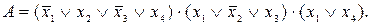
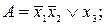
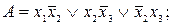







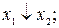
 ;
;

 ;
; ;
; ;
; ;
;
 ;
; ;
; ;
; ;
;