ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- ПОНЯТИЕ О ДИФФЕРЕНЦИАЛЬНОМ УРАВНЕНИИ
Обыкновенным дифференциальным уравнением n – го порядка называют уравнения вида
 (1.1) (1.1)
где  - искомая функция. Любая функция - искомая функция. Любая функция  обращающая уравнение (1.1) в тождество, называется решением этого уравнения, а график этой функции – интегральной кривой. Если решение задано в неявном виде обращающая уравнение (1.1) в тождество, называется решением этого уравнения, а график этой функции – интегральной кривой. Если решение задано в неявном виде  , то оно обычно называется интегралом уравнения (1.1). , то оно обычно называется интегралом уравнения (1.1).
Функция  содержащая содержащая  независимых произвольных постоянных, называется общим решением уравнения (1.1), если она называется его решением при любых значениях постоянных независимых произвольных постоянных, называется общим решением уравнения (1.1), если она называется его решением при любых значениях постоянных  . Если эта функция задается в неявном виде выражением . Если эта функция задается в неявном виде выражением  то это выражение называется общим интегралом уравнения (1.1). Придавая в выражении постоянным то это выражение называется общим интегралом уравнения (1.1). Придавая в выражении постоянным  определенные выражения постоянным определенные выражения постоянным  получаем частное решение или соответственно частный интеграл уравнения (1.1). получаем частное решение или соответственно частный интеграл уравнения (1.1).
Обратно, имея семейство кривых, задаваемых уравнением  и исключая параметры и исключая параметры  из системы уравнений из системы уравнений
 , , 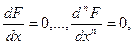
получим, вообще говоря, дифференциальное уравнение вида (1.1) для которого  является общим интегралом. является общим интегралом.
Дифференциальное уравнение первого порядка имеет вид
 (1.2) (1.2)
решив уравнение (1.2) относительно  если это возможно, получим если это возможно, получим
 (1.3) (1.3)
Уравнение (1.3) определяет наклон  интегральной кривой в точке интегральной кривой в точке  т.е. определяет поле направлений интегральных кривых. т.е. определяет поле направлений интегральных кривых.
Если в некоторой области функция  непрерывна и имеет ограниченную частную производную непрерывна и имеет ограниченную частную производную  , то оказывается, что через каждую внутреннюю точку , то оказывается, что через каждую внутреннюю точку  этой области пройдет единственная интегральная кривая. этой области пройдет единственная интегральная кривая.
В такой области уравнение (1.3) имеет общее решение  или общий интеграл или общий интеграл  , из которого можно найти единственное частное решение, или единственный частный интеграл, удовлетворяющий начальным условиям: , из которого можно найти единственное частное решение, или единственный частный интеграл, удовлетворяющий начальным условиям:  при при  . .
- ДИФФЕРЕНЦИАЛЬОЕ УРАВНЕНИЕ ПЕРВОГО ПОРЯДКА С
РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ.
ОРТОГОНАЛЬНЫЕ ТРАЕКТОРИИ
Дифференциальное уравнение первого порядка
 (2.1) (2.1)
где  и и  - функции - функции  и и  , называется уравнением с разделяющимися переменными, если коэффициенты , называется уравнением с разделяющимися переменными, если коэффициенты  и и  при дифференциалах разлагаются на множители, зависящие только от при дифференциалах разлагаются на множители, зависящие только от  или только от или только от  , т.е. если оно имеет вид , т.е. если оно имеет вид
 (2.2) (2.2)
Разделив оба члена уравнения (2.2) на  получим получим
 (2.3) (2.3)
Общим интегралом уравнения (2.3), а следовательно и (2.2), будет
 (2.4) (2.4)
Ортогональные траектории семейства линий  называются линии, пересекающие линии одного семейства под прямым углом. Продифференцировав уравнение называются линии, пересекающие линии одного семейства под прямым углом. Продифференцировав уравнение  по по  и исключив и исключив 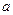 из полученного и данного уравнений получим дифференциальное уравнение линий данного семейства из полученного и данного уравнений получим дифференциальное уравнение линий данного семейства  Тогда дифференциальным уравнением ортогональных траекторий будет: Тогда дифференциальным уравнением ортогональных траекторий будет:

- ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА:
ОДНОРОДНОЕ, 2) ЛИНЕЙНОЕ, 3) БЕРНУЛЛИ
Однородное уравнение. 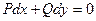 называется однородным, если называется однородным, если  и и  - однородные функции от - однородные функции от  и и  одинакового измерения. Оно приводится к виду одинакового измерения. Оно приводится к виду  и решается подстановкой и решается подстановкой  или или 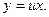
Линейное уравнение. Дифференциальное уравнение называется линейным, если оно первой степени относительно искомой функции  и всех ее производных. и всех ее производных.
Линейное уравнение первого порядка имеет вид  . Оно сводится к двум уравнениям с разделяющимися переменными подстановкой . Оно сводится к двум уравнениям с разделяющимися переменными подстановкой  . Другой способ решения (вариация произвольной постоянной) состоит в том, что сначала решаем уравнение . Другой способ решения (вариация произвольной постоянной) состоит в том, что сначала решаем уравнение  ; получаем ; получаем  Подставляем это решение в данное уравнение, считая Подставляем это решение в данное уравнение, считая  функцией функцией  , и затем находим , и затем находим  и и  . .
Уравнение Бернулли  решается также, как и линейное, подстановкой решается также, как и линейное, подстановкой  или вариации произвольной постоянной. Уравнение Бернулли приводится к линейному подстановкой или вариации произвольной постоянной. Уравнение Бернулли приводится к линейному подстановкой  . .
- ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, СОДЕРЖАЩИЕ ДИФФЕРЕНЦИАЛЫ
ПРОИЗВЕДЕНИЯ И ЧАСТНОГО
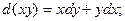
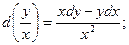
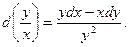
Такие уравнения иногда легко решаются, если соответственно положить  , ,  или или   . .
- ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ПЕРВОГО ПОРЯДКА В ПОЛНЫХ
ДИФФЕРЕНЦИАЛАХ. ИНТЕГРИРУЮЩИЙ МНОЖИТЕЛЬ
Если в дифференциальном уравнении
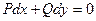
 , то оно приобретает вид , то оно приобретает вид  и его общий интеграл будет и его общий интеграл будет  . .
Если  , то при некоторых условиях существует функция , то при некоторых условиях существует функция  , такая, что , такая, что  Эта функция Эта функция  называется интегрирующим множителем. называется интегрирующим множителем.
Интегрирующий множитель легко найти в случаях:
1) когда  , когда , когда 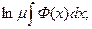
2) когда  , когда , когда 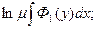
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


 (1.1)
(1.1) - искомая функция. Любая функция
- искомая функция. Любая функция  обращающая уравнение (1.1) в тождество, называется решением этого уравнения, а график этой функции – интегральной кривой. Если решение задано в неявном виде
обращающая уравнение (1.1) в тождество, называется решением этого уравнения, а график этой функции – интегральной кривой. Если решение задано в неявном виде  , то оно обычно называется интегралом уравнения (1.1).
, то оно обычно называется интегралом уравнения (1.1). содержащая
содержащая  независимых произвольных постоянных, называется общим решением уравнения (1.1), если она называется его решением при любых значениях постоянных
независимых произвольных постоянных, называется общим решением уравнения (1.1), если она называется его решением при любых значениях постоянных  . Если эта функция задается в неявном виде выражением
. Если эта функция задается в неявном виде выражением  то это выражение называется общим интегралом уравнения (1.1). Придавая в выражении постоянным
то это выражение называется общим интегралом уравнения (1.1). Придавая в выражении постоянным  определенные выражения постоянным
определенные выражения постоянным  получаем частное решение или соответственно частный интеграл уравнения (1.1).
получаем частное решение или соответственно частный интеграл уравнения (1.1). ,
, 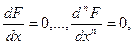
 (1.2)
(1.2) если это возможно, получим
если это возможно, получим (1.3)
(1.3) интегральной кривой в точке
интегральной кривой в точке  т.е. определяет поле направлений интегральных кривых.
т.е. определяет поле направлений интегральных кривых. непрерывна и имеет ограниченную частную производную
непрерывна и имеет ограниченную частную производную  , то оказывается, что через каждую внутреннюю точку
, то оказывается, что через каждую внутреннюю точку  этой области пройдет единственная интегральная кривая.
этой области пройдет единственная интегральная кривая. или общий интеграл
или общий интеграл  , из которого можно найти единственное частное решение, или единственный частный интеграл, удовлетворяющий начальным условиям:
, из которого можно найти единственное частное решение, или единственный частный интеграл, удовлетворяющий начальным условиям:  при
при  .
. (2.1)
(2.1) и
и  - функции
- функции  и
и  , называется уравнением с разделяющимися переменными, если коэффициенты
, называется уравнением с разделяющимися переменными, если коэффициенты  (2.2)
(2.2) получим
получим (2.3)
(2.3) (2.4)
(2.4) называются линии, пересекающие линии одного семейства под прямым углом. Продифференцировав уравнение
называются линии, пересекающие линии одного семейства под прямым углом. Продифференцировав уравнение 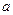 из полученного и данного уравнений получим дифференциальное уравнение линий данного семейства
из полученного и данного уравнений получим дифференциальное уравнение линий данного семейства  Тогда дифференциальным уравнением ортогональных траекторий будет:
Тогда дифференциальным уравнением ортогональных траекторий будет:
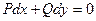 называется однородным, если
называется однородным, если  и решается подстановкой
и решается подстановкой  или
или 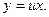
 . Оно сводится к двум уравнениям с разделяющимися переменными подстановкой
. Оно сводится к двум уравнениям с разделяющимися переменными подстановкой  . Другой способ решения (вариация произвольной постоянной) состоит в том, что сначала решаем уравнение
. Другой способ решения (вариация произвольной постоянной) состоит в том, что сначала решаем уравнение  ; получаем
; получаем  Подставляем это решение в данное уравнение, считая
Подставляем это решение в данное уравнение, считая  функцией
функцией  и
и  решается также, как и линейное, подстановкой
решается также, как и линейное, подстановкой  .
.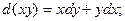
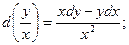
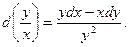
 ,
,  или
или 
 .
. , то оно приобретает вид
, то оно приобретает вид  и его общий интеграл будет
и его общий интеграл будет  .
. , то при некоторых условиях существует функция
, то при некоторых условиях существует функция  , такая, что
, такая, что  Эта функция
Эта функция  , когда
, когда 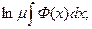
 , когда
, когда