
|
|
Собственные числа и собственные вектораДля анализа внутренней структуры линейного преобразования целесообразно найти вектора, которые данное преобразование изменяет наиболее просто. Таким свойством обладают собственные вектора матрицы, удовлетворяющие соотношению
где l - коэффициент, показывающий изменения длины вектора, т.е. образ вектора совпадает с прообразом по направлению и отличается от него лишь длиной. Умножим представленное соотношение слева на единичную матрицу E и перенесем все члены в левую часть.
Матрица
Для вычисления вектора Для того чтобы найти значение числа l, при котором определитель
Известно, что решением уравнения степени nявляется n значений Пусть в качестве базиса принята совокупность собственных векторов
Если собственные числа li различны, то собственные вектора Таким образом, в базисе из линейно-независимых собственных векторов матрица линейного преобразования преобразует вектор путем растяжения, сжатия или разворота (l<0) координат вектора (умножение проекций на соответствующие собственные числа). Пример: Найти собственные числа и собственные вектора матрицы Характеристическая матрица
Приравнивая нулю определитель матрицы
Вычисление собственных векторов. Первый собственный вектор
Последнее матричное уравнение эквивалентно системе:
Нетрудно видеть, что уравнения линейно-зависимы, следовательно, любое из них, например второе, можно удалить. Тогда
Отбрасываем второе уравнение, задав
Найденные вектора представлены на рис. 7.7.
Т.к. матрица А симметрична, то исходный ортонормированный базис преобразуется в ортогональный (можно сделать ортонормированным, поделив каждый вектор нового базиса на его длину). Рассмотрим некоторый вектор
В результате получаем вектор большей длины, расположенный под углом с исходным вектором Тот же вектор
Если взять множество векторов, лежащих концами на единичной окружности, то матрица линейного преобразования будет в 3 раза вытягивать проекции на вектор Преобразование подобия Совокупность линейно-независимых собственных векторов образует базис. При этом матрица перехода из исходного базиса в новый представляется совокупностью координат собственных векторов в исходном базисе
Соотношения
где Нельзя писать
в то время как умножение на диагональную матрицу слева равносильно умножению на коэффициенты
Умножив уравнение (7.8) сначала справа, а затем слева на матрицу
МатрицыАи L представляют собой одно и то же линейное преобразование, записанное в различных системах координат. Матрица А показывает преобразование в координатах базиса Итак, одному и тому же линейному преобразованию в разных базисах соответствует отличающиеся матрицы. Базис1: Базис 2: Базис 3: где B= Матрицы А и L называются подобными, т.к. соответствуют одному и тому же преобразованию. Определители этих матриц равны. Отсюда определитель матрицы равен произведению всех его собственных чисел
С помощью данной диаграммы легко получается соотношение подобия (7.9), которое показывает переход от вектора Норма матрицы Первое (максимальное) собственное число Норма матрицы является одной из характеристик матрицы. Поскольку матрица является отражением некоторого линейного преобразования, то неудивительно, что норма матрицы теоретически определяется через линейное преобразование верхней границей изменения длины вектора (представленный ниже оператор sup обозначает точную верхнюю границу)
т.е. норма матрицы характеризуется максимальным по модулю образом единичного вектора. Отсюда понятно соотношение Используются три способа вычисления нормы матрицы. 1. Кубическая норма (норма по строкам) равна максимальной сумме модулей элементов строк 2. Октаэдрическая норма (норма по столбцам) равна максимальной сумме модулей элементов столбцов, 3. Сферическая норма (Евклидова норма). Свойства норм матрицы:
Для любой симметричной матрицы Сжимающее отображение Преобразование (отображение) называется сжимающим, если Для оценки
В правой части записано представление прообраза вектора через его образ. Поскольку матрице А-1 соответствует матрица 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
,
 называется характеристической матрицей. Очевидно, что она имеет вид:
называется характеристической матрицей. Очевидно, что она имеет вид:
 нужно решить систему
нужно решить систему 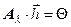 . Эта система однородна (в правой части стоит нулевой вектор) и имеет ненулевое решение
. Эта система однородна (в правой части стоит нулевой вектор) и имеет ненулевое решение  только тогда, когда определитель матрицы
только тогда, когда определитель матрицы 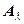 равен нулю (
равен нулю (  ). В этом случае в матрице
). В этом случае в матрице  .
. обратился в ноль, нужно аналитически выписать определитель матрицы, приводя подобные члены относительно степеней l. В общем случае для матрицы размерностью nполучим характеристическое уравнение степени n:
обратился в ноль, нужно аналитически выписать определитель матрицы, приводя подобные члены относительно степеней l. В общем случае для матрицы размерностью nполучим характеристическое уравнение степени n: .
.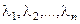 . Числа li называются собственными числами (значениями) матрицы. Обычно li располагают в ряд по уменьшению модуля, при этом максимальное значение обозначают через l1 , а минимальное через ln .
. Числа li называются собственными числами (значениями) матрицы. Обычно li располагают в ряд по уменьшению модуля, при этом максимальное значение обозначают через l1 , а минимальное через ln . и вектор
и вектор  имеет в этой системе координаты
имеет в этой системе координаты  ,
,  . Тогда
. Тогда  . Поскольку
. Поскольку  то
то  , т.е. при линейном преобразовании координаты вектора по величине сокращаются (li < 1) или удлиняются (li > 1) пропорционально собственным числам. Линейное преобразование
, т.е. при линейном преобразовании координаты вектора по величине сокращаются (li < 1) или удлиняются (li > 1) пропорционально собственным числам. Линейное преобразование  в базисе собственных векторов
в базисе собственных векторов  .
. линейно-независимы. Отметим, что если
линейно-независимы. Отметим, что если  также будет собственным вектором, т.е. для каждого li имеется не один собственный вектор, а бесчисленное множество векторов, лежащих на одном и том же направлении.
также будет собственным вектором, т.е. для каждого li имеется не один собственный вектор, а бесчисленное множество векторов, лежащих на одном и том же направлении. .
. имеет вид
имеет вид
 . Отсюда
. Отсюда  .
. может быть найден из уравнения
может быть найден из уравнения  , или
, или .
. .
. . Задавая
. Задавая  , получим
, получим 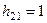 . Отсюда вектор
. Отсюда вектор  .
. Уравнение
Уравнение  для второго собственного вектора приводит к системе:
для второго собственного вектора приводит к системе: 
 , получим
, получим  , т.е.
, т.е.  .
.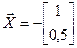 и найдем его образ
и найдем его образ  под действием матрицы
под действием матрицы  :
:
 (числа a и b). Линейное преобразование заключается в умножении первой проекции (a) на первое собственное число
(числа a и b). Линейное преобразование заключается в умножении первой проекции (a) на первое собственное число  , и второй проекции
, и второй проекции  на величину
на величину  . Геометрически складывая преобразованные проекции (OD и DE), получаем тот же вектор
. Геометрически складывая преобразованные проекции (OD и DE), получаем тот же вектор  .
.

 .
. в матричном виде можно представить как
в матричном виде можно представить как ,
,
 - диагональная матрица из собственных чисел:
- диагональная матрица из собственных чисел:  .
. , так как
, так как  , что не соответствует действительности, и, кроме того, при умножении матрицы H на
, что не соответствует действительности, и, кроме того, при умножении матрицы H на  ,
, строк, а не столбцов, что противоречит математическому смыслу собственных векторов:
строк, а не столбцов, что противоречит математическому смыслу собственных векторов: .
.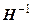 , получим
, получим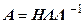 ;
;  .
.
 , а матрица L показывает тоже преобразование в координатах базиса
, а матрица L показывает тоже преобразование в координатах базиса 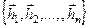 .
. ,
, 

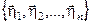 –
– 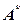 ,
,  ,
, , (см.п.7.2)
, (см.п.7.2) .
. Структурная диаграмма преобразования векторов представлена на рис. 7.9. В частности, если требуется преобразовать вектор из базиса
Структурная диаграмма преобразования векторов представлена на рис. 7.9. В частности, если требуется преобразовать вектор из базиса  в базис
в базис  , то необходимо умножить его на матрицу H-1.
, то необходимо умножить его на матрицу H-1. к его образу
к его образу 
 по и против часовой стрелки.
по и против часовой стрелки. характеризует максимальное растяжение (при
характеризует максимальное растяжение (при  ,
,  .
. ,
,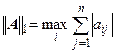 ,.
,. .
. .
.
 .
. . Это справедливо при
. Это справедливо при  или
или  .
. , характеризующего максимальную степень сжатия, необходимо отметить, что переход от образа к прообразу связан с матрицей А-1.
, характеризующего максимальную степень сжатия, необходимо отметить, что переход от образа к прообразу связан с матрицей А-1.
 .
. , то
, то  - максимальное собственное число
- максимальное собственное число  для обратной матрицы А-1 и
для обратной матрицы А-1 и  .
.