Доказательство на основе понятия расстояния от вектора до подпространства
Рассмотрим матрицу, построенную на векторах 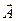 = =  , , 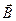 = =  . Объем фигуры (параллелограмма), построенной на данных векторах определяется произведением модуля вектора . Объем фигуры (параллелограмма), построенной на данных векторах определяется произведением модуля вектора 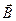 (объемфигуры векторного подпространства R1 меньшей размерности) на высоту h (минимальное расстояние от вектора (объемфигуры векторного подпространства R1 меньшей размерности) на высоту h (минимальное расстояние от вектора 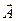 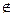 R1 до подпространства R1, образованного вектором R1 до подпространства R1, образованного вектором 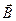 . .
В подпространстве R1 найдется такой вектор 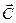 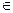 R1, которому соответствует разность R1, которому соответствует разность 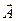 - - 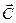 , модуль которой определяет высоту h. В свою очередь, вектор , модуль которой определяет высоту h. В свою очередь, вектор 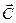 является, во-первых частью является, во-первых частью 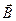 , , 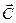 =λ =λ 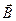 , а, во-вторых,проекцией , а, во-вторых,проекцией 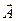 на на 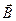
Исходя из определения скалярного произведения можно записать
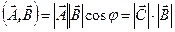 . .
Отсюда
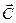 = = 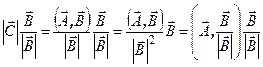
| (7.4)
| В последнем выражении второй сомножитель является единичным вектором, направленным вдоль вектора 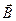 , и служит для преобразования скалярной величины (проекция) в векторную. Так как , и служит для преобразования скалярной величины (проекция) в векторную. Так как 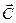 =λ =λ 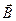 , то , то
 , ,
| (7.5)
| а квадрат расстояния от 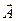 до подпространства, образованного вектором до подпространства, образованного вектором 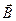
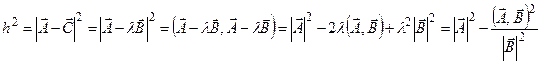 . .
| (7.6)
| При этом квадрат объема параллелепипеда
 . .
| (7.7)
| Подставляя координаты векторов, получаем
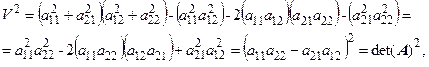 . .
что и требовалось доказать. Доказательство идентичности детерминанта матрицы и объема параллелепипеда на пространстве большей размерности выполняется по индукции, но в силу громоздкости доказательства оно здесь не приводится.
Оптимальное значение коэффициента λ (7.5), соответствующее вектору 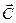 можно получить, решая оптимизационную задачу. можно получить, решая оптимизационную задачу.
Минимальное расстояние от вектора 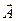 до подпространства R1 определяется параметром λ из условия h=| до подпространства R1 определяется параметром λ из условия h=| 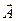 -λ -λ 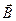 ,|, ,|, 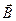 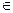 R1 R1  . Поскольку модуль числа всегда положителен, то это эквивалентно . Поскольку модуль числа всегда положителен, то это эквивалентно  . Дифференцируя данное выражение по λ и приравнивая результат к нулю, получаем . Дифференцируя данное выражение по λ и приравнивая результат к нулю, получаем
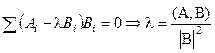 , что совпадает с (7.5). , что совпадает с (7.5).
Доказательство(7.7)на основе формулы площади параллелограмма
Высота h в параллелограмме определяется выражением 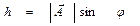 . При этом . При этом
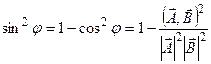 . .
Отсюда  , что совпадает с (7.7). , что совпадает с (7.7).
Ортогональность столбцов матрицы А
Если столбцы матрицы А ортогональны, то их попарные скалярные произведение равны нулю. При этом для прямоугольного параллелепипеда
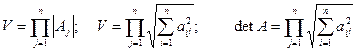
Ортонормированность базиса
Математические операции в ортонормированном базисе значительно проще за счет того, что скалярное произведение любых двух векторов базиса равно нулю, а длина каждого вектора равна единице. При этом коэффициенты разложения вектора в упомянутом базисе равны проекциям (скалярному произведению) вектора на единичный орт.
Аппарат минимальных расстояний позволяет выполнить ортогонализацию и нормализацию произвольного базиса. Пусть имеется базис 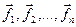 . .
В качестве первого вектора ортонормированного базиса выбирается вектор  . Вторым вектором является нормированный вектор . Вторым вектором является нормированный вектор  , определяющий минимальное расстояние от , определяющий минимальное расстояние от 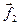 до до  , ,  . Подобно (7.5) определяется коэффициент λ. Отсюда вектор . Подобно (7.5) определяется коэффициент λ. Отсюда вектор 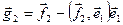 . Аналогично, . Аналогично,  , где , где 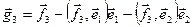 , т.е. , т.е. 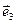 определяется минимальным расстоянием до подпространства, порожденного векторами определяется минимальным расстоянием до подпространства, порожденного векторами  с ортонормированным базисом с ортонормированным базисом  . Распространяя данную процедуру, получаем . Распространяя данную процедуру, получаем 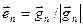 , где , где 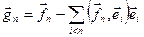 . .
Очевидно, что если 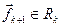 , то , то  , ,  . Это замечание делает понятным геометрический смысл особенностей матриц и линейных преобразований с определителем, равным нулю. Если матрица Аимеет определитель, равный нулю, то преобразование, соответствующее матрице А, переводит вектора исходного пространства в вектора подпространства меньшей размерности. В самом деле, поскольку определитель равен по модулю объему параллелепипеда, построенного на образах единичных координатных векторов, то в случае det A = 0 расстояние от конца хотя бы одного вектора . Это замечание делает понятным геометрический смысл особенностей матриц и линейных преобразований с определителем, равным нулю. Если матрица Аимеет определитель, равный нулю, то преобразование, соответствующее матрице А, переводит вектора исходного пространства в вектора подпространства меньшей размерности. В самом деле, поскольку определитель равен по модулю объему параллелепипеда, построенного на образах единичных координатных векторов, то в случае det A = 0 расстояние от конца хотя бы одного вектора  до подпространства предыдущих векторов до подпространства предыдущих векторов  равно нулю. Следовательно, равно нулю. Следовательно,  принадлежит подпространству i-1векторов. А это в свою очередь означает, что пространство образов имеет уже не n независимых векторов, а меньшее количество и является подпространством исходного пространства. принадлежит подпространству i-1векторов. А это в свою очередь означает, что пространство образов имеет уже не n независимых векторов, а меньшее количество и является подпространством исходного пространства.
 Пример. Выполнить ортогонализацию векторов Пример. Выполнить ортогонализацию векторов   . .
| Рис. 7.6. Ортогонализация
| Первый вектор нового базиса 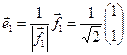 . Перпендикулярный . Перпендикулярный 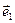 вектор вектор  . .
Второй нормированный вектор нового базиса
 . .
Новый ортонормированный базис представлен на рис. 7.6.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


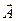 =
=  ,
, 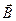 =
=  . Объем фигуры (параллелограмма), построенной на данных векторах определяется произведением модуля вектора
. Объем фигуры (параллелограмма), построенной на данных векторах определяется произведением модуля вектора 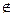 R1 до подпространства R1, образованного вектором
R1 до подпространства R1, образованного вектором 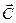
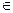 R1, которому соответствует разность
R1, которому соответствует разность 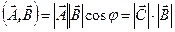 .
.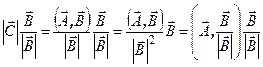
 ,
,
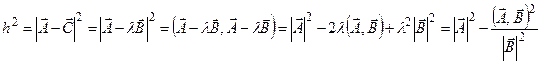 .
.
 .
.
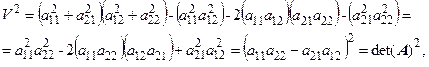 .
. . Поскольку модуль числа всегда положителен, то это эквивалентно
. Поскольку модуль числа всегда положителен, то это эквивалентно  . Дифференцируя данное выражение по λ и приравнивая результат к нулю, получаем
. Дифференцируя данное выражение по λ и приравнивая результат к нулю, получаем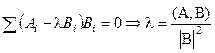 , что совпадает с (7.5).
, что совпадает с (7.5).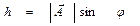 . При этом
. При этом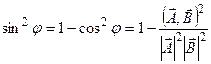 .
. , что совпадает с (7.7).
, что совпадает с (7.7).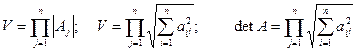
 .
. . Вторым вектором является нормированный вектор
. Вторым вектором является нормированный вектор  , определяющий минимальное расстояние от
, определяющий минимальное расстояние от 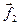 до
до  ,
,  . Подобно (7.5) определяется коэффициент λ. Отсюда вектор
. Подобно (7.5) определяется коэффициент λ. Отсюда вектор 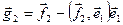 . Аналогично,
. Аналогично,  , где
, где 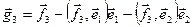 , т.е.
, т.е. 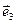 определяется минимальным расстоянием до подпространства, порожденного векторами
определяется минимальным расстоянием до подпространства, порожденного векторами  с ортонормированным базисом
с ортонормированным базисом  . Распространяя данную процедуру, получаем
. Распространяя данную процедуру, получаем 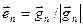 , где
, где 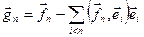 .
.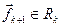 , то
, то  ,
,  . Это замечание делает понятным геометрический смысл особенностей матриц и линейных преобразований с определителем, равным нулю. Если матрица Аимеет определитель, равный нулю, то преобразование, соответствующее матрице А, переводит вектора исходного пространства в вектора подпространства меньшей размерности. В самом деле, поскольку определитель равен по модулю объему параллелепипеда, построенного на образах единичных координатных векторов, то в случае det A = 0 расстояние от конца хотя бы одного вектора
. Это замечание делает понятным геометрический смысл особенностей матриц и линейных преобразований с определителем, равным нулю. Если матрица Аимеет определитель, равный нулю, то преобразование, соответствующее матрице А, переводит вектора исходного пространства в вектора подпространства меньшей размерности. В самом деле, поскольку определитель равен по модулю объему параллелепипеда, построенного на образах единичных координатных векторов, то в случае det A = 0 расстояние от конца хотя бы одного вектора  до подпространства предыдущих векторов
до подпространства предыдущих векторов  равно нулю. Следовательно,
равно нулю. Следовательно,  принадлежит подпространству i-1векторов. А это в свою очередь означает, что пространство образов имеет уже не n независимых векторов, а меньшее количество и является подпространством исходного пространства.
принадлежит подпространству i-1векторов. А это в свою очередь означает, что пространство образов имеет уже не n независимых векторов, а меньшее количество и является подпространством исходного пространства. Пример. Выполнить ортогонализацию векторов
Пример. Выполнить ортогонализацию векторов 
 .
.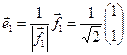 . Перпендикулярный
. Перпендикулярный 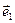 вектор
вектор  .
. .
.